Опыт использования нейронных сетей в анализе и структурном воссоздании предметных знаний специалиста

Разработка автоматизированной обучающей системы (АОС) представляет собой сложный и трудоемкий процесс. Любая АОС — это система, основанная на знаниях и обрабатывающая знания. База знаний обучающей системы в первую очередь должна содержать предметные знания. Свойство адаптивности АОС во многом определяется способами структурирования учебного материала (УМ). Чем больше у системы возможностей обеспечить пользователю индивидуальный маршрут изучения УМ, тем более гибким и адаптивным является ее поведение. Таким образом, вопросы структурирования, представления и доступа к знаниям являются центральными при разработке современной АОС [1].

Важным шагом на пути выявления структуры, присущей знаниям, является построение моделей, в которых в явной форме выделены объекты, образующие эту структуру [2, 3]. В основе этих моделей лежит понятие сети, состоящей из вершин, или узлов, соединенных дугами. С вершинами этой сети сопоставляются понятия (объекты, события, процессы, явления и др.), а с дугами — связи, или отношения, существующие между этими понятиями. Графическое исполнение элементов сети произвольное. Объекты могут изображаться точками, кружками, прямоугольниками и другими способами, дуги могут быть прямыми, ломаными, кривыми линиями. Семантические сети (СС), с одной стороны, имитируют естествен- ное понимание языка человеком, а с другой стороны, придают фактическим знаниям графовую структурированную организацию, они представляют собой так называемые ориентированные графы [4, 5, 6]. Построение СС как графа способствует процессу осмысления знаний, способствует их конкретизации, выявлению противоречий, обнаружению недостающей информации и т. п. Вначале СС использовались в психологии для моделирования долговременной памяти человека и только затем они перешли в инженерию знаний в качестве одного из основных методов представления знаний в АОС. В качестве понятий семантической сети обычно выступают абстрактные или конкретные объекты. Отношения могут быть самого разного типа, что позволяет в достаточной мере обеспечить в СС такой признак знаний, как связность. Семантические сети легко передают как отношения "абстрактное—конкретное", так и "целое—часть".

НАВИГАЦИОННЫЙ ТРЕУГОЛЬНИК СКОРОСТЕЙ

Рассмотрим, как с помощью СС представить систему знаний по параграфу "Навигационный треугольник скоростей" главы "Учет влияния ветра на полет летательного аппарата" учебного пособия для штурмана [13]. Навигационный треугольник скоростей (НТС), рис. 1, — треугольник, образованный векторами воздушной V , путевой W

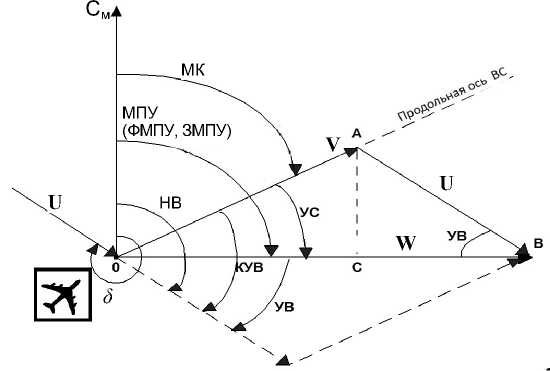
Рис. 1. Навигационный треугольник скоростей и его элементы.

Обозначены:

См — северное направление магнитного меридиана; МК — магнитный курс; МПУ — магнитный путевой угол; НВ — направление ветра; КУВ — курсовой угол ветра; УВ — угол ветра; УС — угол сноса; V — воздушная скорость; W — путевая скорость; U — скорость ветра скоростей воздушного судна (ВС) и скорости ветра U при полете с боковой составляющей ветра.

В состав НТС (рис. 1) входят следующие элементы:

МК — магнитный курс ВС;

V — воздушная скорость;

МПУ — магнитный путевой угол (может быть заданным ЗМПУ и фактическим ФМПУ);

W — путевая скорость;

НВ — навигационное направление ветра;

U — скорость ветра;

УС — угол сноса;

УВ — угол ветра [7].

Зависимости, существующие между элементами НТС, имеют следующий вид:

МК = ЗМПУ – (±УС);

УВ = δ ± 180° – ЗМПУ;

ФМПУ = МК + (±УС);

КУВ = УВ + (± УС);

УС = ФМПУ – МК;

δ = ФМПУ + УВ ± 180°;

W = V cos(УС) + U cos(УВ).

ПОСТРОЕНИЕ СЕМАНТИЧЕСКОГО ГРАФА

На базе изложенного УМ строится семантический граф (СГ), вершинами которого являются понятия предметной области (ПрО) — учебные элементы (УЭ), а дугами — их отношения и взаимосвязи (рис. 2).

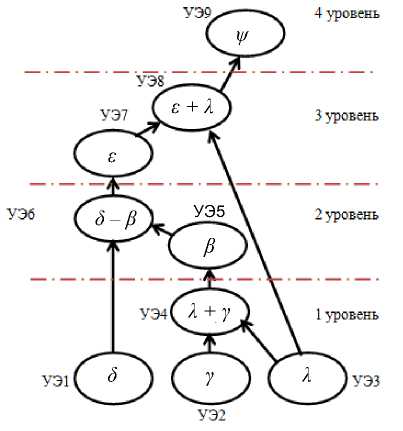
Рис. 2. Семантический граф навигационного треугольника скоростей.

Обозначены элементы:

УЭ1 — δ (метеорологическое направление ветра); УЭ2 — γ (курс полета МК); УЭ3 — λ (угол сноса УС); УЭ4 — ( λ + γ ); УЭ5 — β (путевой угол МПУ); УЭ6 — ( δ – β ); УЭ7 — ε (угол ветра УВ); УЭ8 — ( ε + λ ); УЭ9 — ψ (курсовой угол ветра КУВ)

На рис. 2 введены следующие обозначения: УЭ1 — δ (метеорологическое направление вет-		элементов а ij . Размер матрицы равен количеству УЭ — в нашем случае і , j = 9. Все элементы мат-
ра),		рицы принимают бинарные значения — (1 или 0).
УЭ2 — γ (курс полета МК),		Единица характеризует наличие связи (однона-
УЭ3 — λ (угол сноса УС),		правленной или двунаправленной) между		УЭ,
УЭ4 — ( λ + γ ),		ноль — отсутствие связи между УЭ. Например
УЭ5 — β (путевой угол МПУ),		УЭ1 связан с УЭ6 (рис. 2), и поэтому эту связь ха-
УЭ6 — ( δ – β ),		рактеризуют элемент а 1,6 матрицы А . Элемент а 1,6
УЭ7 — ε (угол ветра УВ),		располагается на пересечении строки с номером
УЭ8 — ( ε + λ ),		i = 1 и столбца	с номером j = 6 матрицы А . Так
УЭ9 — ψ (курсовой угол ветра КУВ).		как УЭ1 и УЭ6 связаны, то элемент а 1,6 = 1.		Мат-
Граф, приведенный на рис. 2, можно предста-		рица, соответствующая СГ рис. 2, представлена ГП-
вить	в виде квадратной матрицы А , состоящей из
	" 0 0 0    0       0    УЭ 1,6      0       0	0 1	" 0 0 0 0 0 1 0 0 0 "
	0 0 0 УЭ 2,4     0      0      0      0	0	000100000
	0 0 0 УЭ34    0      0      0    УЭ3„ 3,4                                                  3,8	0	000100010
	0 0 0    0    УЭ 4,5     0      0      0	0	000010000
A =	0 0 0    0      0    УЭ 5,6     0      0	0 с> A =	000001000	. (1)
	0 0 0    0      0      0 УЭ 6,7     0	0	000000100
	0 0 0    0      0      0      0    УЭ 7,8	0	000000010
	0 0 0    0      0      0      0      0	УЭ 8,9	000000001
	. 0 0 0    0       0       0       0       0	0	. 0 0000000 0 .

Пусть испытуемому дано тестовое задание (ТЗ), состоящее из девяти вопросов закрытого типа [8]. Каждый вопрос ТЗ построен по СГ и ориентирован на выявление знания определенного УЭ. Результаты тестирования можно представить в виде матрицы ответов В на каждое ТЗ (пример — зависимость (2))

"0 0 0 0 0 0 0 0 0" 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 B = 0 0 0 0 0 1 0 0 0 (2) 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 .0 0 0 0 0 0 0 0 0. состоящей из единиц и нулей. Единице соответст- вует правильный ответ на вопрос ТЗ, нулю — не- правильный. Методики разработки ТЗ и обработки результатов тестирования подробно изложены в [9] и [10], а известные модели тестирования — в [11].

По матрице ответов испытуемого можно построить СГ (рис. 3), который будет соответствовать объему его знаний по предмету. По нему также будет видно, какие УЭ и какие связи между УЭ утрачены испытуемым.

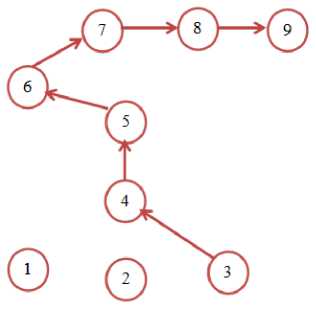
Рис. 3. Граф по результатам тестирования

Получим разность С между матрицами А и В :

	" 0	0	0	0	0	1	0	0	0 "
	0	0	0	1	0	0	0	0	0
	0	0	0	0	0	0	0	1	0
	0	0	0	0	0	0	0	0	0
C = 1 All -1BII =	0	0	0	0	0	0	0	0	0	. (3)
	0	0	0	0	0	0	0	0	0
	0	0	0	0	0	0	0	0	0
	0	0	0	0	0	0	0	0	0
	. 0	0	0	0	0	0	0	0	0 .

Матрицу А (см. зависимость (1)), построенную по эталонному графу (рис. 2), можно рассматривать как эталонную; матрицу ответов испытуемого на каждое ТЗ — В (см. зависимость (2)) — рассмотрим как фактическую матрицу знаний. По матрице С (см. зависимость (3)), являющейся разностью матриц (1) и (2), можно построить СГ, характеризующий индивидуальную траекторию требуемого обучения (рис. 4). Данный граф будет учитывать только те УЭ и только те связи между УЭ, которые конкретный испытуемый по результатам тестирования не усвоил (или утратил в своих знаниях). Таким образом, можно индивидуализировать процесс обучения на стадии теоретической подготовки и организовать процесс восстановления знаний после тестового контроля. Под восстановлением знаний понимается процедура, при которой по результатам деятельности обучаемого можно не только определить, какие знания недостаточны

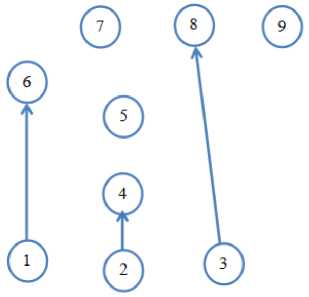
Рис 4. Граф, соответствующий индивидуальной траектории обучения или ошибочны, но и вернуть его на соответствующий раздел теории или практики либо дать дополнительные разъяснения.

ВУЗУАЛИЗАЦИЯ И КОНТРОЛЬНОЕ МОДЕЛИРОВАНИЕ СЕМАНТИЧЕСКИХ ГРАФОВ

Для визуализации и контрольного моделирования разработанного СГ целесообразно использовать язык программирования JavaScript совместно с библиотекой визуализации Arbor.js. Данный подход не только позволяет относительно просто создавать функции отрисовки каждой вершины и грани графа, но и обеспечивает создаваемому приложению корректную работу в глобальной сети Интернет, что немаловажно при реализации

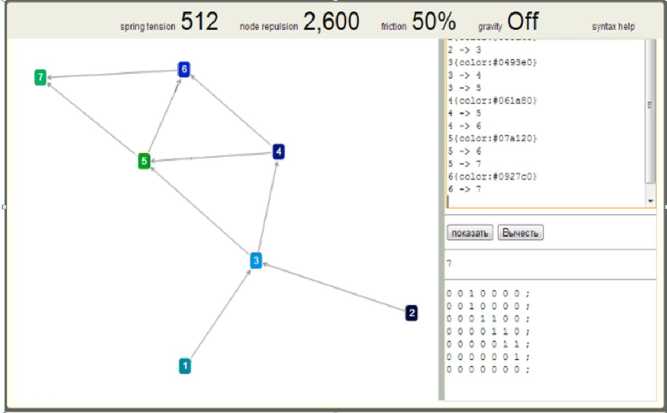
Рис. 5. Конструирование и контрольное моделирование семантического графа

дистанционного и адаптивного процесса обучения. На рис. 5 представлено окно программы, позволяющей в реальном масштабе времени конструировать и моделировать СГ любого вида и размерности, а также производить над моделями простейшие арифметические операции.

Конструирование графа осуществляется в следующем порядке. C персонального компьютера (ПК) производится запуск исполняемого файла программы, при этом автоматически осуществляется загрузка интернет-браузера (по умолчанию, Internet Explorer).

В появившемся диалоговом окне программы необходимо задать число вершин ( n ) графа. Подтверждаем свой выбор нажатием левой клавиши манипулятора типа "мышь"; на рабочем поле программы должна сформироваться единичная матрица связи размерностью n×n . (см. рис. 5). Далее в сформированной матрице с клавиатуры следует задать следующие виды связи: 1 — вершины графа связаны между собой, 0 — связь между вершинами отсутствует. Нажать левой клавишей манипулятора типа "мышь" на кнопку "показать". Главное поле программы заполнится информацией о связи узлов графа. Для визуализации графо– семантической модели необходимо с помощью клавиатуры нажать на кнопку "Enter". В результате описанного действия на экране ПК появится диалоговое окно программы в соответствии с рис. 5. Разработанная программа также позволяет строить графовые модели в автоматическом режиме.

Наиболее прогрессивными в настоящее время являются адаптивные модели тестирования [12]. Основным критерием для адаптации является сложность ТЗ, для определения которой также может быть использован рассмотренный ранее СГ [1].

В данном СГ (см. рис. 3) различают входные, внутренние и выходные концепты. Входные концепты — это понятия или же определения раздела знаний (δ — направление ветра, γ — курс полета, λ — угол сноса и т. д.), внутренние концепты используются для определения других понятий раздела, являются следующим уровнем графа (β — путевой угол, ε — угол ветра и т. д.), и выходные концепты — понятия, не использующиеся для определения других понятий курса (ψ — курсовой угол). Очевидно, что концепт, связанный с большим количеством других концептов, позиционируется как более сложный. В данном конкретном случае вопросы, ориентированные на знания входных концептов (1-й уровень), считаются наиболее простыми. Это, как правило, фундаментальные определения и понятия курса "Воздушная навигация". Данным вопросам присваивается наи- меньший вес. Вопросы, ориентированные на знания концептов высших уровней — 2, 3, 4 — соответственно считаются более сложными и, как следствие, имеют больший вес. Таким образом, нетрудно моделировать задания различного уровня сложности.

Адаптивное тестирование (АТ) предполагает, что выбор следующего задания зависит от ответа испытуемого на предыдущий вопрос. Анализ ответов проводится электронным инструктором. Функции электронного инструктора могут быть реализованы на основе использования аппарата "жесткой логики", аппарата "размытых" (нечетких) множеств [13] с использованием искусственных нейронных сетей (ИНС) [14, 15]. При использовании нечеткой логики появляется возможность оценить степень приближения ответа обучаемого к эталону [16], использовать нечеткую 12-балльную шкалу оценивания [17], что немаловажно при реализации в качестве сценариев обучения ТЗ открытого типа [11] и адаптивных тестовых заданий (АТЗ). Аппарат ИНС может быть применен как эффективное средство автоматизации диагностики знаний обучаемого.

ПРИМЕР КОМБИНИРОВАННОГО НЕЙРОГРАФОСЕМАНТИЧЕСКОГО ПОДХОДА

Рассмотрим в качестве примера решение с использованием аппарата ИНС задачи о "разрезании" эталонного СГ (рис. 2) и построении индивидуальной траектории обучения. Ранее было показано, что индивидуальную траекторию обучения можно определить в виде отдельных, связанных между собой ребрами, элементов эталонного СГ (рис. 2). Представим эталонный СГ в виде сети (рис. 6), в которой каждому конкретному УЭ будет соответствовать искусственный нейрон, ребра СГ являются входными и выходными связями нейрона. На рис. 6 представлена слабосвязная однослойная ИНС прямого распространения на базе персептронного нейрона (ПН) [18].

Математическая модель ПН описывается соотношениями (4) и (5).

Текущее состояние нейрона будет иметь вид

• ⁵ = & • wi ,             (4)

I = 1

где w i — вес синапса, i = 1... n ; x i — компонент входного вектора (входной сигнал), n — число входов нейрона, s — результирующая функция. В качестве результирующей функции может быть использована любая арифметическая или логическая операция (обычно используется взвешенная сумма).

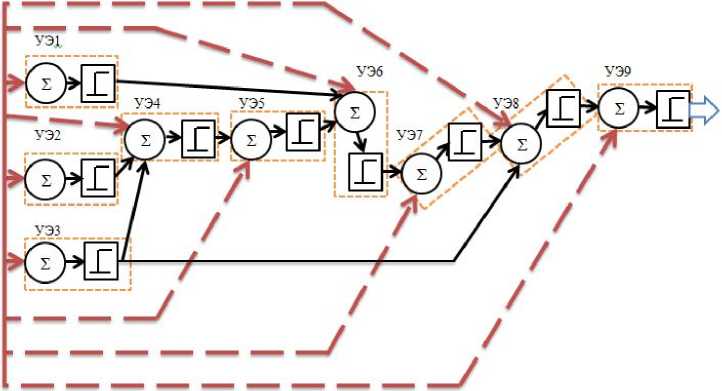
Рис. 6 . Семантический граф на базе нейросети

Выход ПН есть функция его состояния y = f (s),                       (5)

где y — выходной сигнал нейрона; f — пороговая функция активации, описываемая соотношением (6):

• 1,    s ^ t ;

У = f ( s ) = ln                    (6)

[0, s < T, где Т — некоторое пороговое значение.

Очевидно, что ПН полностью описывается своими весами w i и активационной функцией f ( s ). Получив набор чисел (вектор или матрицу) x в качестве входов, нейрон выдает 0 или 1 на выходе.

Так как процесс функционирования ИНС, т. е. сущность действий, которые она способна выполнять, зависит от весов синаптических связей, то, задавшись определенной структурой (топологией, архитектурой) ИНС, отвечающей какой-либо задаче, разработчик должен найти оптимальные значения всех переменных весовых коэффициентов. Этот этап называется обучением сети, и от того, насколько качественно он будет выполнен, зависит способность сети решать поставленные перед ней задачи во время функционирования [15].

ПРОЦЕСС ОБУЧЕНИЯ ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ

Алгоритм обучения — это набор формул, который позволяет по вектору ошибки вычислить требуемые поправки для весов сети. Оказывается, что после многократного предъявления примеров веса сети стабилизируются, причем сеть дает правиль- ные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что "сеть выучила все примеры", "сеть обучена" или "сеть натренирована". В программных реализациях можно видеть, что в процессе обучения функция ошибки (например, сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда функция ошибки достигает нуля или приемлемого малого уровня, тренировку останавливают (рис. 7).

Алгоритм обучения однослойной персептронной сети подробно описан в [14, 15, 19]. После завершения процесса обучения полученную сеть считают натренированной и готовой к применению.

Контроль, диагностика и восстановление знаний посредством графосемантического и нейросетевого подходов осуществляется следующим образом: обучаемому предлагается ТЗ закрытого типа [8], каждый вопрос которого связан с определенным УЭ эталонного СГ (рис. 2). По результатам тестового контроля ответы обучаемого представляются в виде фактической матрицы, состоящей из бинарных элементов. Бинарной единице соответствует правильный ответ обучаемого, бинарному нулю — неправильный.

Фактическая матрица (2), составленная из ответов обучаемого на тест, подается на вход обученной ИНС. Сеть осуществляет автоматизированный контроль знаний, выставляя оценку за ТЗ в соответствии со шкалой оценивания [17] (обычно используется классическая 4-балльная шкала). Диагностика знаний нейросетью осуществляется за счет возможности получать матрицу связности (МС) сети [15]. МС получается в результате обучения сети и характеризует связь и передачу сиг- налов от нейрона к нейрону; по МС можно судить о том, какие нейроны в сети были в состоянии возбуждения. Все выходы ПН принимают значения 0 и 1, единице соответствует возбужденное состояние (осуществляется передача сигнала), нулю — состояние покоя (сигнала нет). Так как каждый ПН сети соотнесен с УЭ из эталонного СГ (рис. 2), и на каждый УЭ задается вопрос из ТЗ, то по состоянию того или иного нейрона в МС можно установить, на какой вопрос обучаемый не ответил, соотнести этот вопрос с номером УЭ, на знание которого он был задан, дать дополнительные разъяснения, связав УЭ с ПрО, и отослать обучаемого к соответствующему разделу теории. По разности эталонной матрицы (1) и МС сети, можно построить матрицу, реализующую СГ, которая представляет собой индивидуальную траекторию обучения предметной области, что позволяет реализовывать адаптивное обучение.

Таким образом, очевидно, что совместное использование графосемантического и нейросетевого подходов позволяет осуществлять адаптацию и индивидуализацию освоения и усвоения УМ изучаемой дисциплины [7], реализовывать различные сценарии обучения (ТЗ закрытого типа, АТ), использовать широкую номенклатуру шкал оценивания (как классических, так и нечетких) [16]. С помощью данного гибридного подхода появляется возможность осуществлять не только контроль, но и диагностику с последующим восстановлением знаний.