Опыт применения программных средств TriadNS для моделирования социальных сетей

В настоящее время виртуальные социальные сети находят все более широкое распространение. Виртуальная социальная сеть – это специальный интернет-ресурс, позволяющий ее участникам, вне зависимости от их текущего местоположения, общаться со своими родственниками, коллегами и друзьями, обмениваться с ними различной информацией, а также искать интересующие данные. На сегодняшний день насчитывается более миллиарда пользователей социальных сетей. И если ранее социальные сети использовались в основном для общения между людьми, то в настоящее время они используются различными компаниями для решения рабочих вопросов, для работы с клиентами, для поиска

Работа выполнена при финансовой поддержке гранта РФФИ 13-07-96506 № р-юг-а.

информации, для распространения рекламы. Структура виртуальных социальных сетей сходна со структурой социальных сетей в реальном мире. Таким образом, изучение социальных сетей позволяет изучить принципы распространения информации, организации групп пользователей, способы привлечения клиентов.

Авторы работы [1] выделяют два основных подхода к анализу социальных сетей: статический и динамический.

Первый подход подразумевает изучение структуры сети (топологии), ее основных свойств (смежность, степень центральности, расстояние и др.). В рамках данного подхода делается "снимок" социальной сети и анализируется ее текущее состояние. Основное внимание уделяется геометрической форме сети, а также различным связям между вершинами (участниками социальной сети). Статический (структурный) подход позволяет достаточно точно характеризовать текущее состояние системы, однако не позволяет увидеть многие закономерности, которые становятся заметны только при изучении развития структуры сети.

Рассмотрение социальной сети в динамике позволяет проследить различные этапы ее формирования, выделить основные закономерности образования связей между вершинами и ход образования кластеров в графе.

В настоящее время существует большое количество специализированных программных систем, которые предназначены для изучения социальных сетей.

Рассмотрим возможность применения симулятора компьютерных сетей TriadNS[2] для исследования социальных сетей.

К программным средствам симуляторов социальных сетей можно предъявить следующие требования:

• -    Симулятор должен располагать программными средствами построения ин-тернет-графов. При построении интернет-графов необходимо соблюдать соответствие свойств генерируемого графа свойствам реальных социальных сетей. [5]. Так, показатели распределения степеней вершин генерируемого моделью графа должны быть близки к экспериментальным. Например, показатели распределения степеней вершин многих социальных сетей меньше 2. Еще одним критерием является гибкость программных средств, которые позволяют оперативно менять параметры моделей интернет-графов.

• -    Симулятор должен располагать программными средствами исследования ин-тернет-графов.

• -    Симулятор должен уметь имитировать поведение пользователей.

• -    Симулятор должен уметь работать с большими объемами данных, т.е. должен обладать программными средствами, позволяющими использовать вычислительные мощности нескольких вычислительных узлов или процессоров.

Рассмотрим, какими свойствами из перечисленных выше обладает симулятор компьютерных сетей TriadNS, а именно, укажем на особенности представления имитационной модели.

Представление имитационной модели в TRIADNS

Симулятор компьютерных TriadNS был разработан на основе системы автоматизированного проектирования и моделирования Triad [3, 4], которая была спроектирована и реализована сотрудниками кафедры математического обеспечения вычислительных систем ПГНИУ в 80-е годы прошлого века. Система Triad предназначалась для проектирования и моделирования вычислительных систем. В 2002 г. работы были возобновлены (Triad.Net, язык разработки С#) и продолжаются по сей день.

В TriadNS принято трехуровневое представление имитационной модели: M = (STR, ROUT, MES), где STR – слой структур, ROUT – слой рутин, MES – слой сообщений.

Слой структур представляет собой совокупность объектов, взаимодействующих друг с другом посредством посылки сообщений. Каждый объект имеет полюсы (входные и выходные), которые служат соответственно для приёма и передачи сообщений. Основа представления слоя структур – графы. В качестве вершин графа следует рассматривать отдельные объекты (например, концентраторы, маршрутизаторы, серверы, рабочие станции). Дуги графа определяют связи между объектами.

Имитационная модель имеет иерархическое представление. Отдельные объекты, представляющие вершины графа, могут быть расшифрованы подграфом более низкого уровня и т.д.

Объекты действуют по определённому сценарию, который описывают с помощью рутины. Рутина представляет собой последовательность событий ei, планирующих друг друга (E – множество событий; множество событий рутины является частично упорядоченным в модельном времени). Выполнение события сопровождается изменением состояния объекта. Состояние объекта определяется значениями переменных рутины. Таким образом, система имитации является событийноориентированной.

Рутина так же, как и объект, имеет входные и выходные полюса. Входные полюса служат соответственно для приёма сообщений, выходные полюса – для их передачи. В множестве событий рутины выделено входное событие ein. Все сообщения, которые поступают на входные полюса рутины, обрабатываются входным событием. Обработка сообще- ний, которые генерируются на выходных полюсах рутины, осуществляется обычными событиями рутины. Для передачи сообщения служит специальный оператор out (out through <имя полюса>). Совокупность рутин определяет слой рутин ROUT.

Слой сообщений (MES) предназначен для описания сообщений сложной структуры.

Система моделирования Triad реализована таким образом, что пользователю необязательно описывать все слои. Так, если возникает необходимость в исследовании структурных особенностей модели, то можно описать только слой структур.

Triad-модель рассматривается как переменная. Она может быть построена с помощью операций над моделью.

Как уже было сказано ранее, модель включает описание структуры, рутин и слоя сообщений.

Рассмотрим синтаксис слоя структур:

structure <имя структуры> def (<список настроечных параметров>) (<список входных и выходных параметров>) <описание переменных><операторы>) endstr

В качестве переменных можно использовать переменные типа "вершина", "граф", "полюс" и т.д. Операторы выполняют операции над вершинами, графами, полюсами, структурами.

Ниже приведен пример описания структуры компьютерной сети, состоящей из сервера и нескольких клиентов (в слое структур).

structure КлиентСервер[integer чис-лоКлиентов ] def КлиентСервер := node Сервер<ПРИЕМ,ВЫДАЧА> + node Клиент[0:числоКлиентов-1]

<ПРИЕМ,ВЫДАЧА>;

integer i;

for i := 0 by 1 to числоКлиентов - 1 do КлиентСервер := КлиентСервер + arc( Клиент[ i ].ВЫДАЧА -- Сер-вер.ПРИЕМ ) +arc(Сервер.ВЫДАЧА--Клиент[i ].ПРИЕМ );

endf;

endstr

Слой структур с описанием структуры компьютерной сети " Клиент-сервер "

Здесь представлена структура сети "КлиентСервер", которая строится в виде вершины "Сервер" и присоединенным к ней массивом вершин "Клиент".

Связи между вершинами устанавливаются в цикле for с помощью дуг, при этом указываются входные и выходные полюса (arc(Сервер.ВЫДАЧА—Клиент[i].ПРИЕМ )).

Слой структур представляет собой параметризованную процедуру. Изменив значение входного параметра "числоКлиентов", можно получить в результате модель со структурой, в которой определено уже другое количество клиентов.

Переопределить количество клиентов можно перед началом или в ходе имитационного эксперимента. Во втором случае переопределение выполняется в условии моделирования.

Сценарий работы клиента описывают с помощью рутины, синтаксис и текст которой приведены ниже:

Синтаксис:

routine<имя>(<список настроечных параметров>)(<список входных и выходных формальныхх параметров>) initial <последовательность операторов> endi event <последовательность операторов> ende event <наименование события><последовательность операторов> ende … event<наименование          собы- тия><последовательность операторов> ende endrout

Пример рутины:

routine Клиент ( input ПРИЕМ; output ВЫДАЧА )[ real deltaT ]

initial boolean запросПослан;

запросПослан := false ;

schedule ЗАПРОС in 0;

Print "Инциализация клиента"; endi event ЗАПРОС;

out "Запрос на обслуживание" through ВЫДАЧА;

Print "Клиент послал запрос серверу";

schedule ЗАПРОС in deltaT;

ende endrout

Рутина " Клиент "

Рутина также представляет собой параметризованную процедуру, которая наряду с параметрами интерфейса (входные и выходные полюса рутины "Прием" и "Выдача"), включает формальные параметры deltaT – временной интервал между запросами Клиента к Серверу.

Экземпляры рутин формируются оператором let Клиент( clientDeltaT ) be клиент, а наложение рутины на соответствующую вершину графа выполняется оператором put клиент on Модель.Клиент[i]<ПРИЕМ=ПРИЕМ, ВЫДАЧА=ВЫДАЧА>.

При этом входные и выходные полюса рутины сопоставляются с входными и выходными полюсами вершины.

Итак, мы описали программные и языковые средства симулятора TriadNS. Теперь рассмотрим модели случайных графов и результаты их реализации в TriadNS.

Модели случайных графов

В настоящее время для построения различных моделей социальных сетей применяют теорию случайных графов. Существует много видов моделей, генерирующих случайные графы, близкие по свойствам к реальным сетям [5]. Их можно разделить на несколько основных классов:

• -    Модели случайных графов (модель Эрдёша–Реньи).

• -    Простейшие модели безмасштабных сетей (модель Боллобаша–Риордана, модель копирования и др.).

• -    Более гибкие модели безмасштабных сетей (модель Чунг-Лу, модель Янсо-на–Лучака).

• -    Модель стохастических графов Кронекера.

Рассмотрим более подробно некоторые из моделей интернет-графов. Первой обсуждаемой моделью является модель Эрдёша–Реньи.

Модель Эрдёша–Реньи на данный момент является самой изученной моделью случайных графов [6]. Но, в начале 2000-х гг., выяснилось, что она плохо подходит для описания графов, возникающих в реальных социальных

сетях.

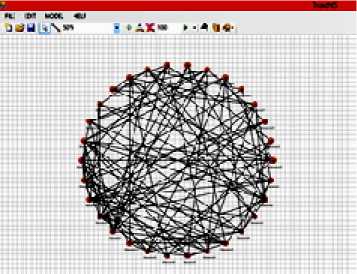
Рис. 1. Случайный граф модели Эр-дёша–Реньи с 30 вершинами и p=0,25

Итак, пусть дано множество

V n = {1, . . . , n}, элементы которого являются вершинами графа. Для построения случайного графа будем соединять вершины графа из множеств V n множеством соединяющих их ребер. Множество E является случайным. В данном случае не рассматриваются графы с кратными ребрами, графы с петлями и ориентированные графы (орграфы). Поэтому мы считаем, что потенциальных ребер у графа не больше, чем C_n ² штук. Будем соединять любые две вершины i и j ребром с некоторой вероятностью p ∈ [0, 1] независимо от всех остальных C_n ² - 1 пар вершин. Иными словами, ребра появляются в соответствии со стандартной схемой Бернулли, в которой C_n ² испытаний и "вероятность успеха" p. Обозначим через E случайное множество ребер, которое возникает в результате реализации такой схемы. Положим G = (V n , E). Это и есть случайный граф в модели Эрдёша–Реньи.

В настоящее время в симуляторе компьютерных сетей TriadNS возможно построение такого случайного графа. Для построения графа выбирают соответствующий пункт меню в графическом редакторе TriadNS, задают соответствующие параметры, а именно, количество вершин в графе и вероятность, с которой будет проведено ребро между любыми двумя вершинами и запускают соответствующую процедуру.

Пример модели Эрдёша–Реньи для случайного графа из 30 вершин c вероятностями 0,25 проведения ребер между любыми двумя вершинами приведен на рис. 1. При вероятности равной 1, получаем полный граф (рис. 2.).

Рис. 2 . Случайный граф модели Эрдёша–

Реньи с 30 вершинами и p=1

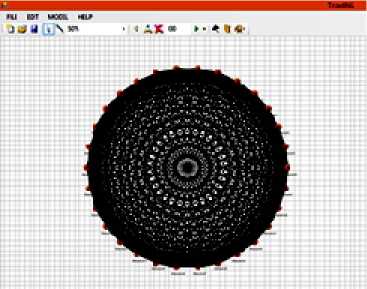
Полный граф (p=1) может быть построен с помощью графовой константы comple(n), где n – количество вершин. Используя графовые константы и операции над структурой: добавление вершин, добавление ребер, объединение и пересечение графов и т.д., – можно строить модели случайных графов.

Следующей обсуждаемой моделью является модель графа Барабаши–Альберта.

Введем прежде всего понятие интернет-графа [5] (или веб-графа). Интернет-граф -это граф, вершинами которого являются какие-либо конкретные структурные единицы в интернете: страницы, сайты, хосты.

Обычно принято считать вершинами веб-графа сайты, а ребрами соединять те вершины, между которыми есть ссылки. При этом число ребер между вершинами равно числу ссылок между соответствующими сайтами, возможны ссылки сайта на себя (т.е. петли), ребра разумно полагать направленными.

Таким образом, интернет-граф является ориентированным, он имеет кратные ребра и петли [6].

Интернет-графы обладают следующими свойствами:

• 1.    Интернет-графы формируют добавлением к нему новых вершин, соединяемых ребрами со старыми вершинами.

• 2.    Диаметр интернет-графа мал (примерно 5–7). Это свойство соответствует известному свойству любой социальной сети, поскольку известно, что "мир тесен".

• 3.    Интернет-граф имеет степенное распределение вершин. Этот факт роднит интернет со многими реальными сетями – социальными, биологическими и транспортными. Они также подчиняются степенному распределению, только имеют другой показатель распределения λ . Графы со степенным распределением степеней вершин называют без-масштабными . Исходя из своих наблюдений, Барабаши и Альберт ввели понятие предпочтительного присоединения [8].

Модель графа Барабаши–Альберта (граф БА) представляет собой алгоритм генерации случайных безмасштабных сетей с использованием правила предпочтительного связывания (ПС) [11].

Правило предпочтительного связывания гласит, что чем большую степень связности имеет вершина, тем выше вероятность присоединения к ней новых вершин. Если для присоединения выбирать вершину случайным образом, то вероятность выбора определенной вершины будет пропорциональна ее степени связности [9]. Правило соответствует принципу "богатый становится богаче". Данный граф выращивается из небольшого графа-"затравки", у которого степень связности каждой вершины должны быть не меньше единицы. Каждая новая вершина присоединяется к уже существующим вершинам с вероятностью пропорциональной степени связности этих вершин.

В качестве графа-затравки берется полный граф из трех вершин. Пользователь вводит количество вершин и количество ребер, которые будут прибавляться при создании новой вершины.

Каждая новая вершина соединяется с существующими вершинами с вероятностью, пропорциональной числу связей этих вершин [10].

Наиболее связанные узлы ("хабы"), как правило, накапливают еще больше связей, тогда как узлы с небольшим числом связей вряд ли будут выбраны для присоединения новых узлов. Новые узлы имеют "предпочтение" соединяться с наиболее связанными узлами.

Пример построения графа с 30 вершинами и добавлением трех вершин на каждом шаге приведен на рис. 3.

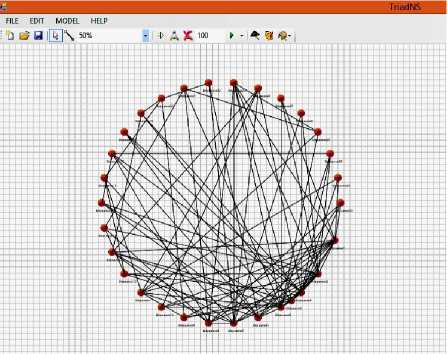
Рис. 3. Модель графа Барабаши–Альберта

Итак, в настоящее время разработаны процедуры для построения ряда моделей социальных сетей (класс случайных графов, класс безмасштабных сетей) [12]. Процедуры являются параметризованными.

Программные средства исследования графа

Социальные сети могут характеризоваться множеством разных метрик, ниже приведены некоторые из них:

• 1.    Взаимная направленность – свойство показывает, является ли отношение между вершинами бинарным (является ли связь двунаправленной).

• 2.    Гомогенность – указывает на степень появления связей между похожими акторами (по полу, возрасту, интересам) [11].

• 3.    Транзитивность связей – увеличение вероятности появления связей между акторами, у которых есть связи с одними и теми же вершинами [13].

• 4.    Разница в распределении – указывает на большое количество связей у одних акторов и минимальное у других. Важным в данном случае является феномен "богатый становится богаче", который приводит к высокой дисперсии вершин.

• 5.    Центральность – метрика, которая позволяет определить значительность или влияние определенного узла или группы в сети [14].

• 6.    Ассортативность – склонность к образованию связей между вершинами большой степени [15].

• 7.    Диаметр сети.

Для определения характеристик графа в TriadNS существует большое количество стандартных процедур.

На рис. 4. представлено окно, в котором следует указать те характеристики, которые интересуют пользователя.

4 Вычисление характеристик

Центральность

0 Степень центральносьтм й Центральность как посредничество

0 Плотность центральности

0 Собственный вектор центральности

Кратчайшее растояние

• 1= 1 Кратчайшее растояние между ^и всеми элементами

  Разное

  0 Степень вершин

  0 Сильно связные компоненты

  0 Коэффициент кластеризации

  0 Обшие характеристики

  0 Кратчайший путь

  | dient1 ^т[ [Setver! ^[

  
  

[ Выделить все | [ Снять выделение |

[ВыЧИ^^ [ Выйти |

Рис. 4. Окно " Вычисление характеристик графа "

Заключение

Таким образом, в работе представлены программные и языковые средства симулятора компьютерных сетей TriadNS, которые позволяют строить случайные и интернет-графы с целью исследования социальных сетей. Программные средства TriadNS позволяют получить характеристики интернет-графов. Наряду с возможностями исследований характеристик графа возможно динамическое исследование социальных сетей. Динамическое исследование социальных сетей в настоящей статье подробно не рассматривается. Однако представленные языковые и программные средства TriadNS указывают на то, что TriadNS может успешно применяться для этого (слой рутин, информационные процедуры для сбора статистики во время имитационного эксперимента).

Кроме того, TriadNS дает возможность выполнять распределенное (параллельное) моделирование [16]. К тому же исследование социальных сетей может быть связано с обработкой больших объемов данных.