Организация прямого двигательного управления при наклонах корпуса человека

В литературе, посвященной теории двигательного управления в живых системах, обсуждаются две точки зрения на его организацию: 1) теория равновесной точки (РТ), подразумевающая управление равновесным положением биомеханической системы, и 2) теория внутренних нейронных моделей (ВНМ), подразумевающая непосредственный контроль силами мышц.

В соответствии с теорией РТ [9], мышечные усилия, обеспечивающие выполнение движения, определяются двумя факторами: во-первых, изменением желаемой контролируемой центрально-равновесной конфигурацией тела (“ reference frame ”, [9]) и, во-вторых, механизмом автоматической («пассивной») генерации мышечных сил по обратной связи (ОС) в ответ на отклонение текущей (реально наблюдаемой) его конфигурации от желаемой равновесной. Таким образом, под прямым управлением (ПУ) в данной теории подразумевается управление изменением равновесной конфигурации тела и параметрами петли ОС, но не непосредственный контроль мышечных усилий или непосредственный контроль наблюдаемой

Александров Алексей Владимирович, к.б.н., с.н.с. Института высшей нервной деятельности и нейрофизиологии, Москва

Фролов Александр Алексеевич, д.б.н., к.ф.-м.н., профессор, заведующий лабораторией математической нейробиологии обучения, Москва кинематики. При этом петля ОС характеризуется достаточно большими коэффициентами усиления, чтобы обеспечить успешное (устойчивое) выполнение двигательной задачи.

В теории двигательного управления на основе ВНМ [16, 23], в отличие от теории РТ, механизм ОС существенной роли в управлении движением не играет. Предполагается, что в ВНМ «выучены» геометрические и инерционные характеристики тела. Нервная система «заранее» программирует желаемую кинематику движения и, с учетом ВНМ, рассчитывает необходимые для ее реализации мышечные силы путем решения обратной задачи динамики. Рассчитанные «запрограммированные» силы непосредственно генерируются исполнительным нейромышечным аппаратом для выполнения желаемого движения. Иными словами, если в теории РТ центральное ПУ связывается с управлением равновесным положением системы («статикой»), а силы генерируются автоматически по петле ОС, то в теории ВНМ под непосредственным ПУ находятся действующие в системе силы («динамика»), а значение механизмов ОС невелико. Считается, что некоторая коррекция мышечных сил по ОС происходит только при наличии неожиданных возмущений, приводящих к отличию наблюдаемой кинематики от желаемой. При этом коэффициенты усиления в петле ОС недостаточны, чтобы без прямого управления силами обеспечить близкое совпадение желаемой и наблюдаемой кинематики [13].

Справедливость одной из этих теорий двигательного управления при интерпретации экспериментальных данных определяется путем оценки коэффициентов усиления в петле ОС. Если они достаточно велики для успешного выполнения движения при относительно простой форме сигнала ПУ [14] без непосредственного управления силами мышц, то разумно предположить, что ПУ происходит «статически» согласно теории РТ, в противоположном случае – «динамически» согласно теории ВНМ.

Стандартной процедурой для определения параметров сигнала ПУ и петли ОС является неожиданное возмущение выполняемого целенаправленного движения [3, 7, 11]. Использование данной процедуры позволяет экспериментатору разделить эффекты команд ПУ и управления по ОС при организации моторного контроля. Так, характерное время коррекции сигнала ПУ со стороны центральной нервной системы (ЦНС) в ответ на возмущение велико (порядка 5–10 с в случае прямого стояния человека [15]) по сравнению со временем автоматической коррекции по ОС (1–2 с). Поэтому коррекция мышечных усилий в начальной фазе ответа на возмущение происходит по ОС, а сигнал ПУ остается в этой фазе таким же, как и при «невозмущенном» выполнении наклона корпуса. Полагая, как принято в большинстве работ [2, 6–8, 11, 19–21], что управление по ОС является линейным, сравнение возмущенного и невозмущенного движений в их начальной фазе позволяет исключить из динамического уравнения член, определяющий априори неизвестный временной ход сигнала ПУ. После такого исключения появляется возможность рассчитать параметры петли ОС, а, зная эти параметры и полагая в первом приближении, что они неизменны на протяжении всего двигательного акта, можно оценить и временной ход изменения сигнала ПУ и таким образом получить полное описание двигательного управления на биомеханическом уровне.

В предыдущей работе авторов [3] параметры петли ОС оценивались при выполнении наклона корпуса в сагиттальной плоскости у человека. Возмущение производилось путем неожиданного сдвига опорной платформы назад приблизительно на 8 см за 300 мс. В этой работе рассматривались три модели петли ОС. В первой модели (ОС1), как и в работах [2, 6–8, 11, 19, 20], петля ОС моделировалась в виде линейной вязкоэластичной пружины с временной задержкой. Коэффициент, определяющий изменение мышечных усилий в ответ на отклонение конфигурации тела от желаемой, называется жесткостью, а в ответ на отклонение скорости от желаемой – вязкостью. Во второй модели (ОС2), как и в работе [21], в петлю ОС дополнительно включался член, определяющий зависимость мышечных сил от отклонения ускорения от желаемого. В третьей модели (ОС3), как и в работе [21], предполагалось, что линейной пружинной модели удовлетворяют не сами мышечные силы, а активность мышц, оцениваемая по электромиограмме (ЭМГ). При этом преобразование активности мышц в силы определялось инерционным звеном первого порядка с постоянной времени 40 мс.

Параметры каждой из трех моделей петли ОС оценивались в [3] двумя различными методами, широко используемыми во многих исследованиях: с помощью решения либо прямой, либо обратной задачи динамики. При решении обратной задачи рассчитываются моменты мышечных сил по наблюдаемой кинематике и проводится линейный регрессионный анализ зависимости моментов сил от суставных углов, их скоростей и ускорений [1–3, 5–7, 11]. Полученные регрессионные коэффициенты и рассматриваются как искомые параметры петли ОС. При решении прямой задачи рассчитывается кинематика по заданным моментам сил. При этом силы задаются с помощью некоторой модели петли ОС, полученная кинематика сравнивается с наблюдаемой, и параметры петли ОС оптимизируются так, чтобы расчетная кинематика минимально отличалась от наблюдаемой [8, 17, 19, 21]. В этом случае в качестве искомых параметров петли ОС используются полученные оптимальные параметры.

В работе [3] было показано, что оба метода дают близкие значения параметров петли ОС, а дополнительный учет зависимости мышечных сил от ускорения и учет инерционного звена первого порядка для преобразования мышечной ЭМГ активности в мышечные силы практически не влияют на точность аппроксимации экспериментальных данных. Однако влияние вида рассматриваемых моделей ОС на оценку временного хода сигнала ПУ (хода изменения равновесной конфигурации тела) ранее не исследовалось. В настоящей работе данные, полученные в [3], используются для оценки этого временного хода.

С биомеханической точки зрения, управление движением и позой стоящего человека является достаточно сложной задачей. Последнее связано с тем, что тело человека представляет собой многозвенную биомеханическую цепь, так что движение в любом отдельно взятом суставе приводит к необходимости вырабатывать корректирующие силовые моменты во всех суставах. Сложность управления усугубляется тем, что наиболее массивный сегмент (корпус) расположен высоко над площадью опоры, размеры которой малы (ограничены длиной стоп). В предыдущих работах авторов [1, 4] было показано, что управление позой и движением у стоящего человека значительно упростилось бы, если в качестве независимых единиц двигательного управления ЦНС использовать движения вдоль собственных векторов динамического уравнения («естественные синергии»). В дальнейших работах [2, 3, 5, 6] было экспериментально подтверждено, что ЦНС действительно использует такую возможность и естественные синергии управляются независимо как напрямую, так и по обратной связи. При использовании трехсуставной модели тела (голеностопный, коленный и тазобедренный суставы) существуют три такие синергии. По доминирующему суставу их можно назвать А- (Ankle – голеностопный сустав), H- (Нip – тазобедренный сустав) и К- (Knee – коленный сустав) синергиями. Было показано, что поведенческие функции Н- и А-синергий существенно различаются. Непосредственно наклон обеспечивается Н-синергией, в то время как А-синергия является вспомогательной и служит для компенсации смещения центра тяжести CG (CG – Centre of Gravity), вызываемого этим наклоном. Именно это функциональное различие, по-видимому, обусловливает наблюдаемые изменения параметров петли ОС в случае выполнения целенаправленного наклона корпуса по сравнению со спокойным стоянием: в Н-синергии усиление в петле ОС возрастает, а в А-синергии снижается. В частности, жесткость в Н-синергии при выполнении наклона увеличивается приблизительно в полтора раза по сравнению с вертикальным стоянием. Увеличение жесткости в петле ОС типично при выполнении целенаправленных движений [11, 13, 14], поскольку именно такие движения непосредственно обеспечивают выполнение поведенческой задачи и поэтому должны контролироваться ЦНС «более жестко». В отличие от Н-синергии жесткость в А-синергии уменьшается до значения, нейтрализующего гравитационные силы, так что любая конечная конфигурация тела в А-синергии является нейтрально устойчивой. Тем самым любая конфигурация тела в А-синергии, достигаемая после завершения наклона, является допустимой для ЦНС, если она не приводит к выходу горизонтальной проекции CG за границы опоры, а значит и не приводит к потере равновесия. Функциональное различие Н- и А-синергий и различие в их управлении по ОС позволяет предположить, что в этих синергиях будет существенно различаться и характер изменения сигнала ПУ. Проверка данной гипотезы и является основной целью данного исследования.

Модель и методы

Протокол эксперимента

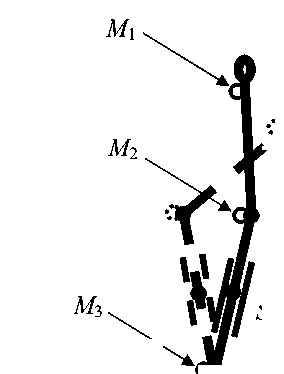
В экспериментах принимали участие пять здоровых испытуемых мужского пола в возрасте от 30 до 53 лет и весом от 73 до 99 кг. Максимально быстрый наклон корпуса вперед на приблизительно 40º из вертикального положения выполнялся в ответ на короткий звуковой сигнал. После завершения движения испытуемый сохранял наклонное положение в течение приблизительно 2 с. Коленные суставы испытуемого были блокированы с помощью специальных шин (рис. 1). Блокировка коленей производилась для упрощения анализа полученных данных, позволяя ограничиться двухзвенной биомеханической моделью тела испытуемого – корпус и нижние конечности, с вращением в двух цилиндрических суставах – голеностопном и тазобедренном.

M 3

S

>>>>>»»

Рис. 1. Расположение маркеров M1–M3 на теле испытуемого, совершающего быстрый наклон корпуса вперед в сагиттальной плоскости при блокированных с помощью специальных шин S коленях

Три светоотражательных маркера ставились на правую сторону тела: M 1 – плечо ( acromion ), M 2 – таз ( femoral trochanter ) и M 3 – стопа ( external malleolus ). Координаты маркеров регистрировались с помощью системы ELITE [10] с частотой опроса 100 Гц. Погрешность измерения координат маркеров составляла 0,78 мм. Угол наклона корпуса относительно вертикали определялся по линии, соединяющей маркеры М 1 – М 2 , а нижних конечностей – по линии М 2 – М 3 . Коленные суставы блокировались с помощью специальных шин, что позволяло ограничиться в настоящей работе рамками двухзвенной биомеханической модели.

Все данные для каждого испытуемого усреднялись по пробам, и процесс обработки проводился по усредненным данным с использованием стандартных методов статистического анализа (пакет программ SPSS ). Оценка вариабельности средних показателей по всем испытуемым приводится в виде «среднее±среднеквадратичное отклонение» ( Mean±SD ).

Представление движения в виде суперпозиции естественных синергий

Динамика движения тела человека в сагиттальной плоскости рассматривается в линейном приближении на основе модели двух твердых тел, вращающихся вокруг идеальных цилиндрических шарниров, моделирующих голеностопный и тазобедренный суставы. В работе [4] было показано, что для углов наклона корпуса Δ по отношению к вертикали, не превышающих 55º, среднюю ошибку вычисления суставных углов при решении прямой задачи динамики в линейном приближении по сравнению с точным решением можно оценить по формуле ε ≈ E Δ³, где коэффициент Е для испытуемого со «стандартными» антропометрическими параметрами (рост 1,7 м, масса 70 кг) составляет около 0,04 рад^–2 и относительная ошибка (ε / Δ) – менее 4%.

Экспериментальный протокол включал два типа движений: с возмущениями в виде неожиданного сдвига опоры во время выполнения наклона либо без возмущений на неподвижной опоре. Сравнение этих движений позволило вычислить параметры петли обратной связи у каждого из пяти испытуемых при выполнении ими наклона корпуса [3]. В настоящей работе полученные ранее значения этих параметров используются для расчета временного хода сигнала прямого управления. Для этого анализируются только записи движений на неподвижной опоре. В этом случае уравнение движения имеет вид

Сф - Dф = T , (1)

где φ – вектор углов в тазобедренном и голеностопном суставах, C и D – инерционная и гравитационная матрицы, T – вектор суставных моментов, создаваемых мышечными усилиями. В векторах φ и Т первая и вторая компоненты относятся соответственно к голеностопному и тазобедренному суставам.

Выражения для расчета элементов матриц C и D по антропометрическим параметрам приведены в работе [3]. Индивидуальные антропометрические параметры испытуемых рассчитывались с помощью стандартных таблиц [22] с учетом их веса, роста и длин звеньев тела.

Линейное приближение позволяет представить движение в виде суперпозиции двух составляющих («естественных синергий»), каждая из которых является движением вдоль одного из двух собственных векторов w i уравнения (1), определяемых уравнением

Cw , =l , Dw„ (2)

где λ i – собственные значения. Индексы i = H , А соответствуют доминированию тазобедренного ( H p ) или голеностопного ( Ankle ) суставов в каждом из собственных векторов [3].

Представление уравнения (1) в терминах естественных синергий предполагает преобразование вектора суставных углов φ ( t ) в вектор «кинематических амплитуд» ξ ( t ) путем обращения уравнения

φ ( t ) = W ξ ( t ),                                       (3)

где столбцы матрицы W – собственные векторы w i , а каждая из компонент вектора ξ ( t ) определяет временной ход движения вдоль соответствующего собственного вектора.

«Динамические амплитуды» η i для моментов мышечных сил в каждой из собственных синергий вычисляются путем подстановки (3) в (1). Принимая во внимание (2), получаем два независимых скалярных динамических уравнения для каждой из естественных синергий

-λiξi +ξi =ηi,(4)

где векторы динамических амплитуд η

η(t) = U-1T(t),(5)

а матрица

U = -DW определяет вклад каждой синергии в суммарные моменты сил в отдельных суставах. Как видно из (3) и (5), уникальным свойством движения вдоль собственного вектора уравнения (1) является линейная связь между изменениями суставных углов (кинематическая синергия) и одновременно линейная связь между изменениями суставных моментов (динамическая синергия). Именно поэтому эти два движения логично назвать естественными синергиями.

Каждое из уравнений (4) эквивалентно уравнению движения для перевернутого маятника с моментом инерции λ i . Взаимосвязь между перемещениями центра тяжести CG и центра давления CP , X i^CG и X i^CP , а также между соответствующими кинематическими и динамическими амплитудами, ξ i и η i , имеет вид

X i ^CG = b i ξ i ; X i ^CP = b i η i ,                                      (7)

где выражения для коэффициентов b i приведены в [3].

Метод оценки временного хода сигнала ПУ

Оценка временного хода сигнала ПУ зависит от принятой модели петли ОС. Как отмечалось выше, в настоящей работе рассматриваются три модели управления по ОС: ОС1 – модель вязко-эластичной пружины без учета ускорения, ОС2 – с учетом ускорения и ОС3 – с учетом ускорения и инерционного звена преобразования мышечной активности в мышечные силы. В модели ОС1 полагается, что корректирующие суставные моменты линейно зависят от суставных углов и угловых скоростей с временной задержкой. В терминах естественных синергий вместо корректирующих суставных моментов рассматриваются динамические амплитуды η , а вместо суставных углов рассматриваются кинематические амплитуды ξ . В работе [3] было показано, что естественные синергии при выполнении целенаправленного наклона корпуса независимо управляются по ОС, как это было ранее показано в случае поддержания вертикального стояния [2, 6]. Тогда корректирующая динамическая амплитуда η i в каждой из синергий полностью определяется кинематической амплитудой ξ i только в данной синергии, т.е. при независимом управлении в каждой из синергий петля ОС1 описывается следующим уравнением:

n ( t ) =i 0 ( t ) + K S i , ( t -T i ) + K V U t -T , ), i = Н , А ,                 (8)

где K i^S и K i^V – коэффициенты жесткости и вязкости в терминах естественных синергий, T i - временная задержка управления по ОС. Величина i ,⁰ является параметром, находящимся под прямым управлением ЦНС и определяющим текущую равновесную конфигурацию тела. При спокойном стоянии сигнал прямого управления i , ⁰ не изменяется и определяет желаемую равновесную конфигурацию при неподвижной позе i eq ( eq - equilibrium , равновесный). Из (4) и (8) следует, что при неподвижном стоянии и при K i^S ≠ 1

i eq = i i ⁰ /( K S - 1).                                  (9)

При выполнении наклона полное изменение сигнала i , ⁰ определяет амплитуду движения. Как было показано в [3], коэффициент жесткости K А^S для А -синергии во время выполнения наклона близок к единице: K А^S = 0,95±0,02, поэтому уравнение (9) для А -синергии неприменимо, и конечная равновесная конфигурация тела для этой синергии не определена: любая конфигурация, не приводящая к выходу горизонтальной проекции CG за границы опоры, является приемлемой, поскольку не приводит к потере равновесия. Напротив, для Н -синергии коэффициент жесткости K Н^S во время выполнения наклона отличался от единицы и составил около 1,7 ( K Н^S = 1,73±0,30), поэтому уравнение (9), однозначно определяющее конечную конфигурацию тела после выполнения наклона, справедливо только для H -синергии.

Для модели ОС2 уравнение (8) принимает вид

П , ( t ) =i 0 ( t ) + K? i , ( t -T , ) + K ,V i ,( t -T,) + K" i , ( t -T , ), i = Н , А ,          (10)

где последний член задает корректирующую поправку к мышечным силам с учетом ускорения.

Для модели ОС3 уравнение (10) принимает вид:

ЦП , ( t ) + n ( t ) =i° ( t ) + K ,^s i , ( t -T , ) + K V i , .( t -T , ) + K ia i , .( t -T , ), i = Н , А , (11) где µ – постоянная времени инерционного звена преобразования активности мышц в силы, которая, следуя [21], принималась равной 40 мс. Нужно заметить, что наличие инерционного звена с постоянной времени ц в уравнении (11) эквивалентно, в некотором приближении, запаздыванию на величину ц всего сигнала в правой части дифференциального уравнения (10).

Очевидно, что для моделей ОС2 (10) и ОС3 (11) в случае спокойного стояния равновесная конфигурация тела для Н -синергии Ь Н^еч определяется тем же уравнением (9).

Комбинируя динамическое уравнение (4) с одним из уравнений (8), (10) или (11), получим уравнение для оценки временного хода сигнала прямого управления i , ⁰( t ) в зависимости от выбранной модели ОС. Для модели ОС1

ii0 (t) = -^iii(t) + ii(t)-K ii(t-Ti)-KVii(t-Ti), i =

Н , А ,           (12)

T , ), , = Н , А ,     (13)

для модели ОС2

i,0 (t }=-x, i, (t)+i( t) - K? i, (t-T,) - K*' i f( t-t,) - K-i X t - а для модели ОС3

i,(t)=ц [_^,4-(t)+i,(t) ]- ^^i(t)+i,(t)-- KS i, (t-t, ) - kv i ;(t-t, ) - Ka ^; xt-t,), ,=н , а

При Ki > 1, т.е. в случае Н-синергии, полученная величина Ёi0(t) может быть представлена в виде у (t)=Eeq (t) - к? ёчt), что соответствует представлению, например, модели ОС1 в виде n, (t )=v (t) + K? [ЁЛ t-Ti) S'" (t)] + к-Ё,(t-t,), где первое слагаемое соответствует мышечным усилиям, направленным на преодоление статических сил гравитации, а второе и третье слагаемые – на преодоление инерционных сил. При этом Ёeq(t) определяет текущую равновесную конфигурацию тела в том смысле, что если в любой момент времени t0 зафиксировать Ёeq(t) = Eieq(10) = const, то конфигурация тела Ei(t) будет стремиться к конфигурации Ёie(t0) как к равновесной стационарной конфигурации. В частности, если Eiie(t) изменяется достаточно медленно, то конфигурация Ei(t) будет всегда близка к Ёeq(t). Такая интерпретация сигнала ПУ Ei0(t) соответствует теории РТ [9].

Другая интерпретация сигнала Ё 0 ( t ), которая согласуется с теорией ВНМ с помощью решения обратной задачи динамики [16, 23] (т.е. с «динамической моделью» ПУ), соответствует представлению модели ОС1 в виде

n ( t ) =n com ( t ) + K^S [ E ( t -t ) -E des ( t - 1 )] + K^- [ E ( t - t ) -E des ( t -t )],         (15)

где E des ( t ) — желаемый ( des - desired ) временной ход движения, а П com ( t ) = -ХЁ ^des ( t ) + E ^des ( t ) - временной ход команды ПУ мышечными силами, обеспечивающими желаемое движение. Требуемые силы генерируются ЦНС на основе решения обратной задачи динамики с помощью ВНМ, входом в которую является E ^des . В случае, когда реальное движение совпадает с желаемым ( E = E ^des ), второе и третье слагаемые в (15) равны нулю и мышечные силы полностью определяются центральной командой n com . Коррекция мышечных сил, рассчитанных с помощью ВНМ, производится только в случае, когда реальное движение отличается от желаемого, например, вследствие внешних возмущений. В рамках данной теории сигнал прямого управления E ⁰( t ), в соответствии с (15), представляется в виде

E ⁰ ( t ) =n com - k^s e ^des ( t - t ) - к^- E ^des ( t -t ) .                        (16)

Если принять, что ВНМ уже «обучена» так, что без внешних возмущений реальное движение совпадает с желаемым ( Ё = Ё des ), то уравнение (16) совпадает с (12).

Очевидно, что по экспериментальным данным, позволяющим только оценить по формулам (12)-(14) временной ход Ё 0 ( t ), в принципе невозможно отдать предпочтение организации ПУ в соответствии с теорией РТ или с теорией управления по ВНМ. В пользу первой теории говорит ее простота, так как в этом случае ЦНС требуется обучиться генерировать только статический управляющий сигнал E ^eq , определяющий статическую равновесную конфигурацию тела. При этом переход из одного статического состояния в другое происходит за счет простого изменения E ^eq от начального до конечного значения (например, с постоянной скоростью [9]). В пользу второй теории говорит ее универсальность, так как она объясняет способность ЦНС организовать движение со сколь угодно сложным характером изменения его траектории и скорости. Однако это достижимо за счет более сложного процесса формирования ВНМ для решения обратной задачи динамики . Таким образом, решающим аргументом в пользу выбора первой или второй теории для объяснения экспериментальных данных служит простота или сложность полученного управляющего сигнала E ⁰( t ). В настоящей работе его простота оценивается точностью его приближения при линейной зависимости от времени.

Результаты

Сигнал прямого управления в Н-синергии

Параметры петли ОС, необходимые для расчета сигнала прямого управления ξ H ⁰ по уравнениям (12)–(14) для каждого из пяти испытуемых, рассчитывались индивидуально. Использованные параметры были получены тремя разными способами: 1) с помощью решения обратной задачи динамики; 2) с помощью решения прямой задачи динамики с минимизацией ошибки для скорости перемещения CG или 3) с минимизацией ошибки для положения CG . Их значения, усредненные по всем испытуемым, приведены в работе [3]. Временной ход сигнала ПУ для каждого испытуемого рассчитывался по данным, осредненным по всем его движениям на неподвижной опоре. Каждый из испытуемых совершал по 5–7 таких движений, чередующихся в случайном порядке с движениями на неожиданно смещаемой платформе.

На рис. 2, а жирной сплошной линией представлена типичная зависимость ξ Н ⁰( t ) сигнала ПУ от времени, рассчитанная для одного из испытуемых методом решения обратной задачи динамики по модели ОС1. Данная модель обратной связи является наиболее простой по сравнению с моделями ОС2 и ОС3. Для наглядности, в соответствии с уравнениями (7) и (9), сигнал ПУ представлен на графике в терминах равновесного положения CG : CG H^eq = b H ξ H ⁰/( K H^S – 1). Результаты, полученные для других испытуемых и других использованных моделей и методов, качественно сходны с представленными на рис. 2, а .

Штриховой и пунктирной линиями представлены соответственно перемещения CG Н и CР H по Н -синергии в зависимости от времени. Видно, что при выполнении наклона корпуса вперед CG по данной синергии смещается назад, так как в этом движении отклонение ног назад преобладает над отклонением корпуса вперед. В каждом из двух равновесных положений тела (начальном вертикальном и конечном наклонном) значения координат CG Н , CР H и CG H^eq , естественно, совпадают. В первой фазе выполнения наклона СР перемещается вперед, разгоняя СG назад, затем СР перемещается назад, обгоняя и тем самым тормозя СG . В отличие от перемещения СР , сигнал прямого управления CG H^eq меняется монотонно. Движение инициируется перемещением равновесного положения CG H^eq назад. Это приводит к отклонению текущего положения CG H от равновесного. В результате рассогласования текущего и равновесного положений CG возникают силы, увлекающие CG H вслед за CG H^eq . Для большинства моделей ОС и методов расчета параметров петли ОС, использованных в [3], перемещение CG H^eq заканчивается раньше, чем перемещение CG H , что согласуется с данными по исследованию движения руки [9]. В этом случае при приближении текущей конфигурации тела к конечной равновесной конфигурации «упругие силы ОС» исчезают и остановка движения происходит за счет «вязких сил ОС».

Тонкой сплошной линией на рис. 2, а показана аппроксимация CG H^eq функцией CG H^lin , линейно изменяющейся по времени от начального до конечного значения CG H^eq . Именно такой временной ход изменения равновесной конфигурации тела постулируется в теории РТ [9]. При построении CG H^lin подбирались моменты времени начала линейного отрезка t 1 и его конца t 2 (см. рис. 2, а ), обеспечивающие минимальную среднеквадратичную ошибку приближения. Как видно на рис. 2, а , такая линейная аппроксимация хорошо описывает характер изменения CG H^eq . Ошибки аппроксимации в процентах к размаху перемещения CG H^eq для всех моделей ОС и методов расчета параметров ОС приведены на рис. 3 (панель 4). В среднем по всем испытуемым, моделям и методам ошибка аппроксимации составила 5,2±3,1%.

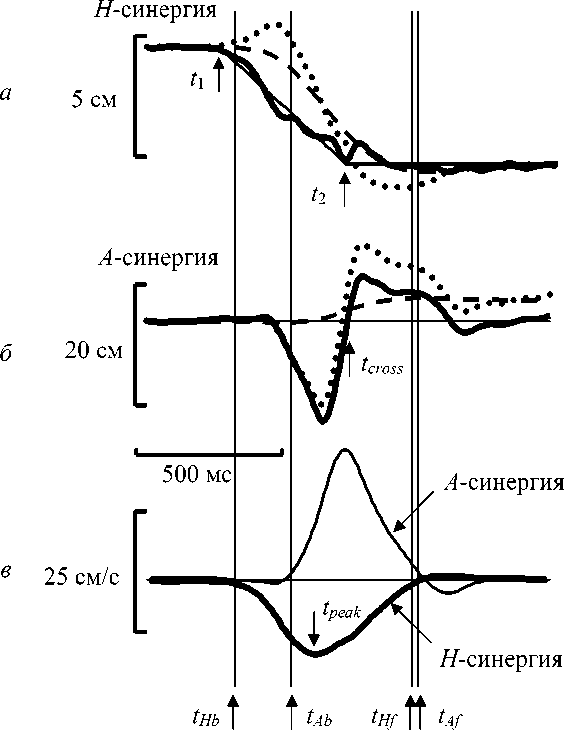
Рис. 2. Зависимость от времени перемещений по Н -синергии, панель ( а ), и по А -синергии, панель ( б ), для центра тяжести CG (штриховые линии) и центра давления CP (пунктирные линии). На панели ( а ) представлены также изменение равновесного положения центра тяжести для Н -синергии ( CG H^eq , жирная сплошная линия) и аппроксимация CG_H ^eq функцией CG_H ^lin (тонкая сплошная линия), которая начинает изменяться в момент t ₁ и прекращает – в момент t ₂. На панели ( б ) жирной сплошной линией представлен сигнал ПУ для А -синергии. Результаты показаны в среднем по пробам с наклонами на неподвижной опоре для одного из испытуемых. Приведенные временные зависимости для сигналов ПУ были рассчитаны методом решения обратной задачи динамики по модели ОС1. На панели ( в ) показаны профили скоростей перемещения центра тяжести по Н -синергии (жирная линия) и по А -синергии (тонкая линия). Вертикальные линии показывают моменты начала t Hb , t Ab и окончания t Hf , t Af движения в каждой из синергий, рассчитанные по пятипроцентному порогу от соответствующей максимальной скорости. Момент достижения пика скорости CG H отмечен вертикальной стрелкой t peak

Моменты начала t Hb и окончания t Hf движения по Н -синергии, рассчитанные по пятипроцентному порогу от максимальной скорости перемещения CG H , показаны на рис. 2 соответствующими вертикальными линиями. Момент достижения пика скорости CG H обозначен на рис. 2, в как t peak .

На рис. 3 представлены три временных параметра для зависимостей, приведенных на рис. 2, а , в : разность ∆ t b = t Hb – t 1 между временами начала движения СG H и начала изменения CG H^lin (рис. 3, панель 1 ), разность ∆ t Hf = t Hf – t 2 между временами окончания движения СG H и окончания изменения CG H^lin (рис. 3, панель 2 ), разность ∆ t p = t 2 – t p между временами окончания изменения CG H^lin и достижения пика скорости изменения CG H (рис. 3, панель 3 ).

H -синергия

∆ t Hb , мс

100 г

70 I

30 I

∆ t Hf , мс

∆ t р , мс

Err , %

9r

6 I 3L

200 r

∆ t_cross , мс

–200 1

400 г

200 I

0I

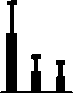
300 r

150 [

0I

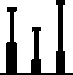
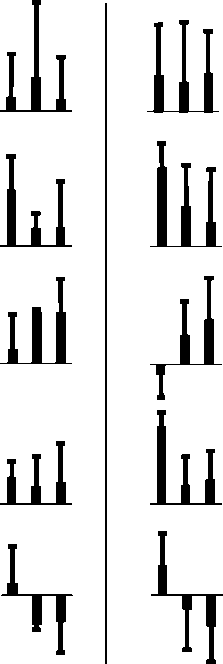
а б в а б в

ОС2       ОС3

а б в ОС1

Рис. 3. Усредненные по всем испытуемым (среднее± SD ) временные характеристики ∆ t Hb (1), ∆ t Hf (2), ∆ t р (3), ∆ t cross (5) сигналов прямого управления CG H^eq и CG А ⁰, а также среднеквадратичная ошибка Err (4) аппроксимации CG H^eq линейной функцией CG H^lin в процентах от амплитуды изменения CG_H ^eq . ОС1 – модель (8), ОС2 – модель (10), ОС3 – модель (11). Варианты а , б и в соответствуют трем методам расчета параметров петли обратной связи: а – решение обратной задачи динамики, б и в – решение прямой задачи динамики с минимизацией ошибки соответственно по скорости и положению центра тяжести CG_H

В среднем по всем испытуемым длительность движения по Н-синергии составила ∆tH = tHf – tHb = 622±80 мс. Как правило, начало движения tHb запаздывает по сравнению с началом t1 изменения CGHlin. Задержка ∆tHb = tHb – t1 для всех моделей ОС и методов расчета параметров ОС в среднем по всем испытуемым, моделям и методам оказалась небольшой ∆tHb = 54±51 мс, однако достоверно большей нуля (Т – тест, р < 0,001). Таким образом, начало изменения CGHlin почти совпадает с началом изменения CGH, что свидетельствует о том, что принятая линейная аппроксимация CGHlin хорошо улавливает начало изменения управляющего сигнала CGHeq и вызванное им начало движения. Остановка движения tHf тоже запаздывает по сравнению с окончанием t2 линейного аппроксимирующего отрезка. Это запаздывание также статистически достоверно (Т – тест, р < 0,001). В среднем по всем испытуемым, моделям и методам задержка составила ∆tHf = 165±178 мс. Отметим, что задержка ∆tHf значительно превосходит задержку ∆tHb, что согласуется с теорией РТ. Согласно данной теории задержка ∆tHb мала, так как связана только с инерцией биомеханической системы, приводящей к запаздыванию наблюдаемого перемещения тела по сравнению с началом изменения мышечных усилий. Напомним, что мышечные усилия возникают по причине рассогласования между начальной конфигурацией тела и его равновесной конфигурацией, изменяющейся в результате центральной команды. Задержка же ∆tHf велика, так как изменение CGHeq необходимо только для разгона движения, а торможение его происходит пассивно за счет «пружиноподобных» вязко-эластичных сил. Поэтому в теории РТ предполагается, что момент t2 окончания изменения CGHeq близок к моменту окончания разгона движения, т.е. к моменту tp достижения пика его скорости [9]. В наших экспериментах момент t2, как правило, был задержан относительно tp. В среднем по всем испытуемым, моделям и методам задержка составила ∆tр = 149±172 мс, т.е. 24% от полной длительности ∆tН движения по Н-синергии. Величина задержки ∆tр определяется соотношением между инерционными, вязкими и эластичными силами, и ее наличие не противоречит теории РТ.

Как видно из рис. 3 (панели 1 – 3 ), результаты, полученные методом решения прямой задачи динамики (варианты б и в ), в большинстве случаев близки для всех трех моделей ОС, в то время как результаты, полученные методом решения обратной задачи динамики (вариант а ), в среднем заметно отличаются от полученных методом решения прямой задачи. Поскольку ошибка аппроксимации управляющего сигнала CG H^eq с помощью CG H^lin меньше при использовании метода решения прямой задачи, чем обратной, рис. 3 (панель 4 ), то в рамках теории РТ метод решения прямой задачи является предпочтительным.

Тем не менее относительно небольшие значения ошибки свидетельствуют о том, что все рассмотренные модели и методы допускают хорошую аппроксимацию прямого управляющего сигнала CG H^eq с помощью простой линейной зависимости от времени CG H^lin , как это постулируется в теории РТ [9].

Сигнал прямого управления в А-синергии

Полное перемещение центра тяжести ∆ CG является суммой перемещений ∆ CG Н и ∆ CG А , связанных с движениями по Н - и А -синергиям. Перемещение ∆ CG А направлено вперед, «компенсируя» перемещение ∆ CG Н назад. В среднем по всем испытуемым ∆ CG А = 4,9±0,5 см, а ∆ CG Н = –3,9±1,0 см. Как и для Н -синергии, начало и окончание движения по А -синергии рассчитывались по пятипроцентному порогу от максимальной скорости перемещения центра тяжести в этой синергии. Для испытуемого, представленного на рис. 2, начало движения по Н -синергии опережало начало движения по А -синергии на 220 мс (рис. 2, в ). В среднем по всем испытуемым задержка начала движения по А -синергии относительно начала движения по Н -синергии составила t Аb – t Hb = 154±41 мс. Данный результат отличается от полученного авторами ранее в работе [5], где наблюдалось более раннее (в среднем на 70 мс) начало движения по А -синергии, чем по Н -синергии. Кроме того, в настоящей работе длительности движений по Н - и по А -синергиям оказались сравнимыми (в среднем по всем испытуемым: t Аf – t Ab = 636±200 мс и, как было приведено выше, t Нf – t Нb = 622±80 мс), в то время как в работе [5] длительность движения по А -синергии была значимо больше, чем по Н -синергии (820 мс по сравнению с 510 мс). Указанные отличия могут быть связаны с разными экспериментальными условиями. Во-первых, в работе [5] колени испытуемых не блокировались, а во-вторых, движения на неподвижной опоре не перемежались с движениями с возмущениями. Возможная адаптация к неожиданным возмущениям заключалась в задержке движения по А -синергии. Возможность такой избирательной адаптации движения по А -синергии служит еще одним дополнительным аргументом в пользу гипотезы авторов о независимом управлении А - и Н -синергий, высказанной в [2, 5, 6].

Как и для случая Н -синергии, параметры петли ОС, необходимые для расчета сигнала прямого управления ξ А ⁰ по уравнениям (12)–(14), для каждого из пяти испытуемых рассчитывались индивидуально. Использованные параметры были получены с помощью решения обратной задачи динамики и с помощью решения прямой задачи динамики с оптимизацией параметров петли ОС по скорости перемещения CG или по положению CG . Их значения, усредненные по всем испытуемым, приведены в работе [3].

На рис. 2, б жирной сплошной линией представлена типичная зависимость ξ А ⁰( t ) сигнала ПУ от времени, рассчитанная для одного из испытуемых методом решения обратной задачи динамики по модели ОС1. В отличие от случая Н -синергии коэффициент жесткости K А^S в петле ОС по А -синергии оказался близок к единице (в среднем по испытуемым, моделям и методам K А^S = 0,95±0,02). Таким образом, уравнение (9) для А -синергии неприменимо и любая конечная конфигурация тела, не приводящая к потере равновесия за счет выхода горизонтальной проекции CG за границы опоры, является приемлемой. Поэтому сигнал ПУ для А -синергии показан на графике не в терминах равновесного положения СG , как для Н -синергии, а в виде зависимости CG А ⁰ = b А ξ А ⁰.

Как показано на рис. 2, б , ход кривой для управляющего сигнала CG А ⁰ имеет две фазы, соответствующие разгону и торможению движения в данной синергии. В отличие от Н -синергии, в которой торможение движения обеспечивается «пассивными» вязко-эластичными силами, в А -синергии жесткости петли управления по ОС достаточно только для компенсации гравитационных сил. Поэтому торможение движения в данной синергии, как и разгон, происходит «активно», т.е. за счет прямого управления мышечными силами. Аналогично случаю Н -синергии (рис. 2, а ), начало движения t Аb запаздывает по сравнению с началом изменения сигнала прямого управления CG А ⁰ (рис. 2, б ). Как и для Н -синергии, эта задержка мала, так как связана только с инерцией биомеханической системы, приводящей к запаздыванию наблюдаемого перемещения по сравнению с началом изменения мышечных усилий. Окончанием фазы разгона и началом фазы торможения авторы полагали момент t cross перехода сигнала прямого управления CG А ⁰ через нуль (рис. 2, б ).

На рис. 3 (панель 5 ) представлены значения задержки окончания t cross фазы разгона по А -синергии относительно окончания t 2 изменения управляющего сигнала по Н -синергии ∆ t cross = t cross – t 2 для всех моделей ОС и методов расчета их параметров. В среднем по всем испытуемым, моделям и методам эта величина составила ∆ t cross = –48±175 мс и отличалась от нуля недостоверно (Т – тест, р = 0,07). Таким образом, окончание фазы разгона t cross движения по А -синергии фактически совпадает с окончанием фазы разгона t 2 движения по Н -синергии. При этом фаза разгона по Н- синергии полностью определяет конечную равновесную конфигурацию тела, а остановка движения в конечной конфигурации осуществляется «вязко-эластичными силами» петли ОС без участия активного ПУ. В отличие от этого, в А- синергии остановка движения осуществляется с помощью активного ПУ уже после завершения ПУ по Н -синергии.

Обсуждение результатов

Значения параметров петли обратной связи (ОС) при управлении движением тела стоящего человека в сагиттальной плоскости, рассчитанные в предыдущей работе авторов [3], были использованы в настоящем исследовании для анализа временного хода сигнала прямого управления (ПУ) при выполнении целенаправленного наклона корпуса вперед. Анализ проводился в рамках разработанного авторами ранее подхода к описанию движения в терминах «естественных синергий», или «собственных синергий» [4]. Последние определяются как движения вдоль собственных векторов уравнения движения для биомеханической модели тела человека в поле силы тяжести. Уникальным свойством естественных синергий является то, что в них сочетается простая линейная связь как между изменениями суставных углов (кинематическая синергия), так и между изменениями суставных моментов (динамическая синергия). В настоящей работе движения в коленных суставах блокировались и, таким образом, использовалась модель тела с двумя суставами – голеностопным и тазобедренным. В этом случае существуют две естественные синергии. По доминирующему суставу, дающему максимальный вклад в динамику и кинематику каждой из них, они были названы «Н-синергией» (Hip – тазобедренный сустав) и «А-синергией» (Ankle – голеностопный сустав). Ранее авторами было показано, что естественные синергии независимо друг от друга управляются как напрямую [1, 5], так и по обратной связи [2, 3, 6].

В физиологии движений существуют две точки зрения на организацию двигательного управления в живых системах. Согласно одной из них эта организация основана на управлении равновесным положением (равновесной конфигурацией) биомеханической системы. Согласно второй – она основана на непосредственном прямом управлении силами мышц.

Первая точка зрения наиболее последовательно представлена в теории равновесной точки (РТ) [9]. Согласно этой теории при выполнении движения планируется только равновесная конфигурация тела, в то время как переход из начальной конфигурации в конечную осуществляется за счет «пассивных вязкоэластичных сил», определяемых петлей ОС по рассогласованию между действительной и планируемой конфигурациями тела. Преимуществами такого подхода являются, во-первых, то, что движение планируется в терминах статики, а его динамика обеспечивается «автоматически» по петле ОС, и, во-вторых, то, что конечная конфигурация достигается и при неожиданных возмущениях во время выполнения движения.

Согласно второй точке зрения, представленной, например, в работе [12], движение планируется в терминах изменения мышечных сил, обеспечивающих желаемую траекторию и скорость движения вдоль этой траектории. При этом непосредственное управление мышечными силами осуществляется путем решения обратной задачи динамики с помощью внутренней нейронной модели (ВНМ) [16, 23], учитывающей схему тела и инерционные характеристики его звеньев. Преимуществом данного подхода является возможность планирования не только простого перемещения из начального положения в конечное, как постулируется в теории РТ, а любого сколь угодно сложного движения. Недостатком двигательного управления, основанного на таком принципе, является невозможность достижения желаемой конечной конфигурации без коррекции сигнала ПУ в том случае, если во время двигательного акта происходят неожиданные внешние возмущения. Это объясняется преуменьшением роли обратной связи в рамках данного подхода.

Как показано выше в разделе «Модель и методы», в принятом авторами линейном приближении для модели петли ОС на биомеханическом уровне обе точки зрения на организацию двигательного управления формально приводят к одинаковым выражениям для управляющих сил (суммарных силовых моментов в суставах). Поэтому вопрос о предпочтении первой или второй точки зрения сводится к оценке того, достаточно ли велики «вязко-эластичные силы» (коэффициенты жесткости и вязкости в петле ОС), чтобы обеспечить наблюдаемое движение при простом законе изменения сигнала прямого управления [13]. Например, в теории РТ постулируется, что сигнал ПУ изменяет равновесную конфигурацию тела с постоянной скоростью вдоль прямой траектории, соединяющей начальную и желаемую конечную конфигурации тела [9]. Когда «вязко-эластичные силы» достаточны для выполнения движения с таким «простым» сигналом ПУ, можно принять, что для рассматриваемого движения осуществляется «статическое» ПУ согласно теории РТ («управление по положению»). Если же «вязко-эластичные силы» недостаточны и требуется непосредственное управление силами мышц, то можно принять, что осуществляется «динамическое» ПУ согласно теории ВНМ («управление по движению») [13].

Результаты настоящего исследования показывают, что при выполнении наклона корпуса в сагиттальной плоскости у человека наблюдаются оба типа организации двигательного управления. Как отмечалось выше, данное движение является суперпозицией двух независимых «естественных синергий». При этом управление по Н -синергии организовано по первому типу (хорошо согласуется с теорией РТ), а управление по А -синергии – по второму типу (согласуется с теорией ВНМ). Коэффициенты жесткости и вязкости петли ОС для Н -синергии оказались достаточно велики, чтобы выполнить движение по этой синергии при «простом» линейном характере изменения сигнала прямого управления (см. рис. 2, а , тонкая сплошная линия). Отметим, что жесткость в петле ОС для Н -синергии возрастает во время выполнения движения по сравнению со случаем неподвижного вертикального стояния [3]. В отличие от этого, коэффициент жесткости в петле ОС для А -синергии во время движения оказался меньше, чем при неподвижном стоянии [3]. При этом во время движения коэффициент жесткости К A^S близок к единице, т.е. достаточен лишь для уравновешивания гравитационных сил. В этом случае любая конечная конфигурация тела в А -синергии, при которой проекция центра тяжести остается в пределах площади опоры, является нейтрально устойчивой. Если во время выполнения наклона корпуса происходит неожиданное кратковременное возмущение движения, то желаемая конечная конфигурация тела в Н -синергии все-таки достигается, несмотря на возмущение, в то время как в А -синергии возмущение изменяет конечную конфигурацию тела [3].

В случае наклона корпуса Н -синергия обеспечивает целевую компоненту движения – наклон на заданный инструкцией угол, а А -синергия обеспечивает вспомогательную постуральную компоненту движения, которая компенсирует смещение центра тяжести по целевой компоненте [5, 18]. Поскольку инструкция задавала амплитуду наклона корпуса , почти полностью определяемую движением по Н -синергии, то управление по этой синергии происходит «по положению» (в соответствии с теорией РТ), что согласуется с наблюдаемым во время движения увеличением жесткости K H^S . Конечное же положение центра тяжести явно инструкцией не задается (очевидно, что его проекция для сохранения равновесия должна лишь оставаться в пределах площади опоры), поэтому оно и не является объектом точного контроля со стороны ЦНС. При неподвижном стоянии поведенческой задачей, очевидно, является поддержание заданной конфигурации тела как по Н -, так и по А -синергиям, и поэтому двигательный контроль в этом случае организован «по положению» по обеим естественным синергиям. Соответственно, коэффициент жесткости по А -синергии при неподвижном стоянии ( K A^S ≈ 1,0–1,15, [2, 3, 6]) оказался больше, чем при выполнении наклона корпуса ( K A^S = 0,95, [3]), обеспечивая более устойчивый, чем при движении , контроль заданного неподвижного положения и по А -синергии [6].

Ранее особенности организации управления движением при наклоне корпуса человека исследовались в рамках теории РТ в работе [7]. Было показано, что паттерн изменения равновесного угла в тазобедренном суставе в зависимости от времени имеет немонотонную N -образную форму. Такой характер изменения равновесного угла отличается от полученного в данной работе для Н -синергии, изменение которого оказалось монотонным в согласии с более принятым представлением в теории РТ.

Данное расхождение, по-видимому, объясняется тем, что в работе [7] исследование проводилось в терминах контроля силового момента в тазобедренном суставе в зависимости от угла в этом суставе. В то же время, как показано в работах авторов [2– 6], при выполнении наклона контролируются не отдельные суставы, а «естественные синергии», в каждую из которых дают вклад все суставные углы. Более того, в настоящей работе показано, что только движение по Н -синергии можно трактовать в рамках теории РТ, в то время как движение по А -синергии не согласуется с этой теорией.

Отмеченные особенности организации двигательного управления по Н - и А -синергиям наблюдались для всех трех рассмотренных моделей петли ОС и не зависели от метода расчета их параметров.

Результаты настоящего исследования показывают, что обе упомянутые выше точки зрения на организацию управления движениями в живых системах (либо «по положению», либо «по движению») не столько противоречат, сколько дополняют друг друга. Выбор способа управления зависит от поведенческой задачи. Более того, в одном двигательном акте, примером которого является рассмотренный авторами наклон корпуса в сагиттальной плоскости у человека, оба способа управления могут наблюдаться одновременно.

Благодарности

Авторы выражают глубокую благодарность профессору Ж. Масьону за помощь в проведении эксперимента и обсуждении результатов.

Настоящее исследование поддерживалось грантами РФФИ 10-04-00191-а, РГНФ 09-06-00883-а, а также программой РАН «Фундаментальные науки – медицине».