Осаждение двух частиц в параболическом потоке

О. А. ПЕТУХОВА, кандидат физико-математических наук

Рассмотрим осаждение двух твердых сферических частиц А и В одинакового радиуса, которые помещены в неограничен ную несжимаемую вязкую жидкость. Считается, что размеры частиц достаточно малы, так что число Рейнольдса меньше едини

цы. Скорость жидкости на бесконечности U есть квадратичная функция координат

^i — Су^х^х^ C_iik = С^ — 0.

В работе [1] показано, что поведение частиц в параболическом течении существенно иное, чем в линейном течении. Существует такое положение сферы В, при котором относительная скорость сфер Uj = 0. Другими словами, частицы, находящиеся в плоскости, проходящей через ось параболического профиля скоростей, и на одинаковом расстоянии от этой оси, имеют одинаковые скорости. Причем это положение устойчивое: если частица В располагается ближе к оси, чем частица А, то она взаимодействует с А с силой отталкивания, и наоборот, частица В притягивается к А, если она находится дальше от оси.

Таким образом, две частицы в параболическом потоке стремятся оставаться в плоскости, проходящей через ось симметрии течения, и на одинаковом расстоянии от оси. Одна из них приближается к оси, а другая удаляется от нее. В данном случае центр масс двух частиц будет на оси симметрии течения. В линейном поле скоростей подобное поведение частиц не на блюдается, что обусловлено различными свойствами решений для течений со скоростями, представляемыми на бесконечности в виде полиномов четной и нечетной степеней.

Представляет интерес вопрос о том, как быстро частицы приходят к положению устойчивого равновесия. Для этого необходимо решить систему дифференциальных уравнений

^Uayt = 0, ra=raQ, at

^; = U^b, t = 0, r_b = r_b0.

L at

Здесь U^a ,U^b — скорости частиц, полученные в [2].

Решение системы искалось численно при помощи программы «Математика». Результаты оформлялись графически.

Зависимость координат положения центров частиц A(xl, yt, г!) и В(х2, у2, z2) от времени в случае, когда направления течения жидкости и вектора ускорения свободного падения противоположны, представлена на рис. 1—4.

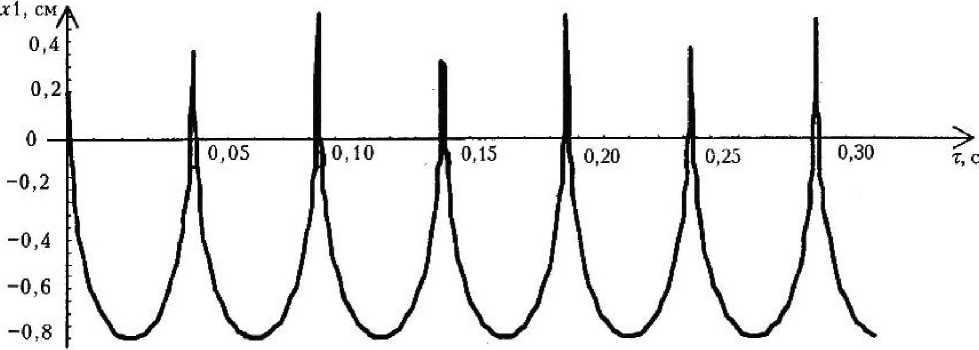
Р и с. 1. Изменение координаты zl центра частицы А при начальных условиях т!(0) ~ 0,2 см, х2(0) = 0,9 см, т = 0 - 0,3 с

0,900

0,875

0,850

0,825

0,800

0,775

х2, см^ 0,925

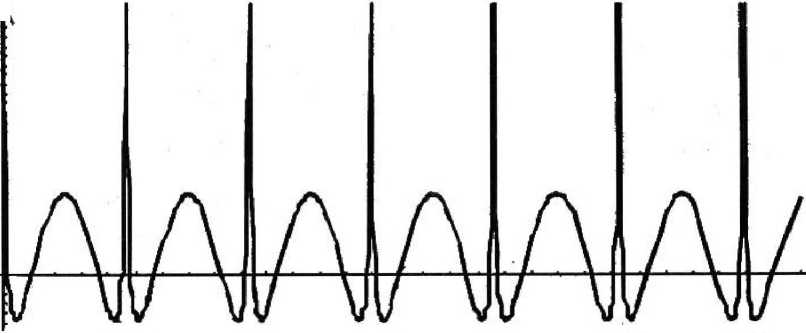
0,05       0,10       0,15       0,20       0,25       0,30

г, с

Р и с. 2. Изменение координаты х2 центра частицы В при начальных условиях хКО) = 0,2 см, х2(0) = 0,9 см, т = 0 — 0,3 с

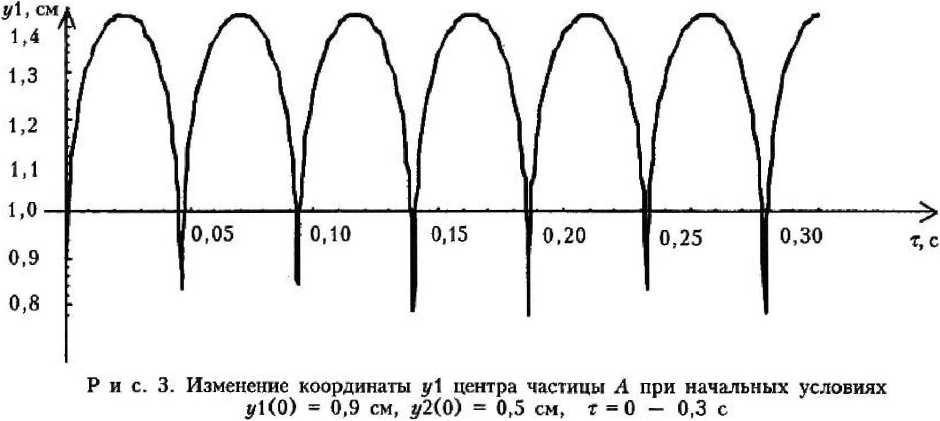
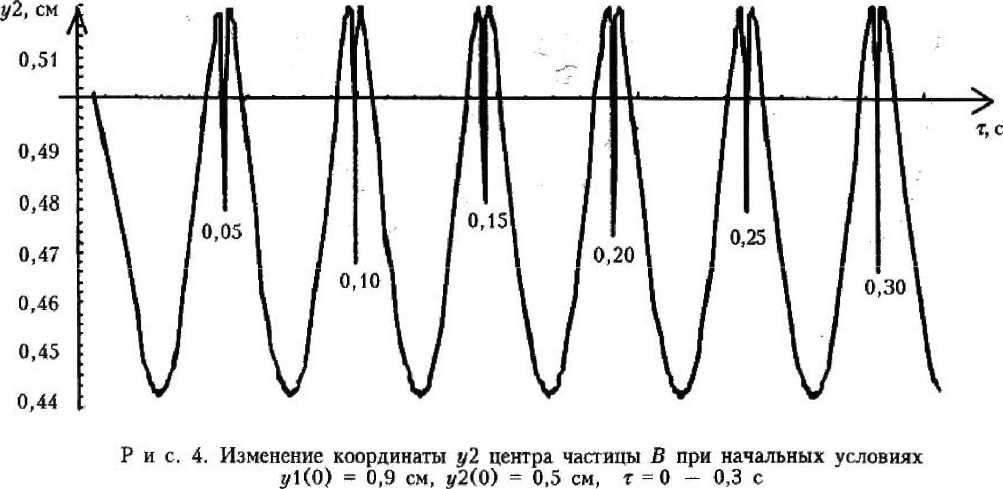
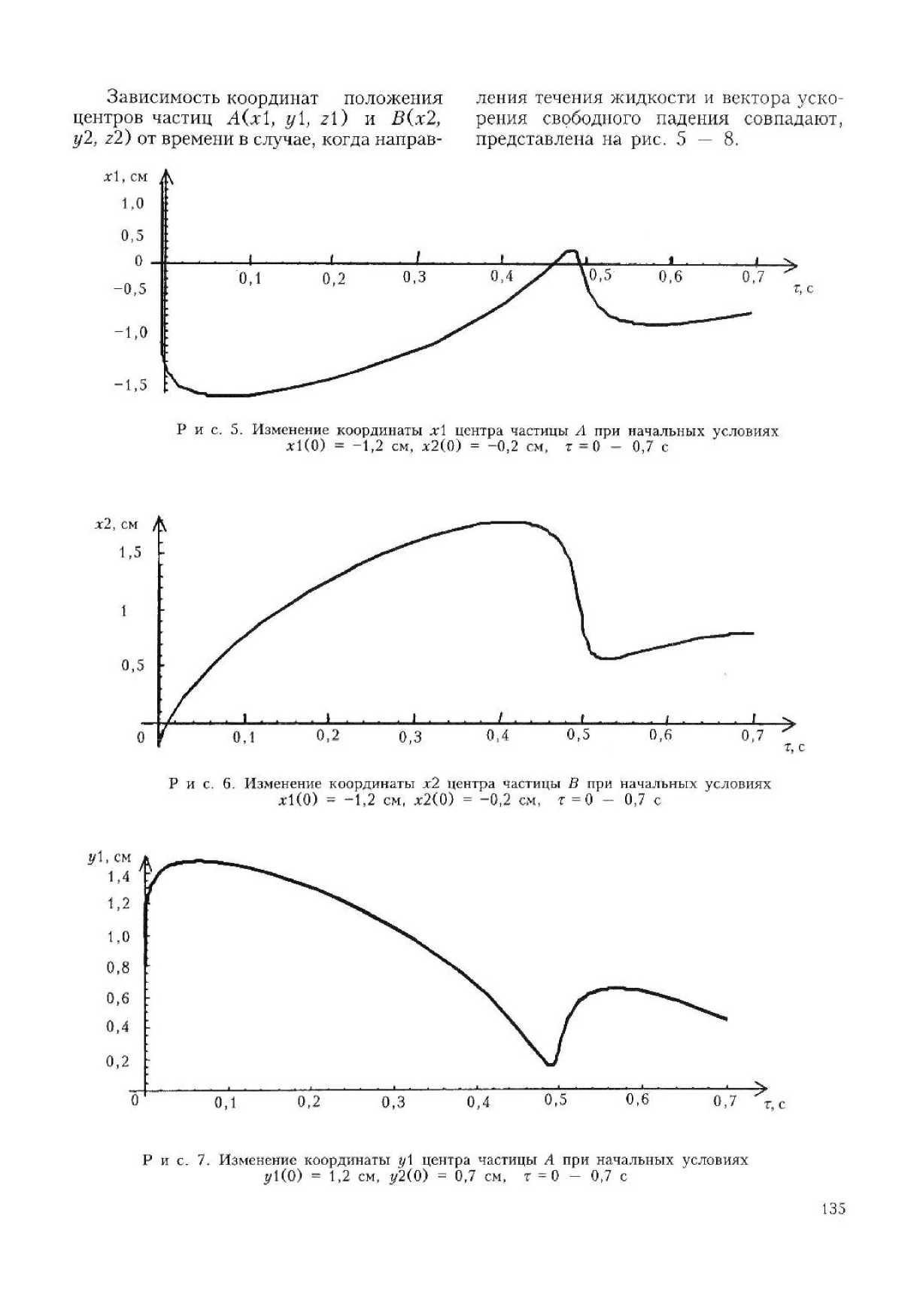
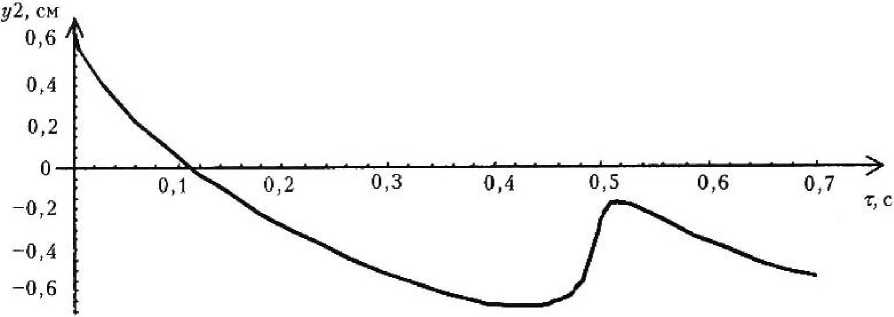
Рис. 8. Изменение координаты у 2 центра частицы В при начальных условиях у!(0) -1,2 см, 5/2(0) = 0,7 см, т = 0 — 0,7 с

Аналогичный результат для относительных скоростей сфер получается, если на сферы действует не сила тяжести, а какая-либо другая потенциальная сила, например со стороны магнитного поля. При этом магнитные силы, действующие на частицы, должны быть одинаковы, что возможно, когда немагнитные частицы находятся в сильном неоднородном магнитном поле.