Осесимметричное деформирование толстостенной стесненной оболочки под внутренним давлением при нелинейном законе деформационного упрочнения

В широкой практике достаточно часто встречаются материалы, при упругопластическом деформировании которых имеет место физическая нелинейность, которая проявляется в нелинейном законе деформационного упрочнения при описании диаграммы деформирования. В немногочисленных трудах рассматриваются вопросы физической нелинейности. Особенно важным данный вопрос представляется для толстостенных оболочек, работающих под давлением. В частности, в работе [1] рассмотрено пластическое деформирование толстостенного цилиндра внутренним давлением при произвольном законе упрочнения и с использованием условия пластичности Треска. Вопросы расчета напряженно-деформированного состояния цилиндрических оболочек в условиях неоднородности и физической нелинейности рассматривались в трудах [2, 3]. Сегодня проблеме деформирования оболочек в форме тел вращения уделяется достаточно много внимания. Неклассические математические модели деформирования оболочек и численные методы их расчета исследовались в трудах [4, 5]. Некоторые решения задачи Ламе для цилиндрической оболочки рассматривались в работах [6, 7]. Деформирование осесимметричных оболочек в условиях комбинированного нагружения исследовались в трудах [8–10]. Многие из этих задач рассматривались для моделей жесткопластического тела, а также для моделей материала без упрочнения, в частности, работы [11, 12]. В некоторых задачах данные упрощения обоснованны, однако для многих материалов неучет упругих деформаций, а также упрочнения может приводить к значительным погрешностям в расчетах напряженно-деформированного состояния толстостенных оболочек.

В рамках данного исследования рассматривалось упругопластическое деформирование стесненной толстостенной оболочки из несжимаемого материала, работающей под внутренним давлением. Особенностью напряженно-деформированного состояния стесненной оболочки является то, что она находится в условиях плоской деформации. Ряд вопросов математического моделирования пластического состояния тел в условиях плоской деформации исследовались в работах [13–15].

В работе [16] представлено решение задачи о деформировании толстостенной стесненной цилиндрической оболочки под внутренним давлением, но для модели идеального упругопластического тела. В условиях же физической нелинейности расчет напряженно-деформированного состояния оболочек представляет собой сложную математическую задачу и требует разработки численных процедур. В рамках данного исследования численный расчет напряженно-деформированного состояния осесимметричной оболочки проводился при нелинейном законе деформационного упрочнения.

Андрианов И.К.

Методика исследования

Решение задачи осесимметричного упругопластического деформирования толстостенной оболочки под внутренним давлением будем проводить на основании положений линейной теории упругости и деформационной теории пластичности с использованием метода переменных параметров упругости [17–20]. Учитывая то, что цилиндрическая оболочка находится в условиях равномерного нагружения, расчет будем проводить в главных осях. В качестве меры деформации будем использовать деформацию Генки. Стесненная цилиндрическая оболочка представляет собой цилиндр с закрытыми торцами, соответственно, в результате нагружения оболочка находится в условиях плоской деформации: e zz = 0, где e _zz - осевая деформация Генки. Поскольку рассматриваемый материал является несжимаемым, коэффициент поперечной деформации принимается р = 0,5.

Математическая постановка задачи упругопластического деформирования толстостенной цилиндрической оболочки из несжимаемого материала в условиях плоской деформации будет описываться следующей системой уравнений:

– уравнение равновесия:

РР + РР ° _ 0 dp       р      ’

где °_pp,° oo — радиальные, окружные напряжения, р - радиальная координата.

– уравнение совместности деформаций Генки [17–20]:

deoo   1 - exP (eoo - epp), dp         p       ’ где eρρ ,eθθ – радиальные, окружные деформации Генки, – физические соотношения согласно методу переменных параметров упругости:

^epp =4F ⁽ ° pp ^- ° ⁰⁰ )

e^{eoe _} 43Г (°^{0 0 -} ° pp ) ’

° zz = ( ° pp ⁺ ° oo ) /2

где ° _zz - осевые напряжения, E = ° il e i - переменный параметр упругости при условии несжимаемости материала, σ – интенсивность напряжений, e – интенсивность деформаций Генки:

°i = 3°\°OO - °pp|, ei = 3 УР^ + eppeOO + eO)O ,

– диаграмма деформирования:

°i_ Ф (ei), где Ф(ei) = {Eei,ei eim} - функция, аппроксимирующая диаграмму деформирования материала, eiт – интенсивность деформаций Генки, соответствующая переходу упругих деформаций в пластические, E – модуль Юнга материала, A,n – параметры кривой упрочнения диаграммы деформирования,

– условие пластичности Мизеса:

° i = ° т ,                                         (7)

где σ _т – предел текучести материала, – граничные условия:

° рр\р = r ^_- Р,                                        ⁽⁸⁾

Механика

° Pp\p = R   ⁰,

где p – давление, r – внутренний радиус оболочки, R – наружный радиус оболочки.

Для проведения численного расчета представим уравнение совместности деформаций (2) в интегральной форме, выражая окружную деформацию Генки с учетом граничного условия (8):

R

e00

■00

R 1

= In - p J —exp ( 2 e_t P P

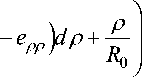
где R ₀ – начальный радиус наружной поверхности оболочки.

Подставим в соотношение (10) физические уравнения (3) для eρρ и eθθ. Тогда, выразив окружное напряжение, интегральное уравнение совместности деформаций Генки, представленное в напряжениях для несжимаемой толстостенной цилиндрической оболочки с закрытыми концами, примет вид:

p 1

- P f ~exp

R P

9     _ 4 E 0	91
	4 E p

R

J ^dpdp + ^P .

1 P ,    4. ,

° ee =- ⁴ 00^d P + r E In

Pr       ³

Численный расчет системы уравнений (1)–(11) проводился на основании метода переменных параметров упругости с использованием методики решения серий обратных задач [17–20], которая строилась на смещении наружного края оболочки на малую величину согласно соотношению R = R0 + AR и расчете напряженно-деформированного состояния, при котором произошло данное смещение. Таким образом, для численного расчета напряженного состояния оболочки итерационная система уравнений согласно соотношениям (1), (3), (4), (11) принимала вид:

1 R             л         ( R 1          и

-9   1 Г ( k h j , P

--40 ’dpdp + — 4 E ^{( k} ) P           R

(k+1)     1 г (k) ,      4    (k)               1              9

40     \40 ^dP ⁺ 7 ^{E ;}l^{n -} P j —exP -Г4440 ’

P           3             P2

p                   < pp     l7

~ ^{(k    1} ^' ^{k + 1 )} dP^ z ^(k    J (^ pp^ ^{+ 1 )} + ^«' ^{k + 1 )}) 4 , ’ ^k    у (^' ^{k + 1 )} — d ^{k +1 )}).

pP                       2'<2v где k – номер итерации.

Деформированное состояние оболочки определялось согласно уравнениям (3), (5) на текущей итерации:

_e ( ^k +1)₌    ³   [ _ ( ^k +1 ), ( ^k +1 )K( ^k +1)₌    ³   [ _ ( ^k +1 )-^ ( ^k +1 )1

epp    4E (k)4pp     40    )’e00    4E (k)(40     4pp    )’ e (k+1) - 2    (k+1) ? + ekk+1Mk+1Ые(k+1) V ei    =3v ePP  ) + ePP e00  +(e00 ) .

На основании соотношения (6), описывающего диаграмму деформирования материала, определялся переменный параметр упругости: E (k+1) = Ф(e,(k+1))/e,(k+1). Далее итерационный расчет повторялся до тех пор, пока не выполнится условие: 4/k+1) - 4,(k) / 4(k+1) < A4 где Ad - заданная точность. Расчет внутренней границы определялся согласно схеме

r ⁽ j ^{+1 )} = r ₀exp I e₀⁽ j )     I, где j - номер итерации, r ₀ - начальный радиус внутренней поверхно-

^      p = r 7

сти оболочки, r ⁽ j ⁺¹ ) - r ⁽ j ) / r ⁽ j ⁺¹ ) < A r - условие окончания процесса, A r - заданная точность.

Затем приложенное давление p определялось согласно граничному условию (8).

Результаты исследования

Для оценки напряженного состояния толстостенной цилиндрической оболочки с закрытыми концами, находящейся под внутренним давлением, были проведены серии численных расчетов

Андрианов И.К.                          Осесимметричное деформирование толстостенной стесненной оболочки под внутренним давлением … при следующих относительных толщинах стенки: 8/ R = {0,1; 0,2; 0,3; 0,4; 0,5}, где 8 - толщина оболочки, наружный радиус принимал фиксированное значение R = 100 мм. В качестве материала оболочки использовалась сталь марки ЗОХГСН2А (E = 195 ГПа, ст = 1110 МПа) [21]. Диаграмма деформирования стали 30XГCH2A описывалась линейно-степенной аппроксимацией (A = 4623, n = 0,276). Для того чтобы оценить распределение напряжений в упругопластической стадии деформирования, внутреннее давление для оболочки каждой толщины подбиралось таким образом, чтобы цилиндрическая поверхность, разделяющая область пластических и упругих деформаций рт = рс =с , совпадала со срединной поверхностью р = (R + r)/2. В этом случае внутреннее давление для оболочек различной толщины принималось p/ст ={0,119; 0,248; 0,394; 0,563; 0,775}. Результаты расчета напряженного состояния оболочки при упругопластическом деформировании с учетом степенного деформационного закона упрочнения представлены на рис. 1–4.

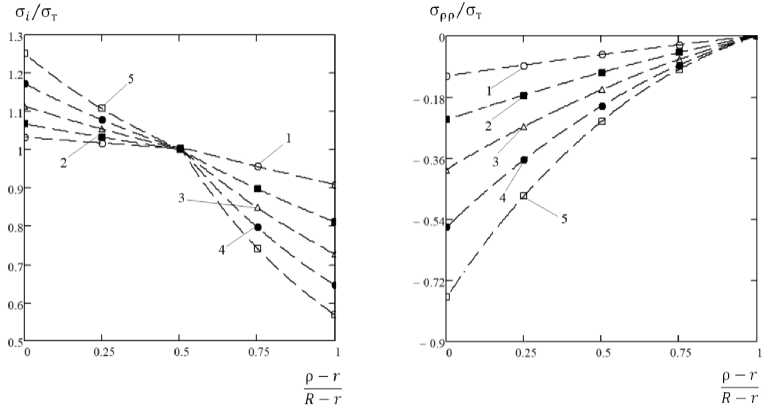
Рис. 1. Распределение интенсивностей напряжений по толщине оболочки при Р т = ( ^R + ^r ) ^{/2 :}

1 - 8 / R = 0,1, 2 - 8 / R = 0,2, 3 - 8 / R = 0,3,

4 - 8 / R = 0,4, 5 - 8 / R = 0,5

Рис. 2. Распределение радиальных напряжений по толщине оболочки при Р т = ( ^R + ^r ) ^{/2 :} 1 - 8 / R = 0,1, 2 - 8 / R = 0,2, 3 - 8 / R = 0,3, 4 - 8 / R = 0,4, 5 - 8 / R = 0,5

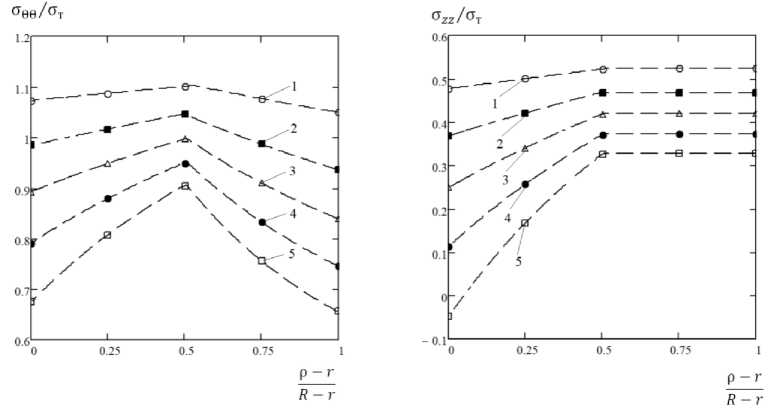
Рис. 4. Распределение осевых напряжений по толщине оболочки при р т = ( R + r ) /2 : 1 - 8 / R = 0,1, 2 - 8 / R = 0,2, 3 - 8 / R = 0,3, 4 - 8 / R = 0,4,

Рис. 3. Распределение окружных напряжений по толщине оболочки при р т = ( R + r ) /2 : 1 - 8 / R = 0,1, 2 - 8 / R = 0,2, 3 - 8 / R = 0,3, 4 - 8 / R = 0,4,

5 - 8 / R = 0,5

5 - 8 / R = 0,5

Механика

Обсуждение результатов

Согласно полученным результатам численных расчетов, с увеличением относительной толщины стенки оболочки радиальные сжимающие напряжения, при которых половина толщины стенки переходит в стадию пластического деформирования, возрастают по абсолютной величине, достигая наибольшее значение на внутренней границе оболочки. Окружные растягивающие напряжения, при которых половина толщины стенки оболочки переходит в стадию пластического деформирования, с увеличением относительной толщины стенки уменьшаются. При этом по толщине стенки окружные напряжения изменяются по нелинейному закону в упругопластической стадии, достигая максимум в срединном сечении стенки оболочки, соответствующем переходу упругих деформаций в пластические. В упругой стадии окружные напряжения уменьшаются, а в пластической стадии – увеличиваются. Осевые напряжения в пределах пластических деформаций возрастают по толщине стенки оболочки, а в пределах упругих деформаций остаются постоянными. С увеличением относительной толщины стенки оболочки осевые напряжения, при которых половина толщины стенки переходит в стадию пластического деформирования, уменьшаются. В пластической стадии деформирования интенсивности напряжений, при которых половина толщины стенки переходит в стадию пластического деформирования, возрастают с увеличением относительной толщины стенки оболочки, а в упругой стадии – с уменьшением относительной толщины стенки.

Заключение

Полученные в рамках данного исследования результаты позволяют рассчитать напряженно-деформированное состояние толстостенной стесненной цилиндрической оболочки из несжимаемого материала, находящейся под действием внутреннего давления, в том случае, если диаграмма деформирования материала в пластической стадии описывается нелинейным законом деформационного упрочнения. Построенные графические зависимости позволяют оценить в зависимости от изменения относительной толщины стенки оболочки характер изменения окружных, радиальных и осевых напряжений, возникающих при упругопластическом деформировании, когда пластическая зона охватывает половину толщины стенки оболочки, что может быть использовано в задачах автофретирования.

Исследование выполнено за счет гранта Российского научного фонда №25-79-10135,