Осесимметричный изгиб круглой многослойной пластины на упругом основании сложной структуры

Простейшая осесимметричная задача контактного взаимодействия как для слоистого, так и непрерывно-неоднородного покрытия упругого полупространства рассмотрена в работе [4]. Задача об изгибе пластины на упругом изотропном и однородном основании рассматривалась в работах [5, 6]. Решение строилось путём представления контактных напряжений в виде степенного ряда, с последующим определением коэффициентов разложения из бесконечной алгебраической системы уравнений.

Методом ортогональных многочленов такая задача решалась в работах [7, 8], а методом коллокации по чебышёвским узлам — в работах [9,10]. При этом возникала необходимость построить решение некоторых бесконечных систем линейных алгебраических уравнений и ставилась проблема исследования сходимости полученного решения к точному. В работах [11,12] для решения задачи применялись асимптотические методы типа «больших Л» и специальных ортогональных многочленов, что позволило получить основные характеристики решения в нескольких формах, каждая из которых эффективна в своей области изменения характерных параметров задачи.

Результаты работы получены при выполнении проекта, поддержанного грантом РФФИ № 13-08-90916-мол_ин_нр.

Отметим, что большинство известных решений эффективны только для жёстких пластин. И очень немногие, в частности, представленные в [11, 12], эффективны или для гибких, или для жёстких пластин, каждое в своей области.

Интерес к решению задачи и её актуальность сохраняется и в настоящее время. Так, в работе [13] решение строилось с использованием разложения напряжения в двойной ряд Фурье. Аналогичный подход использовался в работе [14]. Andrea R. D. Silva с соавторами развил численные методы решения задачи [15]. В работе [16] было получено приближённое аналитическое решение осесимметричной задачи об изгибе пластины со свободным краем, лежащей на функциональноградиентном основании. Для этого использован двусторонне асимптотический метод [17].

В настоящей работе метод [17] использован для решения задачи об изгибе многослойной пластины.

Постановка задачи. Круглая многослойная пластина радиуса R и постоянной толщины h лежит на поверхности z = О упругого полупространства, состоящего из неоднородного мягкого слоя (покрытия) толщины Н (-Н ,z; координата г отнесена к радиусу пластины R, координата z— к толщине покрытия Н, ось z нормальна поверхности и проходит через центр пластины. Под действием осесимметричной распределённой нагрузки р* (г) и реакции со стороны слоя пластина изгибается. Прогиб пластины обозначается функцией и/* (г).

Коэффициенты Ламе мягкого слоя меняются с глубиной по закону:

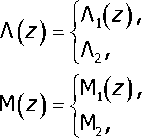
1 < z < О,

■со < Z < -1,

-1 < z < О,

-со < Z < -1.

При расчётах для задания характера неоднородности покрытия удобно использовать модуль Юнга, а коэффициент Пуассона зафиксировать и считать постоянным. Известно [18], что

5_мЗА + 2М

А + М '

А

V = —;--

В качестве параметра, характеризующего отличие упругих свойств слоя от подложки, введём величину

где Е_г (z) и Е_г — модули Юнга покрытия и подложки соответственно.

Уравнение изгиба многослойной пластины имеет вид:

^,(/'W+i(/'W-i(r)' 0<г<1,                  (2)

где Ц

' Vdr2 + rdr)

дифференциальный оператор изгиба Ай пластины; q* (г) — контактные

напряжения под пластиной; и/, (г) — прогиб каждого слоя; О, — цилиндрическая жёсткость Ай пластины.

Для напряжений, возникающих между слоями пластины, выполнено следующие условие сопряжения:

М7')^7')' 0<г<1.                     (3)

Если все слои жёстко сцеплены друг с другом, то w_x (г) = и/₂ (г) =... = w_K (г) = и/* (г). Учитывая это обстоятельство, а также равенство (3), система уравнений (2) может быть представлена в виде: к           ( 1 ri

DL₆vrVWVWArV№D^D^^^^ /=1           уиГ    / UI

, 0<г<1.         (4)

Таким образом, вместо многослойной платины можно рассматривать однослойную пластину с цилиндрической жёсткостью, равной сумме цилиндрических жёсткостей каждого слоя в многослойной пластине.

Если пластина неоднородна по толщине, её модуль Юнга Е_пп (z) при этом изменяется по толщине пластины, а коэффициент Пуассона v_m постоянный, то, согласно [19]:

° = т^^^2Е.А^.                  (5)

1 "пл О

Введём следующую замену переменных: X = H/R, и/* (г) = w (r'^R, р* (г) = p^r'^DR ³

q* (г) = q (r'^DR ³. Знак штриха далее опускаем.

Рассматривается два случая граничных условий: первый, когда края пластины закреплены, в этом случае функция прогиба пластины w^r) удовлетворяет условиям:

0W dr

= 0, —(Ди/)

8гх 7

= 0,

и второй случай, когда имеют место условия свободного края:

32и/ vnjl 8w dr2 г Эг

= 0, —(Ди/)

Qrv 7

= 0,

где vm — коэффициент Пуассона пластины; Д — оператор Лапласа.

Методом интегральных преобразований контактная задача сводится к решению системы уравнений:

L_owQ^ = pQ^-qQ^, 0<г<1,                     (8)

|Q(a)A(aA)J₀ (ar^da =sw(r), 0<г<1,

(9) fQ(a)J_o(ar)tfa = O, г>1, .0

где А (и) — трансформанта ядра; s = ©R3 [У1 — параметр, характеризующий изгибную жёсткость пластины

Построение решения. Для однородной пластинки со свободными краем, лежащей на неоднородном полупространстве, в работе [16] построено решение задачи в аналитическом виде. Учитывая (4), (5), это решение можно использовать и для неоднородных пластин.

Построим решение задачи в аналитическом виде, в случае, когда края пластины закреплены. Для этого представим функцию прогибов в виде ряда по формам собственных колебаний круглой пластины с закреплённым краем, аналогично работе [20]:

СО 1

W(r)=IX^m(4 Wm = ^(р)ф„,(р)РСф, (10) m=0 о где Фт (И = 4 Л 1кЛ; 4 - корни уравнения Л (4) = 0, а 4 = V2 / Jo (4) для m е N.

Учитывая линейность задачи, разложим функцию контактных напряжений (Хг) в ряд следующего вида:

(И)

/77=0

Здесь функции q_m (г) находятся из решения парного интегрального уравнения (9) с заданной правой частью вида (10).

Для построения решения рассмотрим следующее парное интегральное уравнение:

J Q ^1 (аЛ) J_o (ог)/Уо = 06 1 + £ u_k J_o (р^г) , 0 <  г < 1, о                       V И         7

fQ(o)J₀ (аг)/7а = 0, г >1.

Из результатов работы [21] следует, что при построении решения задачи двухсторонне асимптотическим методом в качестве аппроксимации главной части трансформанты ядра можно использовать аналитическое выражение вида

4 4+а,2

У и2 + Д2'

где b_k , р^, б — некоторые константы.

В работе [22] получено аналитическое решение парного интегрального уравнения (12) в виде:

T(r) = ^oWL-i(O)^U + f

^П L <1-г    '=1

Здесь введено обозначение:

Ф(г,/1) = -Е^

г sh/iyf

Сумма в (14), содержащая функцию Ф^/р), соответствует решению уравнения (12) с правой частью в виде ряда по функциям Бесселя. Функцию фт (г) можно представить в следующем виде:

Ф™ (/'М^ Л(мГг)

ГЛА I — А ■ I i^m — где и_х -        - к_т.

Таким образом, решение парного интегрального уравнения (9) с правой частью (10) имеет вид:

Qo О') = 2 V^s U (0) (1 - г²)^{1 2}

/V

+ ГС^(г/а/Л1)

ч“(Н^~‘АЛ^к„)Ч^^           , m = l,2,

Здесь постоянные C,m определяются из системы линейных алгебраических уравнений:

/V ycMa^\b^VW^ =0' k = l,2,...,N, /=1

/V

УС,та(аХ1,дЛ1) + 3(^,^Л1) = 0, k = 1,2,...,/V; т = 1,2,..„ \  /      * К )    • \ Гн • К у *             i i i i где uia,иi — i asna + иcnajiи —a i , pia,Di — lw (Aaiu(/a,oi

Полученные значения контактных напряжений ^ (г) и заданную внешнюю нагрузку, приложенную к пластине, можно представить в виде следующих рядов:

^(г) = £кГф7(г), у; =J^(p)v7(p)pt/p,(is)

7=0О

СО

т=0о

Подставив разложения (10), (15), (16) в (8), придём к бесконечной системе линейных алгебраических уравнений для определения коэффициентов wm, которую можно записать в следу ющем виде:

^m-ak^w₃^ =р_тк^, m = 0,1,2,...; а = -1. 7=0

Ет _ Э|-|-1 /1 r-Л Г/-1 ( Y \ \z (\ ।                           \ у — 2п A^s^ yLN ^ЛКуJхук^fkm)-v^Cn X^а^л ,ктJ п=0                          .

где 7=1,2,...; т =0,1,2,...;

х (a, b) = b^A ^cos a sin b +1- ^sin (а - Ь) (а - Ь) ¹ - sin

X(a,b) = (a² +b²) ^ashacos^ + ^sinscha).

В частности,

Г-                               N        /

₀ — 2п ^25^ ц, (0)к_т sin к_т +2_1_ПX\а_пК ,k_mj ,

Е° =

*-о

/V                    z п 4s ц, (0) + л^Спап sh(апЛ j ,

Е° =2W^X^A₃S

^ Qvk^kf sin^₇ +л£с^а„¹ sh(а„Л ¹) .

Используя метод редукции, сведём решение бесконечной системы алгебраических уравнений (17) к решению системы линейных алгебраических уравнений следующего вида:

w_mk>yw^=p_m, т = 0Д,2,...,М.                 (18)

7=0

После определения коэффициентов wm Qn = 0Д,...,М^ для фиксированного значения М из (18) находим контактные напряжения м qUA^^wq 0<г<1,                  (19)

m=0

и прогибы пластины

м

^WV>=lL^Wm4>_mV>' 0<Г<1.                     (20)

/77=0

Полученные формулы могут быть использованы для расчёта характеристик контактного взаимодействия многослойной пластины с основанием сложной структуры в зависимости от граничных условий и характера нагрузки на пластину. Так как неоднородность пластины и многослой-ность в рамках рассмотренной модели влияет только на величину цилиндрической жёсткости D, будем считать, что увеличение количества слоёв в пластине влияет на значение параметра D и, соответственно, на значение параметра s.

Рассмотрим случай влияния на распределение контактных напряжений под пластиной равномерно распределённой нагрузки. В случае, когда края пластинки не закреплены по периметру, при вычислении контактных напряжений использовался результат работы [16]. Для закреплённых краёв использовалась формула (19).

Пусть пластина лежит на мягком покрытии (₽ = 100), модуль Юнга которого меняется по закону:

Е1(г) = Е0.ф(г), ф(г) = ф0+(ф0-1).г.

Показатель неоднородности ф0 = const > 1 характеризует отношение модуля Юнга на поверхности покрытия (z = 0) к модулю Юнга подложки. Ограничимся рассмотрением случая ф0 = 3,5, что соответствует сочетанию мягкого (алюминий, серебро, медь, свинец и т. д.) и жёсткого (железо, сталь, палладий, молибден и т. д.) металлов.

При численной реализации было выявлено, что граничные условия для жёстких пластин практически не оказывают влияние на распределение контактных напряжений. Причём диапазоны параметров, для которых это справедливо, следующие: для А = 4 — s < 0,1, для А = 0,05 — s < 0,07.

На рис. 1, 2 построены графики контактных напряжений в случае гибких пластин для указанного выше закона изменения модуля Юнга с глубиной. Из графиков видно, что условия закрепления краёв пластины оказывают влияние на распределение контактных напряжений под пластиной.

Заключение. Получено приближённое аналитическое решение задачи об изгибе круглой многослойной пластины постоянной толщины, лежащей на упругом неоднородном основании сложной структуры.

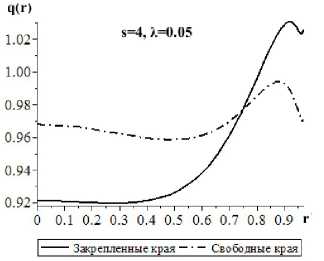
Рис. 1. Распределение контактных напряжений под гибкой (s = 4) пластиной при большой зоне контакта относительно толщины покрытия

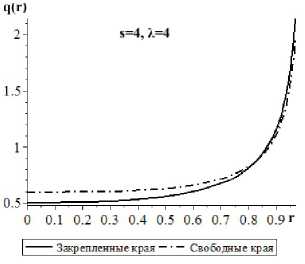
Рис. 2. Распределение контактных напряжений под гибкой пластиной при малой зоне контакта относительно толщины покрытия

Построенная математическая модель эффективна в широком диапазоне значений как геометрического (Л), так и физических (s, Р) параметров задачи и может быть использована для расчётов неоднородных пластин Кирхгофа при различных граничных условиях на краю пластинки. Библиографический список

• 1.    Hager, А. М. Short-Fibre Reinforced, High-Temperature Resistant Polymers for a Wide Field of Tribological Applications / A. M. Hager, M. Davies // Advances in Composite Tribology / K. Friedrich, ed. — Amsterdam : Elsevier, 1993. — Pp. 107-157.

• 2.    Friedrich, K. Wear of polymer composites / K. Friedrich, R. Reinicke, Z. Zhang // Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology. — 2002. — Vol. 216, iss. 6. — Pp. 415^426.

• 3.    Моделирование фрикционного взаимодействия композиционных покрытий триботехнического назначения / И. Г. Горячева [и др.] //Трение и износ. — 2012. — Т. 33, № 6. — С 557-565

• 4.    Васильев, А. С. Кручение упругого полупространства с многослойным покрытием периодической структуры / А. С. Васильев, Е. В. Садырин, М. Е. Васильева // Вестник Дон. гос. техн, ун-та. - 2013. - № 5/6 (74). - С. 6-13.

• 5.    Горбунов-Посадов, М. И. Расчёт балок и плит на упругом полупространстве // Прикладная математика и механика. — 1940. — Т. 4, вып. 3. — С. 61-80.

• 6.    Ишкова, А. Г. Об изгибе полосы и круглой пластины, лежащих на упругом полупространстве // Инженерный сборник. — 1960. — Т. 23. — С. 171-181.

• 7.    Гребенщиков, В. Н. Расчёт круглой пластинки на упругом полупространстве // Теория расчёта и надёжность приборов : сб. тр. II Саратовской обл. конф, молодых учёных. — 1969. — С. 48-51.

• 8.    Александров, В. М. Универсальная программа расчёта изгиба балочных плит на линейно-деформируемом основании / В. М. Александров, Л. С. Шацких // Труды 7-й Всесоюзной конференции по теории оболочек и пластин. — Москва, 1970. — С. 46-51.

• 9.    Шацких, Л. С. К расчёту изгиба плиты на упругом слое // Известия Академии наук СССР. Механика твёрдого тела. — 1972. — № 2. — С. 170-176.

• 10.    Александров, В. М. Эффективное решение задачи о цилиндрическом изгибе пластинки конечной ширины на упругом полупространстве / В. М. Александров, И. И. Ворович, М. Д. Солодовник // Известия Академии наук СССР. Механика твёрдого тела. — 1973. — № 4. — С. 129-138.

• 12.    Босаков, С. В. К решению контактной задачи для круглой пластинки / С. В. Босаков // Прикладная математика и механика. — 2008. — Т. 72, № 1. — С. 59-61.

• 13.    Kashtalyan, М. Effect of a functionally graded interlayer on three-dimensional elastic deformation of coated plates subjected to transverse loading / M. Kashtalyan, M. Menshykova // Composite Structures. — 2009. — Vol. 89, № 2. — Pp. 167-176.

• 14.    Kashtalyan, M. Three-dimensional elasticity solution for bending of functionally graded rectangular plates / M. Kashtalyan // European Journal of Mechanics A/Solids. — 2004. — Vol. 23, № 5. — Pp. 853-864.

• 15.    Silva, A. R. D. Numerical methods for analysis of plates on tensionless elastic foundations / A. R. D. Silva, R. A. M. Silveira, P. B. GoncBalves // International Journal of Solids and Structures. — 2001. — Vol. 38, № 10-13. — Pp. 2083-2100.

• 16.    Митрин, Б. И. Распределение контактных напряжений под круглой пластиной, лежащей на мягком слое / Б. И. Митрин, С. С. Волков // Вестник Дон. гос. техн, ун-та. — 2013. — № 5/6 (74). - С. 14-25.

• 17.    Айзикович, С. М. Асимптотическое решение одного класса парных уравнений / С. М. Айзикович // Прикладная математика и механика. — 1990. — Т. 54, вып. 5. — С. 872-877.

• 18.    Лурье, А. И. Теория упругости / А. И. Лурье. — Москва : Наука, 1970. — 824 с.

• 19.    Белубекян, М. В. К вопросу колебаний неоднородной по толщине пластинки / М. В. Бе-лубекян // Известия национальной академии наук Армении. Механика. — 2002. — Т. 55, № 3. — С. ЗИ 41.

• 20.    Цейтлин, А. И. Об изгибе круглой плиты, лежащей на линейно деформируемом основании / А. И. Цейтлин // Известия АН СССР. Механика твёрдого тела. — 1969. — № 1. — С. 99-112.

• 21.    Айзикович, С. М. Осесимметрическая задача о вдавливании круглого штампа в упругое, неоднородное по глубине полупространство / С. М. Айзикович, В. М. Александров // Известия АН СССР. Механика твёрдого тела. — 1984. — Т. 19, № 2. — С. 73-82.

• 22.    Айзикович, С. М. Асимптотическое решение задачи о взаимодействии пластины с неоднородным по глубине основанием / С. М. Айзикович // Прикладная математика и механика. — 1995. - Т. 59, вып. 4. - С. 688-697.

И. Александров, В. М. Асимптотическое решение задачи о цилиндрическом изгибе пластинки конечной ширины на упругом полупространстве / В. М. Александров, М. Д. Солодовник // Прикладная механика. — 1974. — Т. 10, вып. 7. — С. 77-83.

Материал поступил в редакцию 12.03.2014.