Осмотическое напряжение в трехмерном коллоидном кристалле в модели уравнения Пуассона-Больцмана

описывается моделью постоянной плотности заряда. При этом используется приближение большой диэлектрической проницаемости электролита по сравнению с диэлектрической проница- емостью материала частиц, что типично для водных растворов. В этом случае электрический потенциал в области электролита оказывается независимым от потенциала внутри частицы.

Электростатический потенциал ф в области электролита описывается нелинейным дифференциальным уравнением Пуассона-Больцмана [8, 9]. Все макроскопические свойства коллоидного кристалла, обусловленные электростатическим взаимодействием его частиц, выводятся из решений уравнения Пуассона-Больцмана и со- ответствующего ему тензора напряжений П.. В данной работе вычисляется тензор осмотическо- го напряжения Tij

в кристалле в состоянии по- коя при отсутствии деформации. Для снижения затрат вычислительных ресурсов производится учет симметрии кристалла, что позволяет уменьшить ее области определения при численном решении. Предлагаемый подход может быть распространен также на решение задач при наложении деформации.

В общем случае уравнением Пуассона-Больцмана для электрического потенциала ф в области электролита, имеет вид [8, 9]

V 2 ф =-- — £ z.Q e n 0, exp ( - z^j kT ⁾ , (1)

E0E i

где E0 - электрическая постоянная, E - диэлектрическая проницаемость электролита, qe – элементарный заряд, zi – валентность i -ой компоненты электролита, n0i – объемная концентрация i -ой компоненты электролита в объеме, то есть в области вдали от заряженных частиц, где потенциал принимается равным нулю, k – постоянная Больцмана, T – абсолютная температура. Суммирование в (1) осуществляется по всем компонентам электролита. В дальнейшем рассматривается случай бинарного симметричного одновалентного электролита, или 1:1 электролита, для которого уравнение Пуассона-Больцмана является хорошим приближением. Таким образом, электролит имеет две компоненты с валентностями z^ = +1 и z 2 = —1, при этом n01 = n02 = n0 .

Для приведения уравнения и всех последующих выражений к безразмерному виду вводятся следующие величины: длина Дебая для 1:1 элект-

• _— 1 2 — 1/2

ролита К = ( 2 n 0 qe ] E₀EkT 1 для измерения длины и величина kT qe для измерения электрического потенциала. В этих единицах уравнение Пуассона-Больцмана для исследуемой системы записывается в следующей безразмерной форме:

V ² ф = sh ф .            (2)

Осмотическое напряжение T ij вычисляется с помощью фундаментального тензора напряжений П , следующим образом [10]:

T = V X r m ¹ [ П/ а , m ^. c               s ⁽ m )

Здесь V c - объем элементарной ячейки, r ( m ¹ – вектор решетки Бравэ, разделяющий эквивалентные точки каждой пары m противолежащих граней ячейки, а интегрирование осуществляется по одной (любой) из двух граней в каждой паре. Нормали на всех внешних гранях направлены наружу. Тензор П , описывает локальное напряжение в системе, электрический потенциал которой подчиняется дифференциальному уравнению Пуассона-Больцмана. В безразмерной форме для бинарного симметричного одновалентного электролита он имеет вид

П = Vф®Vф — (| |v ф ² + ch ф — 1) I , (4) где ф = ф ( r ) - электрический потенциал, I -единичный тензор.

В силу высокой симметрии о. ц. к. решетки, тензор осмотического напряжения в кристалле с такой решеткой имеет вид Tj = — p3j, где 3у -символ Кронекера, а p – обычное осмотическое давление. Таким образом, полный тензор осмотического напряжения определяется всего одним параметром p , и для его полного определения достаточно вычислить любую из трех диагональных компонент.

Для вычисления осмотического напряжения согласно (3) в качестве элементарной ячейки удобно использовать ячейку Вигнера-Зейтца кристалла. Прежде всего, это связано с ее высокой симметрией. Последовательное использование соображений симметрии позволяет существенно сократить геометрическую область определения задачи. Кроме того, грани ячейки Вигнера-Зейтца являются одновременно плоскостями зеркальной симметрии кристалла. Это обстоятельство позволяет избежать наложения периодических граничных условий, требуемых в общем случае [10], и использовать на этих гранях простейшие однородные граничные условия Неймана, что также выгодно с вычислительной точки зрения.

Элементарная ячейка Вигнера-Зейтца о. ц. к. решетки представляет собой усеченный октаэдр. Она имеет 7 пар противолежащих граней. Пусть a – параметр условной кубической ячейки для о. ц. к. решетки, рассматриваемая частица находится в начале координат прямоугольной декартовой системы координат x , y , z , а запись векторов осуществляется в координатном базисе этой системы координат. Векторы решетки Бравэ r ( m ¹ для о. ц. к. решетки, используемые в (3) для вычисления осмотического напряжения, приведены в табл. 1.

Учет симметрии кристаллической решетки позволяет ограничиться при численном решении областью меньшего объема, чем имеет ячейка Вигнера-Зейтца. Редуцированная область получается из полной ячейки Вигнера-Зейтца рассечением плоскостями (100), (010), (001) и (110), (101),(011), проходящими через центр частицы. Эти плоскости также являются плоскостями зеркальной симметрии кристалла, что предполагает выполнимость на них однородных граничных условий Неймана.

Таким образом, определение электрического потенциала ф сводится к решению краевой задачи для уравнения Пуассона-Больцмана (2) на указанной области. При этом на всех плоских границах в силу симметрии выполняется однородное граничное условие Неймана вида

—V ф ■ n = 0 , (5) где n – вектор внешней нормали. На поверхности частицы граничные условия определяются

Таблица 1. Векторы, разделяющие пары противолежащих граней в о. ц. к. решетке

m	1	2	3	4	5	6	7
( m 1 r , в ед. a	( 1,0,0 )	( 0,1,0 )	( 0,1,0 )	( 121 ) ( 2 2 2 )	/ 1 1 1 / 1 2, 2,2 )	/ 1 1 1 / 1 2,2, 2 )	/ 1 1 1 / ( 2, 2, 2 )

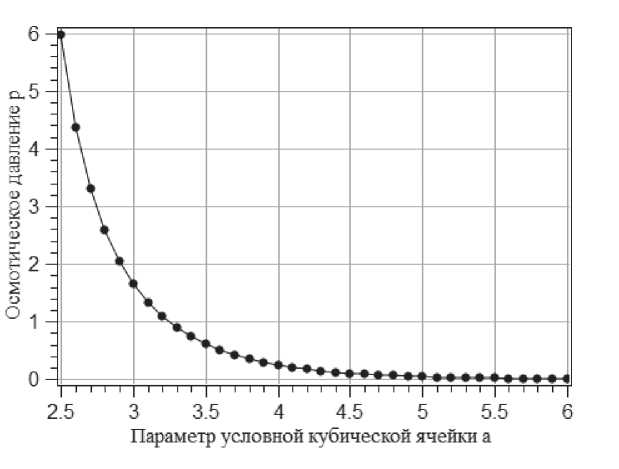
Рис. 1. Осмотическое давление коллоидного кристалла с о. ц. к. решеткой

поверхностной плотностью заряда г на ней и сводятся к неоднородным граничным условиям фон Неймана вида

-V^- n = Г. (6)

Граничные условия (6) отражает выполнение приближения большой диэлектрической проницаемости. Для вычисления тензора T ij интегрирование согласно (3) с учетом (4) выполняется по фрагментам поверхности ячейки Вигнера-Зейтца, находящимся в области определения задачи. Полные интегралы восстанавливаются по симметрии.

Численное решение краевой задачи и определение осмотического напряжения проводилось при фиксированных параметрах г = 2 и R = 1 для значений параметра a в диапазоне от 2,5 до 6,0. Решение осуществлялось методом конечных элементов с использованием градиентных нерегулярных сеток тетраэдральных элементов. Компьютерная программа написана на языке программирования C++ с использованием библиотеки libMesh [11]. Работа выполнена с использованием ресурсов суперкомпьютерного комплекса МГУ имени М.В. Ломоносова [12] Результаты вычислений показаны на рисунке 1.

Анализ данных на рисунке 1 показывает, что осмотическое давление изменяется монотонно во всем диапазоне исследованных значений параметра условной кубической ячейки. При увеличении плотности давление резко нарастает. В соответствии с тем, что на поверхности частиц заряд неизменен, ожидается, что осмотическое давление стремится к бесконечности при приближении частиц к контакту.

Предложенная математическая модель может быть использована как основа для проведения вычислительных экспериментов по определению упругих постоянных коллоидного кристалла. В этом случае тензор осмотического напряжения должен вычисляться не только для исходного со- стояния покоя, но и для кристалла в условиях деформации. При этом в модель должна быть изменена и дополнена в ряде аспектов. Прежде всего, поскольку симметрия кристалла, вообще говоря, понижается при деформации, область определения задачи должна быть увеличена. Точная пространственная область кристалла, которая может быть выбрана в качестве области определения, зависит от типа деформации. Однако, эту область по-прежнему можно выбрать так, что ее внешние границы будут плоскостями зеркальной симметрии кристалла, а, значит, на них будут выполняться однородные граничные условия Неймана. Векторы r(m), разделяющие пары противоположных граней, подлежат преобразованию, определяемому типом деформации. Так- же возрастет число независимых компонент тен- зора Tij , подлежащих определению.