Основные и сопряженные уравнения переноса и задачи оптимизации
Автор: Мурадов Ф.А., Набиева С.С.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Основной раздел
Статья в выпуске: 7 (25), 2017 года.
Бесплатный доступ
В статье рассмотрена процесс распространения промышленных выбросов в атмосфере происходит за счет адвективного их переноса воздушными массами и диффузии, обусловленной турбулентными пульсациями воздуха. Осредненный поток субстанций, переносимых воздушными массами, имеет адвективную и конвективную составляющие, а осредненные флуктуационные их движения можно интерпретировать как диффузию на фоне основного осредненного движения, связанного с ним.
Математическая модель, перенос и диффузия вредных веществ, гидромеханика, численный алгоритм
Короткий адрес: https://sciup.org/140272095
IDR: 140272095
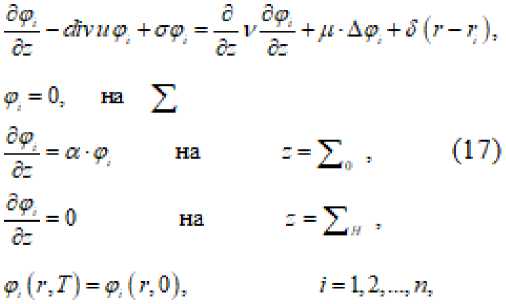
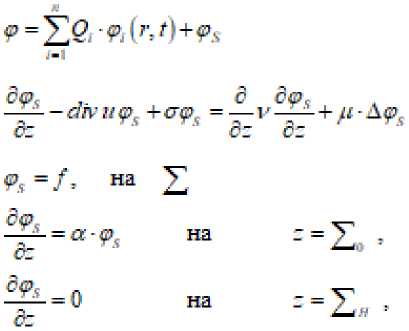
Список литературы Основные и сопряженные уравнения переноса и задачи оптимизации
- Ravshanov N., Sharipov D., Muradov F. Computational experiment for forecasting and monitoring the environmental condition of industrial regions // Theoretical & Applied Science: International Scientific Journal. - 2016. - Vol. 35. - Issue 3. - Pp. 132-139. - DOI: 10.15863/TAS.2016.03.35.22
- Копченова Н.В., Марон И. А. Вычислителная математика в примерах и задачах. - М.: Наука, 2008. - 368 с.
- Равшанов Н., Шарипов Д.К., Ахмедов Д. Моделирования процесса загрязнения окружающей среды с учетом рельефа местности погодно-климатических факторов // Информационные технологии моделирования и управления - Воронеж, 2015.№3. - С. 222-235.
- Фаддеева В.Н. Метод прямых в применении к некоторым краевым задачам//Труды Математического института АН СССР им. В.А. Стеклова, т. XXVIII (28), М., 1949.
