Основные компоненты организации самостоятельных работ студентов по предмету начертательная геометрия

Уровень профессиональной подготовки будущих специалистов, в частности конструкторов-дизайнеров в системе высшего технического образования, прямо связано освоением основных фундаментальных технических дисциплин.

Техническое, конструкторское и творческое знание и умение у студентов наполняется и формируется изучением таких фундаментальных технических дисциплин, как «Начертательная геометрия и перспектива изображения».

Основная задача и цель курса «Начертательной геометрии» – формирование у студентов качества мышления, студенты должны самостоятельно осмыслить расположение объектов в пространстве или поверхности. Студент должен мысленно создать себе объемное представление об изделии или конструкции дизайнерского или другого технического проекта, должен развивать интеллектуальный уровень, вникать в технические чертежи узлов, механизмов.

Учитывая, что «Начертательная геометрия» фундаментальная наука о технике, мы видим, что в последние годы геометро-графическая подготовка в технических вузах непрерывно развивается и преодолевает новые этапы.

Благодаря непрерывным усиленным работам многих ученых-преподавателей в начертательной геометрии разработан новый уровень овладения знаниями – трехмерное геометрическое моделирование построение чертежей. Оно реализуется во всех современных пакетах САПР и внедрены в образовательный процесс [2].

Учитывая, что изучение и построение предмета на 3D геометрическое моделирование – это современное требование подготовки профессиональных специалистов и оно открыло новые возможности решение задач в начертательной геометрии.

В связи с переходом на новый стандарт 4-го поколения, резко снизились аудиторные часы по начертательной геометрии. Но, несмотря на все эти и другие трудности ученые-преподаватели успешно решают все проблемы преподавания начертательной геометрии.

Известно, что по курсу начертательной геометрии полностью осваивать запланированную программу по дисциплине представляется достаточно трудоемким. Порядка 60% от общей трудоемкости дисциплины по календарно-тематическому плану отводится на самостоятельное изучение студентами. Наглядность раздаточного материала хороша на начальном этапе графического обучения, однако, появляется необходимость разработки такого ресурса, который сконцентрировал бы в себе краткое изложение теоретического содержания, необходимый объем практических работ был бы многовариантен, направлен на развитие творческого интереса учащихся, способствовал бы самовыражению, самореализации, быстрому и полному освоению учебного материала. Следовательно, усилия ученых-педагогов должны быть направлены для активизации самостоятельных работ у студентов.

Самостоятельная учебная работа по начертательной геометрии у будущих профессионалов преследуется профессиональной компетенцией. Профессиональная компетенция предполагает глубоко развитые способности познавательной самостоятельности, которая в свою очередь, не может быть достигнута без проявления волевых усилий со стороны обучаемого. В укреплении воли важную роль играет мотивация, которая во многом будет сформирована теми отношениями, которые сложились в обществе. Самостоятельная учебная работа студентов по начертательной геометрии – процесс личностный и требует мысленно осмысливать те или иные задачи, и успешно достигает к цели только в условиях сознательной активности личности [6].

На эффективность самостоятельных работ у студентов по начертательной геометрии влияет интеллектуально познавательный компонент, и она рассматриваются через способности студента и рефлексии. Интеллектуально познавательные компоненты у студентов во многом зависят от уровня изначальных знаний студента и способностей.

Процесс активизации самостоятельных работ у студентов достигается определенными педагогическими условиями и педагогическими техниками.

Первое педагогическое условие это – высокий уровень профессиональной компетентности преподавателя. При самостоятельной учебной работе у преподавателя роль руководителя не снижается, а наоборот, еще больше возрастает; второе условие – коллективное общение. Развитие коллективных форм учебно-познавательной деятельности воздействует на решение сложных задач по начертательной геометрии, а так же, во время освоения компьютерных программ в моделировании сложных геометрических фигур и расположение их на разных поверхностях [2].

Действительно, активность и сознательность в обучении не образуется сами по себе. Для развития активности требуется применение преподавателям определенных методов обучения, приемов и дидактических средств и т.д. Преподаватели начертательной геометрии в университете решают множество задач, среди них наиболее значительными являются рациональное планирование занятий и поиск средств и условий мотивации, развития волевых усилий студента; раскрытие и развитие способностей к познавательной самостоятельности, контроль результативности процесса обучения [3].

Формирование профессиональной компетенции у студентов в процессе активизации самостоятельных работ дополняется применением новых обучающих технологий, использование которых предполагает компьютеризацию и обеспечение программ продуктов учебного процесса. Практика показывает, что использование компьютерных технологий в образовательном процессе повышает информативность, интенсивность и результативность.

Выполнение чертежей по компьютерной технологии намного отличается от чертежей, выполненных от рук. Современные методы и технологии автоматизированного проектирования компьютерной технологией и решение задач в контрольных работах по курсу начертательной геометрии успешно используется на самостоятельных работах студента на кафедре «Начертательной геометрии и графического дизайна» Ошского технологического университета имени акад. М.М. Адышева.

В целях формирования навыков у студентов самостоятельной продуктивной работы сотрудниками кафедры разработаны методические указания к выполнению контрольных работ по курсу “Начертательная геометрия”, которые включают более 12 заданий. Применение информационных технологий способствует успешной организации самостоятельной работы студентов, облегчает внеаудиторную работу, а также позволяет многократно усилить индивидуальный подход в обучении студентов разного уровня подготовки и имеющихся у них способностей.

В учебном процессе университета внедряется сенсорная доска , разработанная сотрудниками факультета кибернетики и информационных технологий, во главе профессора Ш. А. Сайдаматова. Разработанная интерактивная сенсорная доска имеет модульную конструкцию и очень удобна в эксплуатации (рис.1).

Рисунок 1. Общий вид сенсорной доски

Программное обеспечение доски позволяет обучать одновременно до 10 пользователей, которые могут делать надписи и вносить комментарии поверх рабочих страниц доски, видео и других приложений.

Рассмотрим примеры решения 2-3 задачи контрольной работы №1 непосредственно на сенсорном экране. Для этой цели используется программа AutoCad.

Согласно условиям второй задачи требуется определить расстояние от точки D до плоскости треугольника АВС.

На третьей задаче требуется определить углы наклона перпендикуляра, опущенного из данной точки D на данную плоскость треугольника АВС, к плоскостям проекций.

Координаты точек заданы индивидуально по вариантам. Задача выполняется в следующем порядке:

• а)    Сначала запустим программу AutoCad, с помощью кнопки «отрезок» построим эпюру по заданным координатам точек А, В, С и D плоскости треугольника α(∆АВС) по оси Х. С помощью команды «многоугольник» и «выдавить» построим эпюру плоскости.

• б)    для построения перпендикуляра из точки к плоскости используем перпендикулярность прямой и плоскости. Перпендикуляр к плоскости это прямая, проведенная перпендикулярно к любым двум пересекающимся прямым, лежащим в плоскости. Для облегчения графических построений мы за этих прямых берем горизонталь и фронтальные плоскости. В нашем случае поступаем так: Через точку А проведем фронтальную линию А₂(А₂, А₂) и горизонталь А₁(А₁, А₁).

• в)    горизонтальная проекция искомого перпендикуляра проходит через D₁ перпендикулярно к А₁, а фронтальная – через D₂ перпендикулярно к А₂.

• г)    основание перпендикуляра определяется как точка пересечения этого перпендикуляра с плоскостью. Заключаем его в горизонтально – проецирующую плоскость β (задаем ее следом h_o β).

• д)    находим линию пересечения плоскости с плоскостью треугольника α(АВС) – прямую M_N(M_N, M_N). Получаем точку К₂ – фронтальную проекцию основания перпендикуляра – и по К₂ находим К₁. В результате получаем проекции перпендикуляра DК (D_К, D_K), опущенного из точки D к плоскости α(∆АВС).

• е)    для того, чтобы определить расстояния от точки D до плоскости треугольника α(АВС) используем метод прямоугольного треугольника, Натуральная величина перпендикуляра D_К может быть определена как величина гипотенузы прямоугольного треугольника, одним катетом которого является проекция отрезка (D_К, D_К) на какой – либо плоскости проекций, а другим – разность расстояний концов (y или z) отрезка до этой плоскости.

На рисунке 2 построен прямоугольный треугольник DКD*. В этом треугольнике катет DD* равен разности расстояний точек DК до горизонтальной плоскости проекций (DD*= ∆z), АD. К является натуральной величины.

Таким образом, особенность сенсорной доски в том что, соединив через процессор компьютера или ноутбука запустив программы, можно решать задачи прямо на экране с пальцами рук или жестом. Это дает возможность боле удобно и легко работать с инструментами и начертить с пальцами рук на экране. Еще одно преимущество сенсорной доски в том что, в одном экране можно создавать от

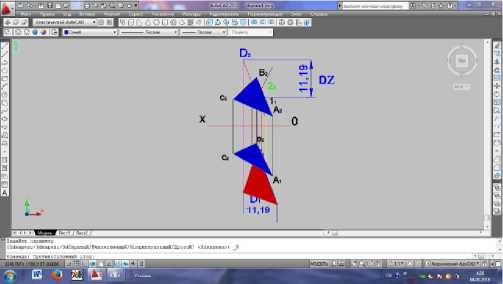
Рисунок 2. 3D вид построенной натуральной величины D*

одного до четырех или больше рабочих столов, которые позволяют работать в одном сенсорном экране несколько студентов.

Наша практика показала, что в одной интерактивной сенсорной доске целесообразно могут одновременно заниматься самостоятельными работами по начертательной геометрии больше четырех, максимум до шести студентов. С появлением больше шести студентов в аудитории начинается вмешательство друг друга при выполнении задачи. Если больше шести студентов в аудитории то, их нужно разделить по мини группам.

Основное преимущество выполнения задач в сенсорном экране – дает студенту возможность свободно двигаться в аудитории и широко осмысливать. На собеседованиях со студентами было выявлено, что в большинстве занятий студенты проводят время сидя на аудиторных скамейках, от которых наблюдается физическая и физиологическая усталость. А при решении задач по начертательной геометрии, двигаясь на стойке, на сенсорном экране они чувствует себя в обычном свободном режиме.

Таким образом, на основании вышеизложенного можно сделать следующие выводы:

– выявлено, что использование интерактивного метода обучения с помощью сенсорной доски способствует формированию эмоционально-волевых качеств студентов при решении задач по начертательной геометрии, а также развивают творческие способности и обеспечивает креативный подход при выполнении расчетно-графических работ.

– проведенные занятия показали эффективность моделирования геометрических фигур на сенсорном экране, позволили в значительной степени развивать интеллектуальнопознавательные способности студентов.