Основы модели квазиоптимальных приближений изображения
Автор: Харинов Михаил Вячеславович
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Информационные системы и технологии
Статья в выпуске: 1, 2016 года.
Бесплатный доступ
В статье обобщаются результаты исследований, представленных в серии предыдущих публикаций по, так называемой, «проблеме сегментации» или автоматического выделения объектов на изображении. Для компьютерного выделения объектов формулируется постановка задачи и предлагается модель сегментации цифрового изображения. Перечисляются основные положения модели. Приводятся результаты очередного эксперимента и обсуждаются особенности организации скоростных вычислений в ограниченном объеме оперативной памяти компьютера.
Сегментация, кусочно-постоянное приближение, суммарная квадратичная ошибка, минимизация, обратимые вычисления
Короткий адрес: https://sciup.org/14835168
IDR: 14835168 | УДК: 004.932 | DOI: 10.18101/2304-5728-2016-1-60-72
Текст научной статьи Основы модели квазиоптимальных приближений изображения
При современных темпах внедрения технологий искусственного интеллекта (ИИ) в ближайшие годы следует ожидать появления эффективных средств создания продуктов ИИ благодаря унификации прикладных решений. Указанная цель декларируется в проекте PPAML (Probabilistic Programming for Advancing Machine Learning) американского агентства DARPA (Defense Advanced Research Projects Agency), который начат в 2013 и закончится в 2017 г.1 В результате планируется разработать программные средства, поддерживающие эффективное создание приложений ИИ силами рядовых инженеров-программистов.
В области машинного зрения для автоматизации распознавания лиц, искусственных и природных объектов на дистанционных изображениях, оценки расстояний по стереоснимкам, а также в многочисленных других типовых задачах обработки изображений цель сводится к созданию программного средства, помогающего неискушенному в обработке изображений программисту выделять для дальнейшего распознавания «объекты интереса» среди многих объектов, детектируемых на изображении компьютером. При этом программисту необходимо понимать и представлять результаты предварительной обработки изображения в наглядной модели.
В наглядной модели изображение и объекты описываются в матричной (табличной) форме. Подобная модель необходима для первоначального анализа и упорядочения визуальных данных так, чтобы программист без особых усилий представлял, какие объекты «видит» компьютер на изображении и в терминах этих объектов программировал выделение и распознавание целевых объектов сцены посредством измерения и запоминания характерных признаков объектов, фильтрации объектов по заданным признакам и др. стандартных приемов обработки.
Однако, вычисления с объектами, заданными заранее не установленными множествами пикселей, без специальных приемов оптимизации требуют чрезмерно много памяти и времени обработки. Поэтому для практической реализации наглядной модели оказывается необходимым разработать эквивалентную модель вычислений в терминах структуры данных, поддерживающей скоростную обработку изображения в ограниченном объеме оперативной памяти компьютера. Подходящая структура данных на основе динамических деревьев Слейтора-Тарьяна [1] в приложении к адаптивной иерархической сегментации изображений была предложена в СПИИРАН в начале 90-х годов прошлого столетия [2] и в настоящее время начала эксплуатироваться также за рубежом [3].
Развитие аппарата адаптивной иерархической сегментации [2,4,5] в сочетании с активно развиваемыми в США методами сегментации изображения посредством оптимальных кусочно-постоянных приближений [6, 7] и обратимых вычислений [8] привело к созданию модели иерархической квазиоптимальной сегментации [9–12], обсуждаемой в статье.
объектов достигается вычислением не одного или нескольких приближений изображения, а аппроксимацией всей последовательности оптимальных приближений иерархической последовательностью квазиоптималь-ных приближений (рис.1).

Рис. 1. Задача аппроксимации оптимальных приближений квазиопти-мальными приближениями
На рис. 1 для последовательностей приближений изображения показаны графики суммарной квадратичной ошибки аппроксимации изображения E в зависимости от числа кластеров g , изменяющегося от 1 до N . Нижняя серая жирная кривая, отвечает оптимальным приближениям. Верхние кривые отвечают вариантам последовательности квазиоптималь-ных приближений.
Последовательность оптимальных приближений изображения, вообще говоря, не является иерархической. Поэтому последовательность квазиоп-тимальных приближений вычисляется не однозначно. Поскольку последовательность оптимальных приближений описывается выпуклой кривой, в модели полагается, что квазиоптимальные приближения также должны описываться выпуклыми кривыми (рис. 1).
Из рис. 1 следует, что в модели квазиоптимальных приближений не всякое разбиение изображения может являться результатом сегментации. Например, изображение из не всех одинаковых пикселей не может разделиться на пару совпадающих по средней яркости частей, так как условие выпуклости тогда нарушится. Характерно, что для итеративных алгоритмов сегментации выпуклая зависимость E от g , как правило, нарушается при числе сегментов в начальном диапазоне, приблизительно, от 1 до 100, и при некотором числе сегментов достигается точка перегиба, которую в алгоритмах слияния часто используют для останова процесса итеративной сегментации с целью нахождения кусочно-постоянного приближения изображения с выделенными «объектами интереса» [14]. В обсуждаемой модели объекты задаются полными иерархическими последовательностями приближений с числом кластеров 1 до N и все являются целевыми. При этом нарушений выпуклости последовательности значений E не допускается, что способствует снижению ошибки аппроксимации E и устойчивому выделению объектов при модификации содержания изображения [11].
2. Модель квазиоптимальной иерархической сегментации цифрового изображения
На сегодняшний день, модель выражается следующими пятью основными положениями.
Положение 1. Изображение состоит из изображений, которые задаются кусочно-постоянными приближениями и именуются «объектами».
Положение 2. Объекты составляют бинарную иерархию.
Положение 3. Результирующая последовательность квазиоптималь-ных приближений изображения с различным числом кластеров описывается выпуклой зависимостью суммарной квадратичной ошибки.
Положение 4. Любая иерархическая последовательность приближений изображения по определенному алгоритму преобразуется в последовательность приближений, описываемых выпуклой последовательностью значений суммарной квадратичной ошибки E или среднеквадратичного отклонения σ приближения от изображения.
Положение 5. Последовательность квазиоптимальных приближений представима в виде изображения, называемого «инвариантным представлением».
В первом положении утверждается, что изображение структурировано и рассматривается как множество, состоящее из элементов одной природы, которые обрабатываются по единым алгоритмам. При этом термины «изображение», «объект», «кластер пикселей», в частности, «сегмент изображения», употребляются как синонимы. Термин «объект» преимущественно используется при рассмотрении одного изображения как элемента другого изображения.
Благодаря второму положению в вычислениях удается обойти NP -трудную задачу получения оптимальных приближений изображения, которая заменяется полиномиально сложной задачей аппроксимации неиерархической последовательности оптимальных приближений посредством иерархической последовательности квазиоптимальных приближений изображения.
Третье положение устанавливает закон, согласно которому квазиопти-мальные приближения изображения сохраняют аналогичное свойство оптимальных приближений. При этом для множества получаемых кластеров необходимо, чтобы любая тройка вложенных друг в друга объектов описывалась выпуклой последовательностью значений суммарной квадратичной ошибки.
Согласно четвертому положению любая иерархическая последовательность приближений преобразуется в последовательность квазиопти-мальных приближений изображения, которые :
- ограничены по числу сегментов;
- близки к изображению по суммарной квадратичной ошибке;
- в зависимости от числа кластеров g описываются выпуклой последовательностью значений Eg суммарной квадратичной ошибки:
3. Применение обратимого слияния кластеров для минимизации ошибки аппроксимации
E g < E g - 1 2 E g + 1 , g = 2,3,..., N - 1.
Согласно пятому положению любую иерархическую последовательность приближений можно задать как новое изображение, которое называется «инвариантным представлением», так как не меняется при определенной модификации исходного изображения [4,9]. Таким образом, изображение описывается семейством переплетающихся выпуклых кривых рис. 1 и массивом инвариантных представлений, порождающих инвариантное пространство , которое отличается от традиционного признакового пространства тем, что в качестве признака учитывает единственную среднюю яркость по-разному усредняемых пикселей и не меняется при масштабировании изображения посредством дублирования пикселей, а также при линейной модификации яркостей пикселей изображения.
В программной реализации практический смысл модели квазиопти-мальной иерархической сегментации состоит в том, что для изображения, скажем, из 1 млн. пикселей программист получает 1 млн. квазиоптималь-ных приближений и 1 млн.999 тыс. 999 вложенных изображений объектов, которые машина строит «сама». При этом квазиоптимальные приближения лучше оптимальных тем, что составляют иерархическую последовательность и поэтому в кодированном виде удерживаются в RAM, быстро строятся, преобразуются, а также оказываются гораздо эффективней для оперативного анализа признаков объектов и выполнения другой обработки. Неоднозначность аппроксимации оптимальных приближений квазиоптимальными отражает двойственную неоднозначность объектов, детектируемых в контексте решения различных прикладных задач. При этом каждый объект определяется выбором иерархической последовательности приближений и номером вложения в большие объекты. Каждая иерархическая последовательность приближений кодируется как изображение (инвариантное представление), и исходная картинка независимо от масштабирования и линейного изменения яркости преобразуется в несколько инвариантных картинок, которые обеспечивают устойчивое выделение объектов посредством аппарата признаковых пространств [13].
Генерация иерархической последовательности квазиоптимальных приближений, выполняется в алгоритмах слияния/разделения кластеров пик- селей, в частности, сегментов изображения из условия минимизации суммарной квадратичной ошибки.
В вычислениях поддерживается обратимая операция слияния кластеров, при которой для каждого кластера 1 автоматически запоминается пара кластеров 2, 3 , слиянием которых он получен. В этом случае, аналитическое обоснование модели выражается несколькими элементарными формулами для приращения суммарной квадратичной ошибки ΔE при трех базовых операциях с кластерами пикселей 1, 2, 3 из n 1, n 2 , n 3 пикселей со значениями I 1, I 2 , I 3 трехмерных средних яркостей по цветовым компонентам изображения [5, 9–12]:
1. Слияние ( merge ): ΔEmerge
W i - 1 2« 2 ^ o ; n1 + n 2
-
2. Разделение ( divide ): AE divide (1) = - AE merge ( 2, 3) < 0 ;
-
3. Коррекция ( correct ):
AEcorrect = ^ Цз - 12 |I - '^ Цз - IЦ, n 2 + n 3 n 1 - n 3
где во второй формуле 1 = 2 и 3 , в третьей формуле 3 с 1, а знак || || обозначает евклидово расстояние.
Первые две операции «слияния»/«разделения» обеспечивают обратимое слияние кластеров для фиксированного иерархического множества кластеров или сегментов, вычисляемой формы и размеров. Третья операция «коррекции» состоит в реклассификации пикселей из одного кластера в другой, что влечет модификацию иерархического множества кластеров пикселей изображения.
Три перечисленных операции порождают множество алгоритмов получения квазиоптимальных приближений изображения.
Критичной и определяющей по скорости обработки является первоначальная генерация приближений изображения, которая в модели выполняется в методах итеративного слияния кластеров пикселей или смежных сегментов изображения, выбираемых по критерию минимизации приращения суммарной квадратичной ошибки A E merge :
A E merge ( 1, 2 ) = min .
Логически самым простым методом, позволяющим при этом сразу получить выпуклую иерархическую последовательность приближений изображения, является метод Уорда [15], в котором анализируются всевозможные пары кластеров пикселей. Однако, расчеты методом Уорда занимают много времени, особенно, в случае изображений большого размера. Для снижения вычислительной сложности при минимизации A Emerge анализируют и объединяют друг с другом только смежные сегменты, как в модели Мамфорда-Шаха [6, 7], что приводит к нарушению выпуклой зависимости ошибки аппроксимации E от числа сегментов и снижает эф- фективность ее минимизации, особенно при малом числе сегментов. Для достижения компромисса методы обработки по Мамфорду-Шаху и по Уорду выполняются один за другим, что снижает детализацию изображения до ограниченного числа суперпикселей [9-12]. Для развития модели квазиоптимальных приближений без снижения общности рассуждений в настоящее время реализуется метод комбинированной сегмента-ции/кластеризации, в котором метод кластеризации Уорда применяется для «редакции» сегментации по Мамфорду-Шаху из условия сохранения выпуклости последовательности значений E .
Для минимизации суммарной квадратичной ошибки в рамках модели квазиоптимальных приближений разработаны методы улучшения кластеризации и сегментации изображения, которые разделяются на два типа — глобальные и локальные.
При глобальном улучшении сегментации суммарная квадратичная ошибка снижается за счет циклического разделения надвое сегмента 1 в одном месте изображения с одновременным слиянием пары смежных сегментов 2 , 3 в другом месте по критерию уменьшения суммарной квадратичной ошибки:
AEdvide (1)+ AEmerge (2,3)< 0, где предполагается, что все три сегмента различны.
Метод назван SI -методом (Segmentation Improvement method). Одна версия метода предусмотрена для улучшения отдельного приближения изображения [10-12], другая — для улучшения иерархической последовательности приближений в целом [9]. Основное преимущество SI -метода состоит в том, что он эффективно справляется с улучшением грубой сегментации.
При локальном улучшении сегментации сегменты поглощают части смежных. Критерием выполнения исключения пикселей сегмента 3 из состава пикселей сегмента 1 и включения их в состав сегмента 2 , смежного с сегментом 3 , служит условие отрицательного приращения суммарной квадратичной ошибки:
^ E correct < 0 .
По существу, метод локального улучшения сегментации является усиленной версией метода K -средних в современной интерпретации [16]. Однако он эффективен только при условии предварительного глобального улучшения качества [9-12].
4. Структура данных
В модели квазиоптимальных приближений изображения все вычисления проводятся в терминах деревьев Слейтора-Тарьяна, к которым в настоящее время добавляются адресные списки, заданные в виде циклов [9,12]. Вместе они образуют «динамическую» сеть, которая «набрасывается» на пиксели для ускорения вычислений и экономии памяти (рис. 2).
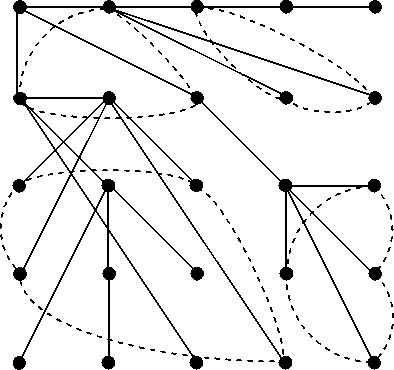
Рис. 2. Структура данных на основе динамических деревьев и циклов.
Циклы на рис. 2 обозначены пунктирными линиями.
На самом деле, машина работает не с пикселями, изображениями или объектами в матричном виде, а с массивами деревьев и массивами циклов, что достигается благодаря специально разработанному программно– алгоритмическому обеспечению вычислений в терминах деревьев Слей-тора-Тарьяна. Характерно, что в отличие от традиционной интерпретации, при интерпретации деревьев по Слейтору-Тарьяну бинарная иерархия множеств описывается не бинарным, а нерегулярным деревом с произвольной структурой, что позволяет использовать их в контексте рассматриваемых задач квазиоптимальной аппроксимации изображения.
Благодаря использованию динамических деревьев Слейтора-Тарьяна снимаются ограничения по памяти и обеспечивается ускорение вычислений не менее, чем в 100 раз. Эффект применения сети на основе динамических деревьев достигается за счет того, что:
- метаданные, которые задают иерархическое множество кластеров, размещаются на том же множестве координат, что и сами данные;
- реализуется обобщенный механизм обратимых вычислений, когда любую стадию вычислений можно не только восстановить, но и получить в модифицированном виде, что особенно полезно при минимизации суммарной квадратичной ошибки E .
5. Результаты эксперимента
Развитие сетевой технологии решения проблемы сегментации посредством квазиоптимальных приближений изображения расширяет классическую область применения теории графов. С практической точки зрения, динамические сети на основе деревьев Слейтора-Тарьяна интересны тем, что, со временем, могут составить альтернативу общеупотребительным нейронным сетям и оказаться полезными при изучении механизмов зрительного восприятия человека и других живых систем.
Рис. 3 на примере стандартного цветового изображения иллюстрирует преобразование любой иерархической последовательности приближений изображения в иерархическую последовательность квазиоптимальных приближений.

37,08620
40,95321
34,94496

30,49064
21,32865 18,08022
Рис. 3. Приближения изображения с 2, 3, 4 сегментами (вверху) и, соответственно, в 2, 3, 4 цветах (внизу).
Верхний ряд на рис.3 иллюстрирует иерархическую сегментацию в модели Мамфорда-Шаха, полученную итеративным слиянием смежных сегментов [6,7]. В нижнем ряду показана квазиоптимальная кластеризация пикселей изображения, индуцированная реструктуризацией множеств пикселей, которые составляют сегменты изображения, вычисленные по Мамфорду-Шаху. Под приближениями выписаны значения среднеквадратичного отклонения σ приближения от изображения.
Алгоритм состоит в том, что при слиянии сегментов, сопровождающемся убыванием приращения суммарной квадратичной ошибки, они сначала разделяются на части, которые затем соединяются в целое методом Уорда. В результате итеративного слияния/разделения возникающих кластеров формируется множество из 2 N - 1 кластеров пикселей, которые затем SI –методом [9] упаковываются в результирующую иерархическую последовательность из N приближений, описываемых выпуклой последовательностью значений ошибки аппроксимации E .
Графики на рис. 4 позволяют оценить эффект преобразования приближений из связных сегментов изображения по Мамфорду-Шаху (верхняя пунктирная кривая) в квазиоптимальные приближения обсуждаемым методом комбинированной сегментации/кластеризации (нижняя сплошная кривая).
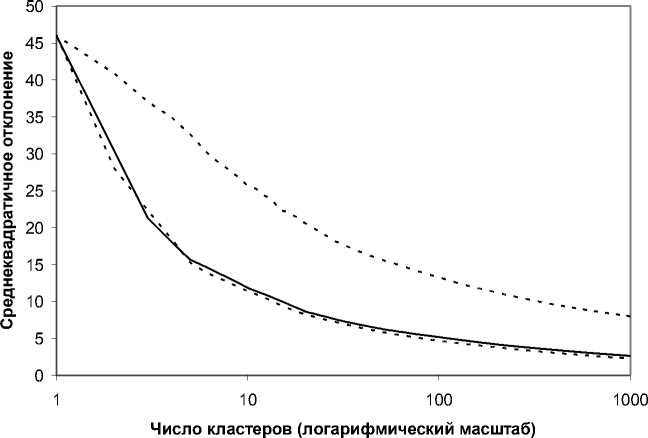
Рис. 4. Зависимость среднеквадратичного отклонения σ от числа кластеров g в диапазоне от 1 до 1000.
Нижняя пунктирная кривая описывает кластеризацию пикселей методом Уорда. Она переплетается со сплошной кривой, построенной для метода комбинированной сегментации/кластеризации. Однако если в предложенном методе сегментации/кластеризации метод Уорда применяется к тысячам кластеров пикселей, возникающих при разделении сегментов, то в оригинальном методе Уорда приходится анализировать сотни тысяч кластеров. Поэтому, наш метод существенно более перспективен для скоростной обработки.
В целом применение модели квазиоптимальных приближений для решения проблемы сегментации перспективно тем, что позволяет создавать алгоритмы для устойчивого автоматического выделения заранее не установленных объектов [11].
Заключение
В статье подытожены результаты исследований по проблеме автоматического выделения объектов на цифровом изображении. Проблема возникла одновременно с обработкой изображений и до сих пор с ней сталкивается практически каждый программист, занимающийся машинным зрением. Если раньше при унификации решений для выделения и распознавания объектов упор делался на создание программ, ориентированных на обучение специалистом-предметником, то сейчас наметилась тенденция разработки специального программного инструментария, рассчитанного на использование инженером-программистом. Роль последнего сводится к установлению соответствия между объектами, которые «видит» компьютер и объектами, которые видит человек. При этом решающее значение может иметь не применение сложившегося разнообразия подходов и решений, а проработанная единая модель низкоуровневого машинного зрения, которая совершенно необходима для исключения проб и ошибок, как при постановке, так и при решении задачи. По всей видимости, уже через несколько лет сегментация изображений станет предметом исследования немногочисленных команд профессионалов, а остальные специалисты будут пользоваться готовыми программными продуктами, подобно тому, как в настоящее время пользуются готовыми программами сжатия «без потерь».
За решением проблемы автоматического выделения объектов, вероятно, последует эффективное решение проблемы сжатия «с потерями» при условии минимизации потерь в модели квазиоптимальных приближений или другой эффективной модели.
Список литературы Основы модели квазиоптимальных приближений изображения
- Sleator D.D., Tarjan R.E. Self-Adjusting Binary Search Trees//Journal of the ACM. -1985. -Vol. 32.-№ 3. -P. 652-686.
- Харинов М.В. Разработка динамических структур данных системы автоматизированного распознавания изображений/руков. B.В. Александров/Автореф. Дис. канд. технич. наук. -СПб., 1993. -20 с.
- Nock R., Nielsen F. Statistical Region Merging//IEEE Trans. Pattern Anal. Mach. Intell. -Vol. 26(11). -2004. -P. 1452-1458.
- Харинов М.В. Запоминание и адаптивная обработка информации цифровых изображений/Под ред. Р.М. Юсупова. -СПб.: Изд-во C.Петерб. ун-та, 2006. -138 с.
- Харинов М.В. Обобщение трех подходов к оптимальной сегментации цифрового изображения//Труды СПИИРАН. -2013. -Вып. 2(25).-С. 294-316.
- Mumford D., Shah J. Boundary detection by minimizing functionals, I//Proceedings of IEEE Computer. Vision Pattern. Recognition Conference. -San Francisco, 1985. -P. 22-26.
- Bar L., Chan T.F., Chung G., Jung M., Vese L.A., Kiryati N., Sochen N. Mumford and Shah Model and Its Applications to Image Segmentation and Image Restoration//Handbook of Mathematical Methods in Imaging. -2015.-P. 1539-1597.
- Toffoli T. Reversible computing. -Springer Berlin Heidelberg. -1980. -P. 632-644.
- Kharinov M.V. Pixel Clustering for Color Image Segmentation//Programming and Computer Software.-2015. -Vol. 41.-№. 5. -P. 258-266.
- Kharinov M.V. Model of the quasi-optimal hierarchical segmentation of a color image//Journal of Optical Technology.-2015. -Vol. 82.-Issue 7.-P. 425-429.
- Харинов М.В., Ханыков И.Г. Комбинированный метод улучшения сегментации изображения//Вестник Бурятского государственного университета. -Вып.9. Математика и информатика.-2015. -С. 118-124.
- Харинов М.В., Ханыков И.Г. Оптимизация кусочно-постоянного приближения сегментированного изображения.//Труды СПИИРАН. -2015. -Вып. 3(40). -С. 183-202.
- Айвазян С.А., Бухштабер В.М., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Классификация и снижение размерности//М.: Финансы и статистика, 1989. -607 с.
- Redding N.J., Crisp D.J., Tang D.H., Newsam G.N. An efficient algorithm for Mumford-Shah segmentation and its application to SAR imagery//Proc. Conf. Digital Image Computing Techniques and Applications (DICTA’99). -1999. -P. 35-41.
- Ward J.H., Jr. Hierarchical grouping to optimize an objective function.//J. Am. Stat. Assoc. -1963. -Vol. 58.-Issue 301. -P. 236-244.
- Dvoenko S.D. Meanless k-means as k-meanless clustering with the bipartial approach//Pattern Recognition and Information Processing (PRIP’2014)/Proc. of the 12th Int. Conf.-Minsk, 2014. -P. 50-54.


