ОСНОВЫ ВЗАИМОДЕЙСТВИЯ ОДНОКОМПОНЕНТНОГО СФЕРИЧЕСКОГО ДАТЧИКА НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ, ИМЕЮЩЕГО РАЗОМКНУТУЮ СИСТЕМУ ЭЛЕКТРОДОВ, С ОДНОРОДНЫМ ПОЛЕМ

По результатам анализа технической литературы [1–4], установлено, что известные датчики напряженности электрического поля (ЭП), используемые для контроля и измерения напряженности низкочастотных ЭП высоковольтного оборудования, — это электроиндукционные датчики, основанные на электростатической индукции.

В основе таких датчиков лежат проводящие тела различных геометрических форм, простейшими из которых являются куб, цилиндр и сфера. Эти проводящие тела одновременно служат и датчиком, и чувствительным электродом, поскольку они своей поверхностью воспринимают электрический заряд, пропорциональный напряженности ЭП. Для снятия электрических зарядов с проводящих поверхностей тел датчиков используются дополнительные проводящие электроды, расположенные вблизи поверхности тел. Для того чтобы электроды были частью поверхности проводящих тел датчиков, их размещают на малом расстоянии от поверхности тел и используют измерительные цепи с входным импедансом, близким к нулю. Такие датчики называются датчиками с замкнутой системой электродов [5–8].

В данной работе будут рассматриваться теоретические основы построения датчиков с разомкнутой системой электродов, представляющих собой тонкие оболочки в форме полых сферических сегментов, и их взаимодействие с однородным ЭП.

ПОСТАНОВКА ЗАДАЧИ

Для создания теоретических основ построения датчиков напряженности ЭП со сферическими электродами разомкнутой системы необходимо решить ряд задач:

• 1)    проанализировать и обобщить известные методы расчетов взаимодействия двух проводящих сферических оболочек с однородным ЭП;

• 2)    установить аналитически или численными методами зависимость электрических зарядов, индуцированных на поверхности сферических оболочек, от их геометрических размеров;

• 3)    установить аналитически или численными методами зависимость разности потенциалов между сферическими оболочками от их геометрических размеров;

• 4)    установить аналитически или численными методами зависимость электрической емкости

между сферическими оболочками от их геометрических размеров;

• 5)    по полученным результатам предложить конструктивное решение однокомпонентного сферического датчика напряженности ЭП с разомкнутой системой электродов;

• 6)    провести анализ возможных выходных сигналов датчика и выбрать наиболее приемлемый для датчика с разомкнутой системой электродов;

• 7)    составить математическую модель и провести математическое моделирование, по результатам которого

  – получить эмпирические формулы, связывающие электрический заряд, напряжение холостого хода и емкость между электродами датчика с их угловыми размерами,

  – обосновать выбор оптимальных размеров электродов датчика.

ТЕОРИЯ

В основе теории сферического датчика напряженности ЭП с разомкнутой системой электродов лежат фундаментальные работы [9–12], а также статьи [13–15].

Система электродов датчика состоит из двух тонких проводящих сферических оболочек S ₁ и S ₂ в форме сферических сегментов, являющихся частью сферы радиуса R . Диэлектрические проницаемости сред вне и внутри сферических оболочек

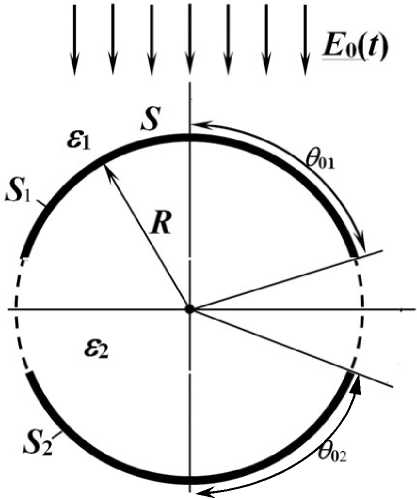
Рис. 1. Система сферических электродов для исследования в электрическом поле.

соответственно равны ε 1 и ε 2 . Далее сферические оболочки в форме сферических сегментов будем называть электродами или чувствительными электродами (ЧЭ). Сферические электроды расположены соосно на диаметрально противоположных сторонах условной сферы, и их размеры задаются угловыми размерами θ ₀₁ и θ ₀₂, отсчитываемыми от одной оси датчика (рис. 1).

При рассмотрении поведения такой системы проводящих ЧЭ в ЭП необходимо учесть следующие условия:

– первое условие исходит из того, что все точки поверхности проводящих электродов должны иметь равные потенциалы, отсюда следует

А ф =0; (1)

– второе условие задает потенциалы поверхностей электродов ф S1 = Фо1 и ф5 2 = Фо2; (2)

– третье условие утверждает, что при переходе границ диэлектрик–проводник и проводник– диэлектрик вектор электрического смещения не должен изменяться

D r i = _£ 1 E r i = 8 1 '^ф r = r = я ( S , ); (3) d r

Dr 2 = 8 2 Er 2 = 8 2 ^ r=R = ^( S2), (4) dr где Er1 и Er2 — нормальные составляющие вектора напряженности ЭП на поверхности ЧЭ S1 и S2; σ(S1) и σ(S2) — поверхностные плотности зарядов на электродах S1 и S2.

С учетом этого при помещении системы прово-дящихЧЭ в однородное ЭП на их поверхности индуцируются электрические заряды, определяемые выражением [9]

q = f я ( S )d S , (5)

S где σ(S) — поверхностная плотность заряда, определяемая для сферических оболочек из выражения [10]

28 ”<

^{я (} S 1 ) =    E l n +7 I AP ^{(cos 9} )’

R n=0 к

я ( S 2 ) = 8 E | n + 7 I B n P (cos ⁹ )

R n=0 к

Здесь

θ ₀₁

An = J fl (9)cos

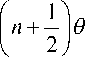
d θ

и

π

B _n = J f 2 ( 9 )sin

θ 02

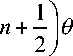
d θ

коэффициенты,

определяемые через функции f 1 ( θ ) и f 2 ( θ ); P _n (cos θ ) — полиномы Лежандра; n — порядковый номер полиномов Лежандра, принимающий значения от 0 до да ; d S = R ² sin - d в — элемент поверхности ЧЭ.

После подстановки (6) в (5) и преобразований получим выражения для зарядов на первом и втором электроде [8]:

θ ₀₁

q— = 4ns о R f ( - )cos - d в ,        (7)

πθ q 2(в0) = 4nsR\ f2.(0 )sin d в,          (8)

где f 1 ( θ ) и f 2 ( θ ) — функции, пропорциональные плотности поверхностного заряда на ЧЭ в форме сферических сегментов [10], получаемые из решения системы парных интегральных уравнений:

где ϕ 01 и ϕ 02 — потенциалы проводящих ЧЭ S 1 и S ₂; ε * = ε ₂ / ε ₁ — отношение диэлектрических проницаемостей сред вне и внутри ЧЭ датчика.

Электрические заряды, определяемые выражениями (7) и (8), пропорциональны диэлектрической проницаемости ε 1 среды, окружающей ЧЭ, площади поверхности ЧЭ и напряженности ЭП E ₀ [16–18]

q ( t ) = ks 1 SE ₀( t ). (10)

Разность потенциалов ϕ 01 и ϕ 02 проводящих ЧЭ определит напряжение холостого хода

U xx⁽ t ) = % 01⁽ t ) — % 02⁽ t ),                 ⁽¹¹⁾

которое также будет пропорционально напряженности ЭП E 0 ( t )

U xx ( t ) = C = kCS E o ( t ),               (1 ² )

ff—+

+<

^- %

2 + s*

π

1 + 2 s *

3 cos θ ,

d t > =

где C — электрическая емкость, образованная ЧЭ 1 и 2.

Электрическая емкость может быть определена из выражения [12]

θ 01

f1

_C = 4_mR ¹ - ²J ^{f ( - )s} in^d ^- ,

f _;( - o ) +

+<

π

% 2

2 + s *

1 + 2 s *

3 sin₂ θ ₀,

d t > =

где функция f ( θ ) определяется решением системы интегральных уравнений (9) [19].

В соответствии со сформированными теоретическими основами применительно к датчику напряженности ЭП, построена его эквивалентная электрическая схема замещения (рис. 2).

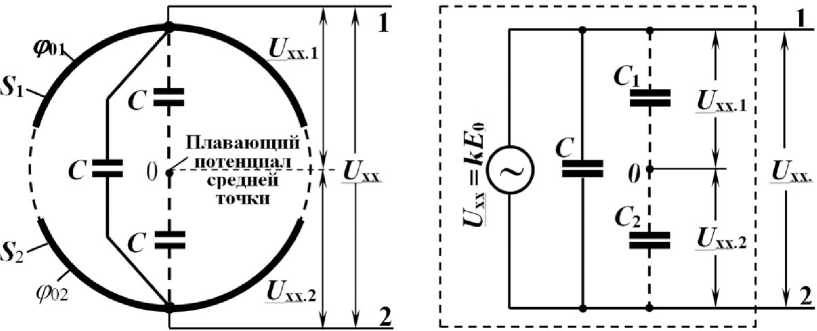
Рис. 2. Схемы замещения датчика.

а — конструктивная, б — эквивалентная электрическая схемы

На рис. 2 C = С д — виртуальная электрическая емкость, образованная ЧЭ S 1 и S 2 и определяемая из выражения (13); C ₁ = C ₂ = 2 С — виртуальные электрические емкости между соответствующими ЧЭ датчика и его плавающей средней точкой. Электрические емкости C , C 1 и C 2 связаны соотношением C = ( С 1 C 2 )/( С 1 + C 2 ) .

Выражения (5)–(13) будут положены в основу математической модели однокомпонентного сферического датчика напряженности ЭП с разомкнутой системой ЧЭ.

СФЕРИЧЕСКИЙ ДАТЧИК С РАЗОМКНУТОЙ СИСТЕМОЙ ЧУВСТВИТЕЛЬНЫХ ЭЛЕКТРОДОВ

В работе сферический датчик с разомкнутой системой ЧЭ будет рассматриваться на примере однокомпонентного датчика. Датчики такого типа рассмотрены в работах [1–4] без теоретического обоснования. Одно из возможных конструктивных решений построения такого датчика схематично показано на рис. 3.

Датчик состоит из двух одинаковых зеркально отображенных проводящих ЧЭ 1 и 2, представляющих собой сферические оболочки, выполненные в форме сферических сегментов радиуса R с угловым размером θ 0 . ЧЭ датчика изготавливаются из проводящих материалов с высокой электрической проводимостью. Их располагают соосно на одной координатной оси на поверхности диэлектрического основания 3, имеющего форму сферы, радиуса r , меньшего R на величину δ , соответствующую толщине стенки диэлектрического основания датчика. ЧЭ могут быть наклеены или

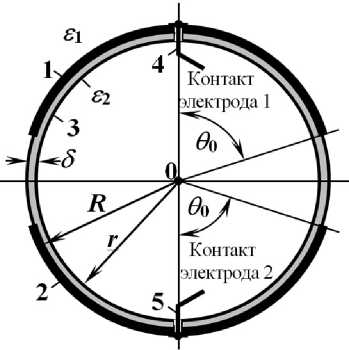
Рис. 3. Однокомпонентный сферический датчик с открытой системой чувствительных электродов.

нанесены методом напыления на диэлектрическое основание. Толщина стенки диэлектрического основания выполняется согласно условию δ ≪ R . Для диэлектрической проницаемости диэлектрика основания датчика должно выполняться условие £ 2 >  £ 1 , где £ 1 — диэлектрическая проницаемость среды, в которой будет использоваться датчик. От ЧЭ 1 и 2 вдоль координатной оси выведены контакты 4 и 5 для подключения датчика к измерительной цепи.

ИЗМЕРИТЕЛЬНАЯ ЦЕПЬ ДАТЧИКА С РАЗОМКНУТОЙ СИСТЕМОЙ

ЧУВСТВИТЕЛЬНЫХ ЭЛЕКТРОДОВ

Для датчика с разомкнутой системой ЧЭ можно рассматривать два возможных вида выходных электрических сигналов.

– Электрический заряд, индуцированный ЭП на каждом ЧЭ датчика. Его, согласно выражению (10), для каждого электрода можно записать, как qi(t) = k£i Si Eo(t), q2(t) = k£ S2 Eo(t),

где k — коэффициент пропорциональности, зависящий от формы и размеров ЧЭ, он определяется вы-3θ ражением k = ^tgy (его вывод ниже); £1 — диэлектрическая проницаемость среды; S1 и S2 — площади поверхности ЧЭ датчика (в рассматриваемом случае для сферических сегментов Si = S2 = S = 4nR2 sin2 (0o/2)); E0( t) — напряженность ЭП при отсутствии в поле ЧЭ.

– Разность потенциалов ( ϕ ₁ – ϕ ₂) между ЧЭ 1 и 2

датчика равна напряжению холостого хода, и, согласно выражению (12), его можно записать

U _x( t ) = q ( t ) = k^S E ( t ), xx                          0

дд

где С д = С — емкость датчика, определяющаяся системой ЧЭ 1 и 2 (см. рис. 2).

В зависимости от вида выходных сигналов будут различаться и входные измерительные цепи датчика. Так, например, для снятия электрического заряда с поверхности ЧЭ необходимо проинтегрировать ток короткого замыкания q (t) = J i K3( t )d t,(16)

где ток короткого замыкания определяется выражением i“(t)=dqT) = teis dET) •(17)

dtd

Из выражения (17) следует, что ток i кз ( t ) пропорционален не напряженности ЭП E 0 ( t ), а скорости его изменения d E 0 ( t ) / d t . Если учесть, что напряженность ЭП изменяется по синусоидальному закону, то скорость ее изменения будет изменяться по закону косинуса, поэтому ток короткого замыкания также может быть информативным сигналом датчика.

Отличия снятия тока короткого замыкания iкз (t) от снятия напряжения холостого хода Uxx (t) заключаются в обеспечении необходимого входного импеданса измерительной цепи. Так, при снятии с ЧЭ датчика тока короткого замыкания iкз (t) требуется измерительная цепь, имеющая входной импеданс, в идеале, равный нулю. А для снятия с датчика напряжения холостого хода Uxx (t) требуются входная измерительная цепь с высоким входным импедансом, в идеале, равным да. Высокий входной импеданс не будет нагружать датчик и обеспечит снятие с него напряжения, равного напряжению Uxx(t). Анализ выявленных выходных сигналов датчика с разомкнутой системой ЧЭ показывает неприемлемость использования в качестве выходного сигнала датчика токового сигнала в виде тока короткого замыкания iкз(t). Это связано с тем, что низкий входной импеданс измерительной цепи закоротит разнесенные в пространстве ЧЭ, находящиеся под разными потенциалами. Поэтому такое использование измерительной цепи приведет к искажению ЭП. В связи с этим единственным выходным сигналом датчика с разомкнутой системой ЧЭ остается напряжение холостого хода Uxx (t). Однако и его использование не лишено недостатков, одним из которых, как следует из выражения (15), является зависимость Uxx (t) от емкости Cд. В связи с открытостью системы электродов на Cд будут оказывать влияние множество внешних факторов. С учетом сказанного можно прийти к выводу о необходимости калибровки каждого датчика.

Одна из возможных измерительных цепей для снятия напряжения U xx ( t ) в упрощенном виде представлена на рис. 4.

В основе входной измерительной цепи лежит дифференциальный усилитель с общим проводом, не связанным с плавающим потенциалом средней точки датчика. Дифференциальные входы измерительной цепи выполнены с высоким входным импедансом порядка 100 кОм. На выходе измерительной цепи вырабатывается напряжение U вых. ( t ), пропорциональное U xx ( t ), а следовательно, напряженности ЭП E ₀( t ). Измеряя напряжение на выходе измерительной цепи, например, цифровым вольтметром, можно определить напряженность исходного поля.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И ЕГО РЕЗУЛЬТАТЫ

Полученные теоретические положения, описанные в краткой теории, легли в основу составления математической модели датчика, состоящего из двух независимых сферических оболочек в форме сферических сегментов. В основу математической модели положены выражения (7)–(17) и сделанные нормировки:

– для электрического заряда q ' =

^q πε ₁ R ² E ₀ ^;

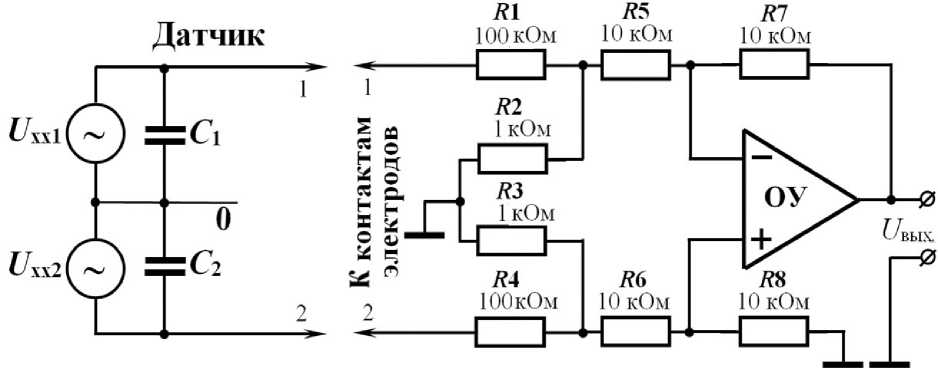
Рис. 4. Входная измерительная цепь датчика.

– для напряжений холостого хода

U ′ = ^Uxx , U ′ = U ′ = ^Uxx ; xx            , xx 1        xx 2

E ₀ R              2 E ₀ R

– для электрической емкости

с

C ′ = ^C .                  (20)

πε ₁ R

Математическая модель позволяет решить систему интегральных уравнений (9) путем преобразования их к системе алгебраических уравнений и по результатам ее решения найти электрические заряды (7), (8), индуцированные на поверхности электродов, напряжение холостого хода (11) и емкость электродов (13). Математическая модель составлялась с учетом того, что датчик находится в однородном ЭП.

Математическая модель позволила объединить:

– параметры взаимодействия датчика с ЭП, к которым отнесены электрические заряды q ( t ), напряжение U xx ( t ) и емкости C , C 1 и C 2 ;

– конструктивные параметры датчика, к которым отнесены радиус R ЧЭ и их угловые размеры θ 0 ;

– параметры среды, окружающей ЧЭ датчика, к которым отнесены диэлектрические проницаемости ε 1 и ε 2 с внешней и внутренней стороны сферических сегментов.

В результате математического моделирования получены численные значения основных электрических параметров датчика с разомкнутой системой ЧЭ, представленные в таблице. Полученные данные расчетов положены в основу построения графиков зависимостей q ′ ( θ 0 ), С ′ ( θ 0 ) и U ′ хх ( θ 0 ) и их дальнейшего анализа.

Анализируя представленные в табл. численные значения, можно установить, что график, построенный по нормированным значениям электрического заряда q′(θ0) хорошо согласуется с полученным опытным путем эмпирическим выражением q′(θ0) =3sinθ0 . (21)

Тогда с учетом нормировки (19) электрический заряд, индуцированный на электродах датчика можно описать эмпирическим выражением

q ( θ ₀) = q ′ ⋅ πε ₁ R ² E ₀ = 3 πε ₁ R ² sin θ ₀ E ₀. (22)

Согласно выражению (15), заряд пропорционален поверхностной площади электродов S, диэлектрической проницаемости среды ε1 и напряженности ЭП E0. С учетом этого можно записать kε1S E0 = 3πε1R2sinθ0 E0.

Табл. Расчетные значения конструктивных и электрических параметров датчика

θ 0	q′ 1 = –q′ 2	C 1′ = C 2′	C ′	U ′ xx	U ′ xx1 = U ′ xx2
5	± 0.28662	0.28832	0.14416	1.98821	0.99411
10	± 0.54739	0.55524	0.27762	1.97172	0.98586
15	± 0.74787	0.77008	0.38504	1.94232	0.97116
30	± 1.43297	1.56491	0.78242	1.82384	0.91192
45	± 2.05212	2.55672	1.27836	1.60528	0.80264
60	± 2.58226	3.87282	1.93641	1.33189	0.66594
70	± 2.87327	5.40428	2.70214	1.06333	0.53167
75	± 2.89727	6.42484	3.21242	1.00523	0.50262
80	± 2.99765	7.17316	3.58658	0.83579	0.41789
85	± 2.99862	9.21148	4.60574	0.65106	0.32553
90	± 3.00277	12.46322	6.23161	0.48186	0.24093

Тогда, учитывая площадь электрода θ

S = 4nR^sin2y, определим коэффициент пропорциональности, как k = 2ctg ^               (23)

Ранее выражение для этого коэффициента не было известно.

Анализ графика U'_xx(0₀), построенного по численным значениям таблицы, показывает его хорошую согласованность с эмпирическим выражением, состоящим из двух слагаемых

U Х О = ( 3cos ( o + 1 ) /2.         (24)

С учетом нормировки (19) можно записать

U Ш = 2 ( 3cos ^ 0 + 1 ) RE о .     (25)

Можно предположить, что первое слагаемое определяет потенциал электрода датчика в ЭП, а второе — потенциал точки пространства, совпадающей с вершиной электрода в отсутствии поля относительно центра датчика.

Зная выражения для заряда q ' (^) и U_xx(0₀), несложно установить эмпирическую зависимость емкости C '( 0 _о) электродов датчика в форме сферических сегментов от их углового размера θ ₀:

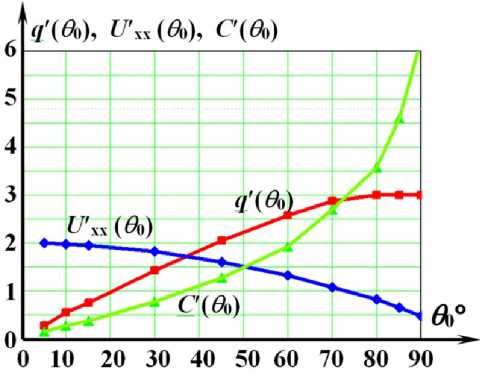
Рис. 5. Графики зависимостей заряда q '( ( )), емкости С '( 0 0 ) и напряжения холостого хода U _хх ( 0 >) от углового размера θ 0 электродов датчика, построенные по эмпирическим выражениям (21), (24), (26), и расчетные табличные точки.

C Ж) = Y⁶^ .         (26)

3cos 0 ₀ + 1

С учетом (20) и (24) емкость C определится, как sin

C0 o ) = 6п£ 1 R  ---0  .         (27)

• 3 cos ( ₀ + 1

График изменения емкости C'((О) от углового размера электродов датчика, построенный по точкам таблицы, хорошо согласуется с выражением (26). Для сравнения построены графики q '( ( ,), С '( ( ₀) и U _хх( ( ₀) по полученным эмпирическим выражениям (21), (24) и (26) и на них проставлены табличные расчетные точки (рис. 5).

Из графиков рис. 5 можно предположить, что оптимальные угловые размеры чувствительных электродов датчика должны лежать в диапазоне 30 °< 0₀ <  60 ° . Это объясняется тем, что с ростом углового размера θ ₀ чувствительных элементов напряжение холостого хода, являющееся выходным сигналом датчика, уменьшается.

Таким образом, математическое моделирование датчика напряженности ЭП с разомкнутой системой ЧЭ в однородном поле позволило установить характер изменения основных электрических параметров датчика q ( θ 0 ), С ( θ 0 ) и U хх ( θ 0 ) в зависимости от углового размера θ ₀ его ЧЭ и получить эмпирические выражения этих зависимостей.

ВЫВОДЫ И ЗАКЛЮЧЕНИЕ

Результаты исследования позволяют сделать следующие выводы.

• 1.    Разработаны теоретические положения взаимодействия двух незамкнутых диаметрально противоположных сферических оболочек в форме сферических сегментов с однородным ЭП.

• 2.    Теоретические положения позволили предложить одну из возможных конструкций однокомпонентного сферического датчика напряженности ЭП с разомкнутой системой электродов и установить взаимосвязь его электрических и конструктивных параметров.

• 3.    Установлены возможные виды выходных сигналов датчика, к которым отнесены электрический заряд q ( t ), напряжение холостого хода U xx ( t ) и ток короткого замыкания i _кз.

• 3.    Проведен анализ возможных видов выходных сигналов датчика. Анализ показал непригодность использования электрического заряда и тока короткого замыкания в качестве выходных сигналов датчика. Это требует для их снятия применение измерительной цепи с близким к нулю входным импедансом, приводящим к замыканию электродов между собой и, как следствие, к искажению поля.

• 4.    Единственно возможным выходным сигналом датчика с разомкнутой системой электродов является напряжение холостого хода U xx ( t ). Использование в качестве выходного сигнала напряжения холостого хода требует применения измерительной цепи с высоким входным импедансом.

• 5.    Предложен один из возможных вариантов построения измерительной цепи на основе операционного усилителя с высоким входным импедансом.

• 6.    Проведено математическое моделирование однокомпонентного сферического датчика напряженности с разомкнутой системой электродов в однородном ЭП. Результатом моделирования являются графики зависимости электрических параметров датчика q ( θ 0 ), С ( θ 0 ) и U хх ( θ 0 ) от углового размера θ 0 его электродов.

• 7.    Впервые получены эмпирические выражения для электрических параметров датчика с разомкнутой системой электродов:

  – для электрического заряда (см. выражение (22));

  – для напряжения холостого хода (см. выражение (25));

  – для электрической емкости между электродами (см. выражение (27)).

• 8.    Полученные эмпирические выражения могут быть положены в основу оценочного расчета датчиков с разомкнутой системой электродов.

В заключение следует сказать, что получены новые знания по разработке датчиков напряженности ЭП с разомкнутой системой электродов в форме сферических сегментов.