Особенности динамики замкнутых электромехатронных преобразователей с шаговыми электродвигателями

Анализ устойчивости

Общим для работы замкнутого и разомкнутого ЭМТП с ШЭД является то, что независимо от амплитуды входного импульса ШЭД отрабатывает единичное шаговое перемещение, что эквивалентно наличию в структурной схеме порогового элемента, обладающего релейной характеристикой. Логическая часть электронного коммутатора (ЭК) осуществляет импульсную фазовую модуляцию, преобразуя одноканальную последовательность импульсов малой мощности в многофазную систему напряжений, прикладываемых к обмоткам управления ШЭД.1 Ступенчатому характеру напряжений на обмотках ШЭД соответствует дискретное вращение электромагнитного поля, вследствие чего движение ротора состоит из элементарных угловых перемещений, совершаемых по неко- торому закону. Электромехатронный преобразователь с ШЭД является системой с т+1 степенями свободы: т – электрические и одна механическая.

Эквивалентная структурная схема замкнутого ЭМТП с ШЭД представлена на рис. 1.2

Передаточная функция W л ( p ) в ЭМТП включает в себя передаточные функции интеллектуального силового модуля (ИСМ) и цифрового преобразователя перемещений (ЦПП), которые в первом приближении можно считать безинерционными и характеризовать коэффициентом передачи. В большинстве случаев влияние динамики циклического ЦПП можно учесть звеном чистого запаздывания. Динамические свойства ЦПП следящего типа рассмотрены в [1]. В зависимости от соотношения динамических показателей ШЭД и остальных звеньев ЭМТП, которые определяются построением

Смирнов Юрий Сергеевич – д-р техн. наук, профессор кафедры «Приборостроение», Южно-Уральский государственный университет; Тел: (351)2679012.

Рис. 1

ЭК и ЦПП, возможны два варианта определения условий устойчивости и возникновения периодических режимов в ЭМТП.

Первый вариант связан с применением в ЭМТП устройств, имеющих постоянные времени, значительно превышающие период управляющих импульсов ШЭД. Поэтому исследование устойчивости и условий возникновения периодических режимов может производиться путем перехода к эквивалентной релейной САУ без временного квантования. Это позволяет для анализа такой САУ воспользоваться известным методом гармонического баланса в его обычной форме.

В быстродействующих ЭМТП основным динамическим звеном является ШЭД. Анализ динамики такой САУ можно произвести на основе обобщенного метода гармонического баланса применительно к нелинейным импульсным системам.

Эквивалентная структурная схема ЭМТП для такого сочетания параметров представлена на рис. 2.

Импульсная переходная функция ЭМТП в данном случае будет переходной характеристикой ШЭД, которому соответствует переходная функция колебательного звена с запаздыванием, равным t _зап, поскольку входные импульсы ЭК можно считать дельта-импульсами. Для получения D-преобразования решетчатой функции с запаздыванием воспользуемся теоремой сдвига [2].

Переходная функция колебательного звена h (t) = 1 - e"! t/T х

х

cos

.

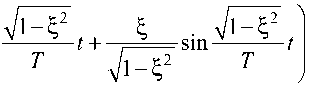
Без учета запаздывания это и есть импульсная переходная функция приведенной непрерывной части ЭМТП:

to ( t ) = 1 - e ^{! tT}

cos to t +

!

sin to t

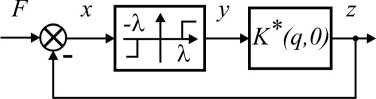
Рис. 2

где to =

71 -^!

T

Введем новую независимую переменную -безразмерное время t = t/T _y , тогда

Для анализа устойчивости определяем импульсную передаточную функцию разомкнутого ЭМТП, которая, как известно [2], представляет собой дискретное преобразование Лапласа импульсной переходной функции приведенной непрерывной части импульсной системы:

-! TJT to( t) = 1 - e    y/

! cos to t +—^

sin to t , (6)

^

K * ( q , е ) = D { to ( n , е ) } = Z e" qn to ( n , e ) .     (1)

n = 0

где to = to T_y.

Обозначим !Ty IT = n, тогда смещенная решетчатая функция to[n, е] = 1[n, е]-

Импульсную переходную функцию системы можно определить по известной передаточной функции, пользуясь теоремой разложения [2]:

- e "^{n n}

! cos ton + —f=

sin ton .

5 Г ” - 1

»(t )=zz v=0ц=0

( r v -И- 1 ) !

d r ^{-И- 1}

dp^r ” -ц- 1

Воспользуемся теоремами смещения и линейности и определим импульсную передаточную функцию комплекса без учета запаздывания:

t ^ц

^W ( P )( P ^- P v ) ” 1 e p = pv Ц !

. Pvt

/

K * ( q , e ) =

e q     e ^{2 q} cos toe- e q e ⁿ cos to ( 1 -e )

^^^^^^^—^^^^^^^— ^^^— eq - 1

e ^{2 q} - 2 e^qe ⁿ cos to+ e ^{2 n}

e "^ne -

где W ( p ) = P ( p )/ [ p^Q ( p ) ] .

Для случая, когда имеется один нулевой корень, С 0о = P (0)/ Q (0); C ” o = P ( p v )/ [ Q '( p v ) p v ] . (3) Вычисление коэффициентов С ” _ц довольно трудоемко. Импульсная переходная функция ю( t ) и переходная функция звена h ( t ) связаны между собой соотношением ю( t ) = dh / dt .

e2q sin toe + eqe n sin to(1 -e)E „„

___________________________i_____L !    e "ne.(8)

e2q - 2eq e"n cos to+e-2n

Чтобы получить импульсную передаточную функцию с учетом запаздывания, воспользуемся теоремой сдвига [2]. Если £ < 0, то введем в рассмотрение решетчатую функцию вида to(n-1, 1+s), тогда согласно теореме

D { to [ n- 1,1 + е ] } = e"^qF * ( q ,1 + е ) .

Особенности динамики замкнутых электромехатронных преобразователей с шаговыми электродвигателями

Выразим запаздывание через безразмерное время σ = tзап / Tу и воспользуемся теоремой запаздывания [2]. Импульсная передаточная функция ЭМТП (см. рис. 2) с учетом запаздывания будет иметь вид к * (q, e) =

e q     e ^{2 q} cos we - e q e ⁿ cos w ( 1 - e )

___________L e 'iE eq -1    e2q - 2eqe”n cos W+ e”2n

^^^^^M

^     e q sin w ( 1 -o ) + e ⁿ sin wo -n ( 1 -a )

1 - -^ 2 e ^{2 q} - 2 e^qe "ⁿ cos W+ e ²ⁿ

Учет влияния запаздывания важен при анализе устойчивости ЭМТП, она снижается с ростом запаздывания. Для анализа влияния запаздывания на устойчивость определяется импульсная передаточная функция замкнутого ЭМТП и по характе- ристическому полиному, с учетом критерия устойчивости Гурвица применительно к импульсным системам, определяется зависимость граничного коэффициента усиления системы как функция относительного запаздывания. По характеру эта зависимость является падающей, что указывает на ухудшение устойчивости системы с увеличением запаздывания [3].

Поскольку система является нелинейной, то необходимо определить условия отсутствия периодических режимов. Для этой цели используется метод Л.С. Гольдфарба, развитый в работах Я.З. Цыпкина и Ю.М. Коршунова применительно к нелинейным импульсным системам. Для получения условий отсутствия периодических режимов строятся их возможные границы. Упрощение анализа достигается использованием известного критерия абсолютной устойчивости САУ.

Построение переходного процесса

Для построения переходного процесса в системе удобно воспользоваться численным методом. В нелинейных непрерывных системах он обычно обеспечивает лишь приближенные решения, а для импульсных нелинейных систем во многих случаях дает точные решения. Для этого выводят рекуррентную формулу [3].

Преобразуем структуру ЭМТП к виду, показанному на рис. 3.

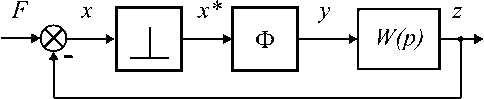
Рис. 3

Пользуясь обозначениями координат на нем, можно записать следующее уравнение:

^

F ( q ) - X ( q ) = K ‘( q ) £ Ф [ x ( n ) ] e " ^qn . (10) n = 0

Так как информация в D-преобразовании функции времени при ε = 0 содержится только в моменты времени t = nTy. то, следовательно, дан- ное уравнение содержит неизвестную величину ошибки при t = nTy, где Ту - период выборки информации, а n – номер управляющего импульса. Поскольку импульсная передаточная функция представляет собой D-преобразование импульсной переходной функции приведенной непрерывной части, ее можно разложить в ряд по степеням:

к * (q) = D {w[ n .0]} = g 0 + gie- q +

+ g 2 e " ² q + ... ,                                 (11)

где g k – ординаты импульсной переходной функции при t = K .

Аналогично входную функцию, равную нулю при отрицательных значениях времени, также можно разложить в степенной ряд:

F ( q ) = F 0 + F 1 e - ^q + F 2 e “^{2 q} + F₃ e "3 ^q +       (12)

Неизвестную функцию ошибки также представим степенным рядом:

X ( q ) = X ₀ + X 1 e - ^q + X ₂ e - 2 ^q + X ₃ e"^3q +. . . (13) где X k - величина ошибки при t = K .

При подстановке степенных рядов в исходное уравнение получим

[(F0 -X0) + (F -X1)e"q +(F2 -X2)-2q + .] =

= ( g 0 + g 1 e" q + g 2 e "2 q + . ) ( Ф [ X 0 ] +

+ Ф [ X 1 ] e" ^q + Ф [ X ₂ ] e "^{2 q} + . ) .           (14)

Чтобы удовлетворялось это уравнение, коэффициенты при соответствующих степенях е^q должны быть равны:

F 0 - x 0 = g 0 ф [ x 0 ] ;

F 1 - x 1 = g 0 ф [ x 1 ] + g 1 Ф [ x 0 ] ;

F 2 - x 2 = g 0 ф [ x 2 ] + g 1 Ф [ x 1 ] + g 2 ф [ x 0 ] ; (15)

F k - X k = ]£ g n Ф [ X k - n ] .

n = 0

Поскольку g 0 = 0, то, очевидно:

X 0 = F 0 ;

X 1 = F 1 - g 1 Ф [ X 0 ] ;

X 2 = F 2 - g 1 Ф [ X 1 ] - g 2 Ф [ X 0 ] ;

k

X k = F k - £ g n Ф [ X k _ „ ] , g 0 = 0.

n = 0

Поскольку коэффициенты g_k сходятся к постоянному значению, придется брать большое число слагаемых для получения достаточно точного результата. Чтобы избежать этого, произведем вычитание двух последовательных ошибок. В этом случае получим следующий вид выражений, определяющих ошибки:

X 1 = X 0 - &ф[ X 0 ] + F - F 0 ;

X 2 ^_ X i + F - F 1 - g 1^ф [ X i ] ^-( g ₂ - g i ) Ф [ X 0 ] ^;

X k + 1 ^_ X k ⁺ F k + 1 ^- F k ^{- g} 1 Ф ^[ X k ] ^-( g 2 ^- g i ) Ф X k - 1 .

Таким образом, переходный процесс в замкнутом ЭМТП при детерминированных входных воздействиях можно рассчитать по рекуррентной формуле [3]:

k

X k + 1 _ X k + F k + 1 - F k - E a n Ф [ X k - n ] . (18) n = 0

При ее выводе полагалось, что импульсная переходная функция в момент времени t = 0 имеет нулевое значение, а коэффициенты – a 0 = g 1 ; a 1 = g 2 – g 1 ; a k = g k +1 – g k . В этом случае коэффициенты а k при увеличении k будут стремиться к нулю. Коэффициенты g k можно либо вычислить путем деления числителя импульсной передаточной функции на ее знаменатель, либо взять ординаты импульсной переходной функции приведенной непрерывной части САУ в моменты времени t = kT у прихода управляющих импульсов на вход ЭМТП с ШЭД.

Построение переходного процесса в ЭМТП с ШЭД позволяет наглядно продемонстрировать основной недостаток пошагового управления, заключающийся в колебательном характере движения ротора и, соответственно, ИСМ. Находящиеся близко расчетные и экспериментальные значения параметров движения позволяют произвести оценку динамических показателей и ресурса ЭМТП с учетом оптимизации передаточного отношения ИСМ. Наименьшим ресурсом обладает ИСМ, имеющий износ поверхностей зацепления, т. е. редуктор.

Расчеты и экспериментальные исследования показали, что ЭМТП с ШЭД имеет области частот управления, при которых нагрузки на элементы ИСМ возрастают, что приводит к повышенному износу элементов редуктора. Кардинальным сред- ством устранения этого фактора является переход к минишаговому управлению. Наибольший эффект достигается при использовании минишагово-го управления в сочетании с самокоммутацией, что делает реальным создание безредукторного ЭМТП [4].

Это следует учитывать при проектировании ЭМТП с продолжительным сроком службы и переходить к безредукторным ЭМТП, которые за рубежом именуются Direct Drive (DD) [5], или Super Drive (SD).

При замыкании контура местной обратной связи (МОС) динамические свойства ЭМТП изменяются по сравнению с его динамическими свойствами при пошаговом управлении. Исполнительный электродвигатель при этом приобретает свойства вентильного электродвигателя (ВЭД), динамика которого требует отдельного рассмотрения.