Особенности фазовых траекторий в полной модели космологической эволюции на основе классического скалярного поля с хиггсовым потенциалом

В [1] были сформулированы основные математические соотношения космологической модели, основанной на. классическом скалярном Хиггсовом поле. Это, во-первых, нормальная автономная система, дифференциальных уравнений

Ф‘ = Z,(1)

Z‘ = -3hZ - еФ + атФ3,(2)

Ы = -ЗЫ - еф2 - 'Д + Am,(3)

где производные берутся по времени т = mt в комптоновских единицах, A_m = Ao - m⁴/4a_m, остальные обозначения см. в [2].

“The work is carried out in accordance with the Strategic Academic Leadership Program "Priority 2030"of the Kazan Federal University of the Government of the Russian Federation.

• ¹    E-mail: alsu sam@mail.ru

Во-вторых, это - уравнение гиперповерхности Эйнштейна. - Хиггса, являющееся, по сути, урав нением Эйнштейна 4 , с другой стороны - первым интегралом динамической системы (1) - (3):

Z ²   еФ² а_тФ4

"2     2” +  4

^{— Х}т = 0.

В третьих, это - соотношения для физических характеристик космологической модели: инвариантного космологического ускорения о 5 55 = 1 + Н ,(5)

а2Н инвариантной кривизны пространства Фридмана а =  Нгзк1 R^kl = Н2 V6(1 + fi2) 5 V6УН4 + (Н2 + Н)2 > 0,(6)

эффективной энергии динамической системы

£т(Ф,г) = ^ + е|2 - ^ + Хт > 0.(7)

Наконец, в-четвертых, это некоторые дифференциальные соотношения между динамическими переменными, являющиеся следствием полной системы уравнений Эйнштейна, и скалярного поля

Хиггса, в частности, эквивалентная форма, уравнения (5)

^‘ = —« 0),

согласно которому в космологической модели с классическим скалярным полем Хиггса, постоянная Хаббла, не может возрастать со временем.

Переходя к численному моделированию исследуемой динамической системы, заметим, во-первых, что некоторые существенные особенности поведения этой системы уже были выявлены на. основе численного моделирования в работе [3]. Следуя этой работе, динамическую систему (1) - (3) будем определять упорядоченным списком трех безразмерных параметров Р = [е, а_т,А_т] и упорядоченным списком начальных условий I = [I o ,Z o ,e], г де е = ±1, причем значению е = +1 соответствует фаза. расширения в начальный момент времени to. значенито е = —1 - фаза сжатия в этот момент времени. Согласно сказанному выше, начальное значение постоянной Хаббла, определяется уравнением Эйнштейна. (4), из которого имеем:

• ¹    . /^Г^¹  “т^ф4  , _ ^е Г^ о

^h0 = ± 2VT ⁺ ^      I ^{+ Хт} = 3 ^V£т•                    (⁹)

Во-вторых, заметим [3], что динамическая система. (1) - (3) является автономной системой обыкновенных дифференциальных уравнений, явно не зависящих от временной переменной, вследствие чего инвариантна по отношению к трансляции t ^ to + t . Поэтому в качестве начального момента времени при формировании начальных условий может быть выбрано любое значение to. Мы положим это значение, равным пулю. При этом мы вправе рассматривать и состояния динамической системы при отрицательных временах to < 0 .

В заключение перечислим основные результаты статьи.

• е    Космологические модели с классическим Хиггсовым полем в широком диапазоне фундаментальных параметров и начальных условий обнаруживают тенденцию переходить из режима, расширения (Н >  0) в режим сжатия (Н <  0);

• •    При этом имеются два режима скатывания Н+ ^ Н- в зависимости от геометрии гиперповерхности Эйнштейна, точнее говоря, от направления ее главной оси;

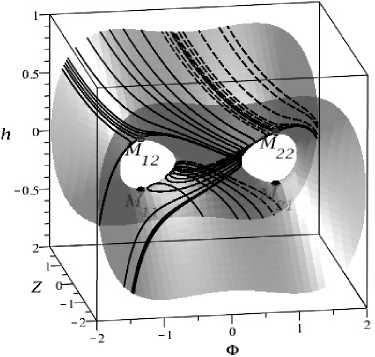
Рис. 1. Фазовые траектории динамической системы (1)-(3) для параметров Р = [1,1, -0.1] на. гиперповерхности Эйнштейна-Хиггса. начальные условия: Ф(0) = [-1.5, -1.47,-1.45,-1.425,-1.4,-1.25,-1, -0.7, -0.5, -0.25, -0.0001] - сплошные линии. Ф(0) = [0.0001,0.25,0.3,0.35,0.36,0.38,0.4,0.45,0.5,0.7,1,1.5] - пунктирные линии. Всюду Z(0) = 1,^(0) = й .

• •    Обычно используемые в стандартной космологии постоянные решения Ф = Const соответствуют устойчивым особым точкам (притягивающим фокусам). Однако, при небольшом конечном отклонении от особой точки решение скатывается к неограниченному сжатию.

е Таким образом, можно констатировать, что решения, используемые в стандартных сценариях, составляют малый по сравнению с общим фазовый поток, т.е., вероятность таких решений мала.