Особенности формирования притягивающих многообразий в окрестности стационарных траекторий попутного фрезерования концевыми фрезами

Введение. В последние два десятилетия при изучении свойств эволюции и самоорганизации широко используется синергетическая парадигма [1–4]. Ее применение для управления сложными нелинейными объектами нашло свое отражение в работах [5–8]. При создании систем управления динамической системой резания также используются основы синергетической теории управления [7–14]. В этом случае управление, в том числе на основе построения программы ЧПУ, включает определение желаемых траекторий формообразующих движений и соответствующих им

^∗ Работа выполнена по гранту РФФИ №14-08-00206а.

^∗∗∗ The research is done on RFFI grant no. 14-08-00206а.

траекторий движения исполнительных элементов станка. При решении этой задачи принципиально важно знать свойства тех притягивающих множеств, которые самостоятельно образуются в окрестности формообразующих движений инструмента относительно обрабатываемой детали. Необходимо также уметь управлять этими множествами, влияющими на качество поверхности, формируемой при резании. Наконец, раскрытие свойств притягивающих множеств, формирующих сигнал виброакустической эмиссии, открывает новые пути построения информационных моделей для диагностирования процесса [15].

Изучение притягивающих множеств связано с рассмотрением динамической системы резания, изучению которой посвящено множество известных исследований [16-32]. Фрезерование является наиболее сложным процессом резания [33-46]. Это обусловлено его нестационарностью. Параметры длины и толщины срезаемого слоя каждым режущим лезвием периодически изменяются. Поэтому в подвижной системе координат, движение которой определяется траекториями исполнительных элементов, стационарным, установившимся состоянием является не точка равновесия (как при точении), а замкнутая траектория. В связи с этим уравнение динамики имеет периодически изменяющиеся коэффициенты.

Рассмотрим процесс фрезерования на станках, имеющих до пяти координат управления при обработке деталей, параметры жесткости которых существенно изменяются вдоль траектории движения инструмента [44–46]. В настоящей статье, в отличие от известных исследований, учитываются несколько источников самовозбуждения и связи, обусловленные взаимодействиями передней и задней поверхностей инструмента с деталью. Здесь можно рассматривать два случая. Первый — обработка с малыми частотами вращения шпинделя, когда в системе в пределах импульсной реакции параметры можно считать замороженными. Второй — обработка с большими частотами вращения, когда параметры нельзя считать замороженными.

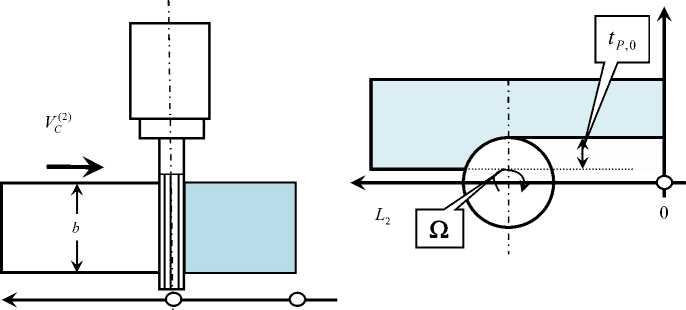
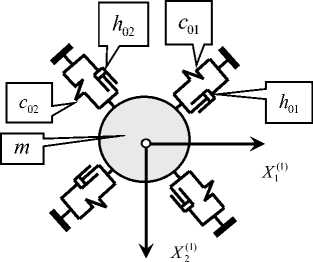
Математическая модель. Рассмотрим попутное фрезерование боковыми лезвиями прямозубой концевой фрезой недеформируемой заготовки (рис.1).

L,                    L 2 ⁽ i )             0

а )

Сечение А - А¹

б )

г )

в )

д )

Рис. 1. Схема взаимодействия подсистем инструмента и обрабатываемой заготовки: деформации при движении стола

е )

в направлении образующей L ₂ (а ), ( б ); деформационные смещения в подвижной системе координат ( в ), ( г ); силы резания в координатах состояния ( д ); учет матриц инерционных, диссипативных и упругих коэффициентов подсистемы инструмента ( е )

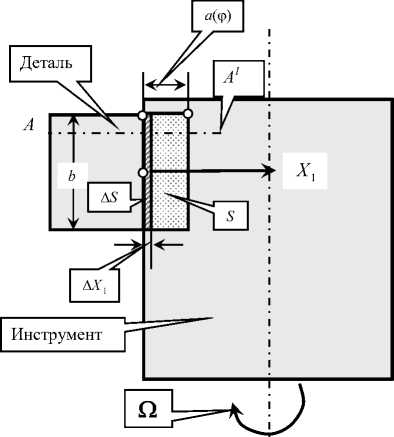
Деформации рассматриваются в плоскости, нормальной к оси инструмента. Считается, что ширина b обрабатываемой заготовки постоянна, то есть b = const . Толщина срезаемого слоя определяется а ( ф ) = а к ( ф ) - X ₁( ф ). Здесь а к ( ф ) — кинематическая составляющая толщины, зависящая от угла ф поворота фрезы. Она не учитывает упругие деформационные смещения инструмента и является периодической функцией угла.

Введем в рассмотрение понятие стационарной траектории деформационных смещений X ² ( ф ) = { X f ( ф ), X f ( ф )} ^Т . Она характеризует установившиеся упругие деформационные смещения инструмента и является периодической функцией ф с тем же периодом. Если в системе сформировалась стационарная траектория, то для нее справедливо: а ( ф ) = а ( ф- i Аф ), a k ( ф ) = a k ( ф - i Аф ), X ² ( ф ) = X ² ( ф- i Аф ), i = 0,1,2,... Рассматривается случай

t

Q = const , где Q — циклическая частота вращения фрезы. Тогда ф = |О dt = Q t . Следовательно, справедливо: о

а ( t ) = а ( t - iT ), а_к ( t ) = а_к ( t - iT ), X ² ( t ) = X ² ( t - iT ), i = 0,1,2...

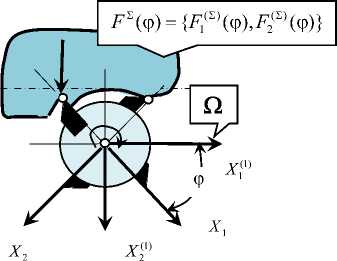
Рассмотрим две системы координат. Первая имеет начало координат в центре фрезы без учета упругих деформационных смещений. В этой системе X ⁽¹⁾ = { X ⁽¹⁾ , X ⁽¹⁾ } T сХ ¹'¹¹ рассматриваются деформации центра фрезы. В частности, при продольном фрезеровании система движется по направлению L^ со скоростью V ⁽²⁾ (рис. 1). В общем случае траектория центра вращения фрезы без учета ее упругих деформационных смещений определяется двумя фазовыми траекториями ( V ⁽¹⁾ = dL 1 / dt , Д) и ( V ⁽²⁾ = dL ₂ / dt , L 2 ). Это программа ЧПУ станка.

Вторая система привязана к кинематической траектории движения вершины режущего лезвия. В данной системе рассматриваются деформационные смещения вершины режущего лезвия X = { X 1 , X ₂ } T с К . Связь между К и К⁽¹⁾ определяется

X(1) = 5(1) X , X = SX(1),                                               (1)

где sin ф

- cos ф

cos φ sin φ

, S =

sin ф cos ф

- cos ф sinφ

Так как Q = const , то операторы S ( Q t ) и S ⁽¹⁾ ( Q t ) есть периодические функции времени. При рассмотрении системы в пространстве К фрезерование имеет свойства, аналогичные точению, но обработка ведется с периодически изменяющейся толщиной срезаемого слоя. Пусть в этом пространстве заданы силы, действующие на режущее лезвие. Тогда в пространстве К

d2 X  ,dX       2/Л

m —— + h--+ cX = FL (t),

dt ²       dt            '”

где m =

m

01         h i

, h = 2

m J       L hi,2

h2,1    c _ cF h2,2 j        _c1,2

c 2,1

c 2,2

— матрицы инерционных, диссипативных и упругих коэффициен

тов инструмента; F ² ( t ) = { F ^{( 2 )} ( t ), F ₂ ²⁾ ( t )} T .

Параметры m , h и c можно определить по правилам, изложенным, например, в [7, 8, 47-49].

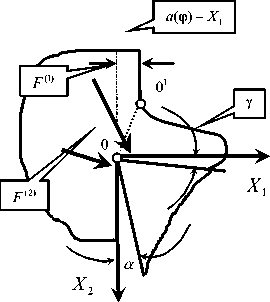
При полной симметрии инструмента матрицы h , с не только симметричные, но и диагональные [50]. Кроме того, они имеют равные коэффициенты и не изменяются при переходе от пространства К к К⁽¹⁾ . Использование синергетического подхода требует выяснения законов взаимодействия системы со средой [3-7] (в нашем случае — с процессом резания). Поэтому необходимо силы резания представить в координатах состояния. Они определяются суммой сил F ² = F ⁽¹⁾ + F ⁽²⁾ (рис. 1).

Следуя [7, 8, 47-49], можно утверждать:

• —    силы возрастают при увеличении площади срезаемого слоя;

• —    имеет место запаздывание между изменениями площади и вариациями сил;

• —    при увеличении скорости резания наблюдается уменьшение сил, которое в скоростном диапазоне (40-180) м/мин можно считать экспоненциальным.

Сила F ⁽²⁾ резко увеличивается при увеличении скорости движения инструмента в сторону заготовки. Зависимость этой силы от колебательной скорости характеризует нелинейное демпфирование. Кроме этого используется гипотеза о неизменности ориентации сил в установившемся состоянии. Она определяется для силы F ⁽¹⁾ угловыми коэффициентами X 1 и х ₂ ■ Для силы F ⁽²⁾ — х⁽¹⁾ и х® ■ Этим свойствам соответствуют следующие представления сил F ² ( t ) = { F 1 ^{( 2 )} ( t ), F^(t )} T .

F 1 ^{( 2 )} ( X 1 , X 2 ) = X 1 P 0 [1 + 0 exp( -a 1 (V - —))] ■ b ■ [ a , ( t ) - Y ] + x ( ¹⁾ F ⁽⁰⁾ ■ exp[ -a 2 dX 1 / dt ]; ^dt

F 2 ^{( 2 )} ( X 1 , X 2 ) = X 2 P 0 [1 + 0 exp( -a 1 ( V - ^f² ))] ■ b ■ [ a , ( t ) - K J + х 21) F ⁽⁰⁾ ■ exp[ -a 2 dX 1 / dt ]; dt

• T dY + Y = X 1 ;

dt

• T dY2₊Y -X

I                                 T2 "dT+Y2 = X1, где T , T — постоянные времени, моделирующие запаздывание сил по отношению к смещениям, с, причем T)T (таким образом учитывается фазовый сдвиг между вариациями сил в направлениях X1, X2 ); р0 — давление стружки на переднюю грань инструмента, кг/мм2; F(0) — сила, действующая на заднюю грань в состоянии равновесия, кг; a1, a2 — параметры, определяющие крутизну изменения сил, с/мм; V — скорость резания.

Модель (3), дополненная (4), описывает динамику фрезерования.

Здесь обработка ведется без перекрытия контактов зубьями фрезы.

Бифуркации динамической системы при отсутствии параметрического самовозбуждения. При малой скорости резания изменениями параметров системы (3) с учетом (4) в пределах импульсной реакции можно пренебречь и рассматривать систему с замороженными коэффициентами [51]. В этом случае необходимо анализировать свойства системы для а , е ( а ⁽¹⁾ , а ⁽²⁾ ) [52-59], то есть при постоянных параметрах на этом отрезке. Рассматриваемая система моделирует два взаимосвязанных колебательных контура, которые имеют два источника самовозбуждения. Один обусловлен запаздыванием сил, второй вызван существованием участка, в котором увеличению скорости соответствует уменьшение сил. Поэтому в зависимости от параметров могут существовать три притягивающих множества: точка равновесия, предельный цикл, двумерный инвариантный тор.

Рассмотрим систему, параметры которой приведены в табл. 1.

Таблица 1

Параметры динамической модели инструмента

т , кг·с2/мм	h , кг·с/мм	c , кг/мм
[ 0,98 - 10 -3        0     1	[ 12   0,0 1	[ 500  0,0 1
0       0,98 - 10 -3	[ 0,0  12 ]	[ 0,0  500 _|

Рассмотрим процесс продольного попутного фрезерования стали 20Х. Основные геометрические параметры инструмента: у = 6 ⁰ , а = 20 ⁰ . Частота собственных колебаний инструмента без динамической связи, формируемой процессом резания: ю₀ = 710,0 Гц . Частоты системы с учетом динамической связи, формируемой процессом резания: ю® = 1540 Гц , го® = 840 ГЦ .

Образование двух частот обусловлено тем, что за счет реакции со стороны резания, матрицы упругости становятся, во-первых, несимметричными, во- вторых, не диагональными.

Давление стружки на переднюю поверхность инструмента — р₀ = (45,0 - 60,0) кг / мм ² .

Коэффициенты ориентации силы: х 1 = 0,6 , х ₂ = 0,8, х⁽¹⁾ = 1, х⁽¹⁾ = 0. Они удовлетворяют условиям нормировки — например, ( X i ) ² + ( х ₂) ² = 1 . Чтобы варьировать основные параметры динамической характеристики процесса резания, изменялись технологические режимы: — скорость резания в пределах 30–110 м/мин;

• —    ширина срезаемого слоя в пределах 5,0–20,0 мм.

Величина подачи на зуб неизменна и равна 0,1 мм/об. Проанализируем диаграмму (рис. 2) в плоскости параметров T 1 - р .

100             300             500    р , кг / мм

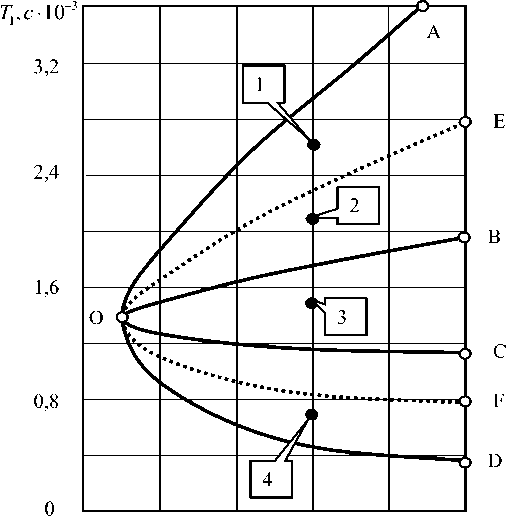
Рис. 2. Бифуркационная диаграмма в плоскости ( T , р ) : A — O — D — область устойчивости равновесия;

В — О — С — область формирования двумерного инвариантного тора; А — О — В — область формирования орбитально-асимптотически устойчивого предельного цикла на низкой частоте; С — О — D — область формирования орбитально-асимптотически устойчивого предельного цикла на высокой частоте

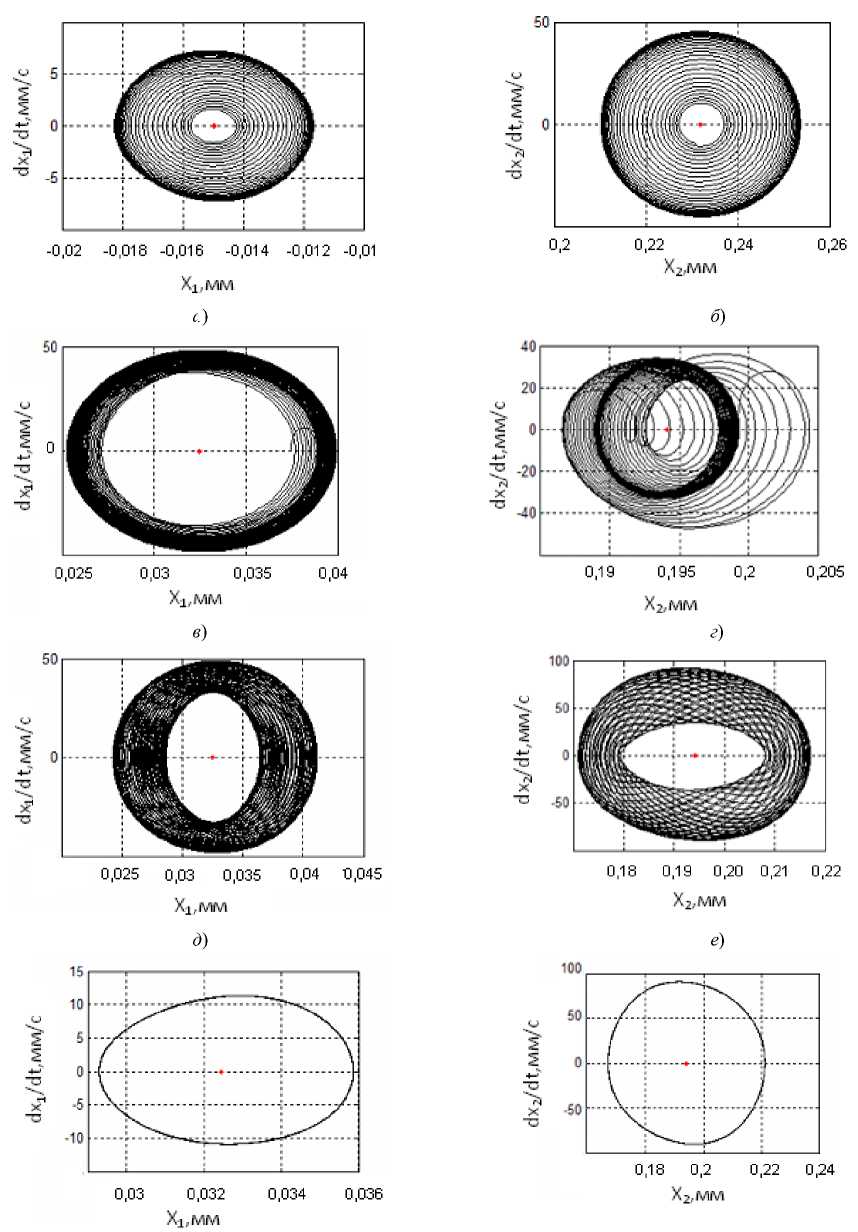
Здесь принято T1 = 0,5T2. Для точек 1, 2, 3, 4 на рис. 3 приведены фазовые траектории в сечениях фазового пространства.

а )

ж )

з )

Рис. 3. Фазовые траектории системы, соответствующие точкам 1 ( а ), ( б) ; 2 ( в ), ( г ); 3 ( д ), ( е ); 4 ( ж ), ( з ) на рис. 2

Все фазовые траектории сверху вниз соответствуют точкам 1, 2, 3, 4 на рис. 2. Кроме того, на рис. 2 приведены также области D-разбиения для линеаризованного в окрестности равновесия уравнения. Они показаны пунктирными кривыми. На участках A — O — D пунктирные кривые совпадают с границами бифуркационной диаграммы, поэтому они сливаются с границами областей D- разбиения. Они определяют четыре области:

• —    область, в которой все корни характеристического полинома линеаризованной системы расположены в отрицательной комплексной полуплоскости А — О — D;

• —    области, в которых пара комплексно сопряженных корней расположена в правой комплексной полуплоскости А — О — Е и F — O — D;

• —    область, в которой две пары комплексно сопряженных корней расположены в правой комплексной полуплоскости Е — О — F ( рис. 2).

Как видно (рис. 2), границы областей D-разбиения не совпадают с границами бифуркаций притягивающих множеств в параметрическом пространстве. Для объяснения этого можно рассмотреть фазовые траектории (рис. 3), соответствующие точкам 1, 2, 3, 4. Временные диаграммы для точки 2 приведены на рис. 4.

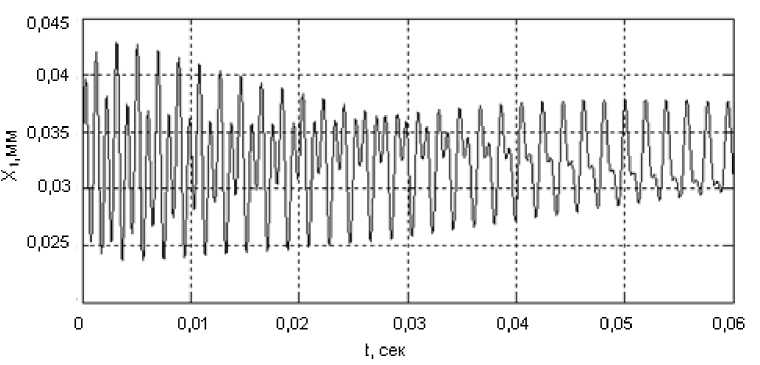
Рис. 4. Пример преобразования двухчастотного процесса в одночастотный, то есть в орбитально-асимптотически устойчивый предельный цикл

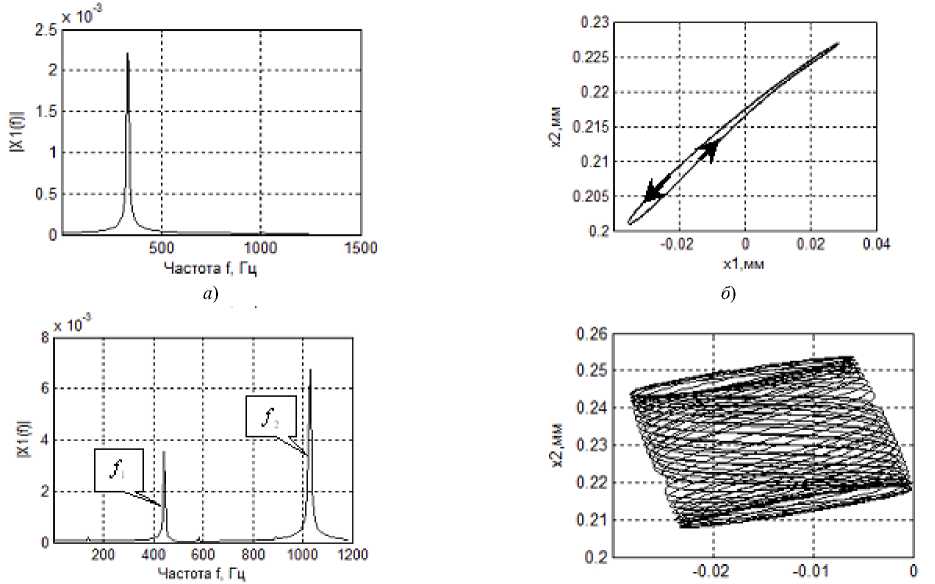
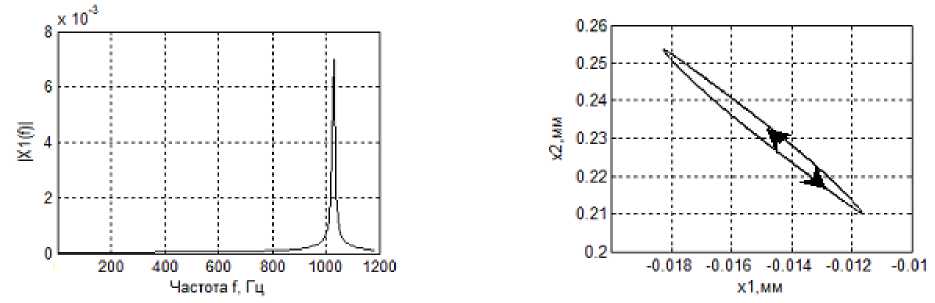
Здесь видно, что двухчастотный процесс со временем преобразуется в одночастотный, то есть имеет место затягивание высокочастотных колебаний к низкочастотным. Аналогичная ситуация возникает и в области С — О — F. Однако здесь низкочастотный процесс стягивается к высокочастотному. Эти эффекты связаны с нелинейной диссипацией, которая учитывается дополнительной связью, формируемой в области контакта задней грани инструмента с заготовкой. Они определяются силой F(2)(dXY / dt) = F(0) • exp[-a2dX^ I dt]{x(1), Хг)}7 ■ Приведем также спектральные характеристики колебаний (рис. 5) в направлении X1 для точек 2, 3, 4 (левые иллюстрации), а также траектории уста новившихся колебаний в плоскости X1 - X2 (правые иллюстрации).

в )

г )

д )

е )

Рис. 5. Изменение спектров установившихся колебаний и их ориентация в плоскости X i — X 2

для точек 2 ( а ), ( б); 3 ( в ), ( г ); 4 ( д ), ( е ) на рис. 2

Анализ влияния упруго-диссипативных параметров подсистемы инструмента на формируемые многообразия показывает: качественно бифуркационная диаграмма соответствует рис. 2. Варьирование c и параметров динамической характеристики процесса приводит к смещениям корней характеристического полинома в комплексной плоскости. При этом корни могут сближаться. В этом случае область, в которой формируется двумерный инвариантный тор, вырождается. Таким образом, при изменении параметров упругости и диссипации подсистемы инструмента происходят изменения притягивающих множеств системы. В наших исследованиях образование хаотических аттракторов для рассматриваемой системы не обнаружено. Типичными притягивающими множествами в системе являются предельные циклы, в редких случаях — инвариантные торы.

Ситуация принципиально меняется, если в системе дополнительно существует параметрическое самовозбуждение.

Влияние параметрического самовозбуждения. По мере увеличения частоты вращения инструмента наступает момент, когда время периодического изменения коэффициентов становится соизмеримым с импульсной реакцией системы. На практике такие условия соответствуют скоростному фрезерованию. К аналогичному эффекту приводит и уменьшение изгибной жесткости инструмента. В этом случае в системе (3), (4) дополнительно образуется источник самовозбуждения, обусловленного периодическими изменениями параметров в динамической связи. Рассмотрим систему, параметры которой без периодической составляющей соответствуют точке 1 на рис. 2. В этом случае без периодического изменения параметров в окрестности единственного равновесия системы формируется притягивающее множество типа предельного цикла на частоте, близкой к Q 0 = 300 Гц . За счет параметрического самовозбуждения образуется дополнительный механизм потери устойчивости. Тогда в колебаниях становится заметным взаимодействие параметрических колебаний и автоколебаний.

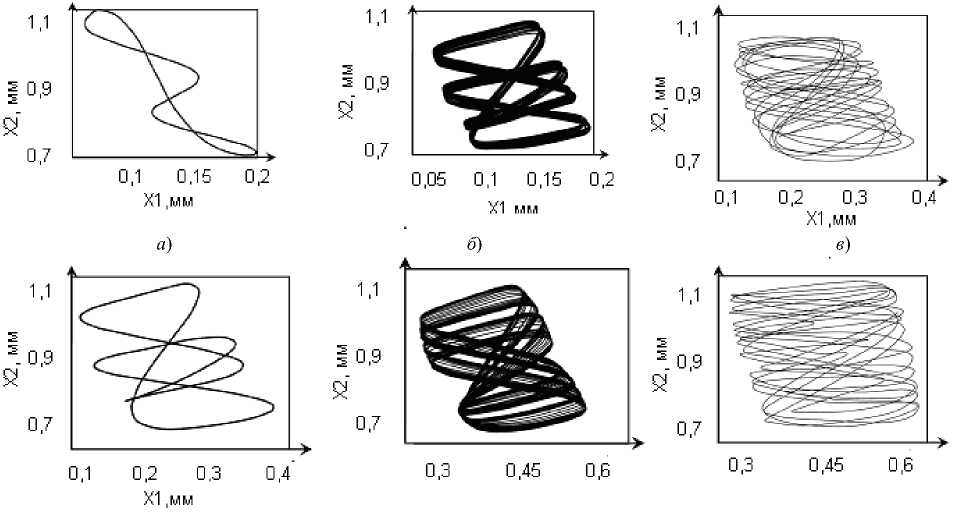
Моделирование стационарных траекторий, иллюстрирующее это взаимодействие, приведено на рис. 6.

г )                                              д )                                                       е )

ж )

з )

Рис. 6. Притягивающие множества в окрестности равновесия по мере увеличения частоты периодического изменения параметров: Q = 150 Гц ( а ); Q = 180 Гц ( б ); П = 210 Гц ( в ); П = 230 Гц ( г ); П = 260 Гц ( д );

( е ); Q = 300 Гц ( ж ); Q = 320 Гц ( з )

На данной иллюстрации показано изменение колебательных смещений инструмента в плоскости, нормальной к оси инструмента. Как видно, по мере увеличения частоты изменения параметров наблюдается синхронизация, в том числе дробного порядка, автоколебаний с периодическими движениями, генерируемыми переменностью параметров в уравнении (3) с учетом (4).

При определенных частотах, зависящих от отношения частоты периодического изменения параметров и собственных частот линеаризованной системы, образуются стационарные траектории типа инвариантного тора (рис. 6, а , ж ).

Образуется также стационарная траектория, которая фактически состоит из двух чередующихся торов (рис. 6, г ).

При переходе от одного детерминированного стационарного состояния к другому наблюдается вначале размытие траекторий ( рис. 6, б , д , з ), а затем образование хаотических колебаний (рис. 6, в , е ).

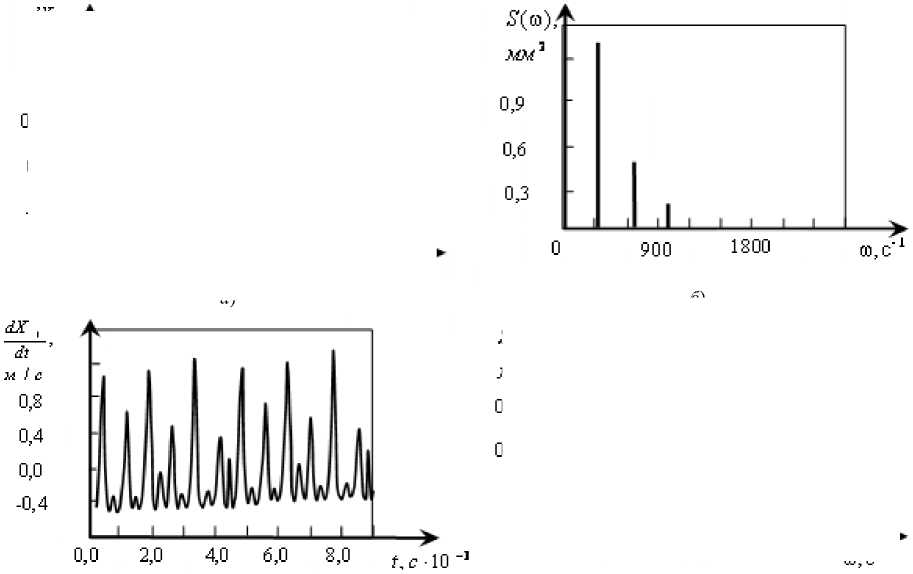
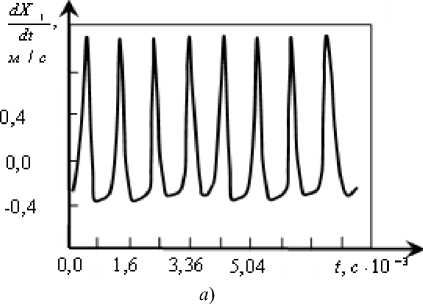
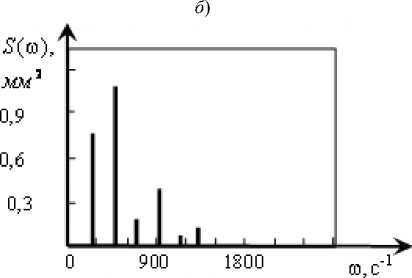
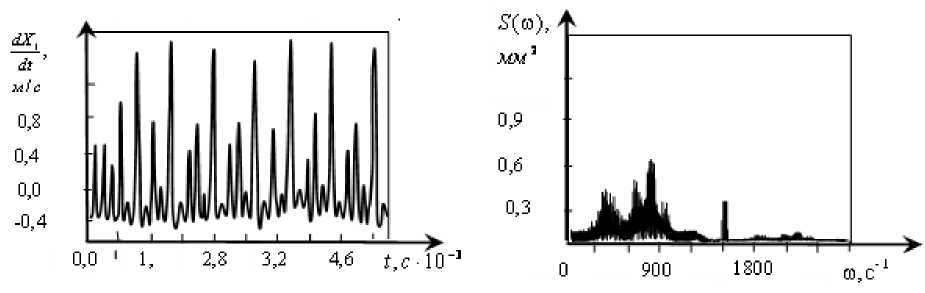
Характерно, что переход к хаотическим колебаниям осуществляется через бифуркации удвоения периода по сценарию М. Фейгенбаума [60]. Для этого проанализируем временные и спектральные характеристики движений инструмента (рис. 7).

в )

г )

д )

е )

Рис. 7. Временные и спектральные характеристики колебательной скорости в направлении X1, соответствующие рис. 6 (а), (б), (в)

На приведенных иллюстрациях видны изменения спектральных свойств колебаний и образование через удвоение периода хаотических аттракторов.

Обсуждение результатов. Фрезерование концевыми фрезами, как правило, сопровождается образованием различных притягивающих множеств, влияющих на процесс обработки и формируемую резанием поверхность. Как показано выше, в зависимости от параметров взаимодействующих подсистем, технологических режимов и геометрии инструмента возможно образование притягивающих множеств типа предельных циклов, инвариантных торов и хаотических аттракторов. Поэтому при управлении процессом фрезерования необходимо не только обеспечивать требуемые траектории движения исполнительных элементов станка, но и заданные свойства системы, которые характеризуются типом притягивающего множества.

Известно, что, например, интенсивность изнашивания инструмента зависит от параметров его автоколебаний [7, 8]. Имеются данные о том, что возбуждение колебаний в зоне резания в отдельных случаях вызывает уменьшение интенсивности изнашивания инструмента, в других — приводит к повышенному износу. Известно также, что интенсивность изнашивания зависит от мощности необратимых преобразований подводимой от станка энергии в зоне обработки. Повышение мощности необратимых преобразований всегда увеличивает интенсивность изнашивания.

Если рассматривать динамическую структуру процесса фрезерования, то необходимо выделить те силы, которые характеризуют необратимые преобразования. Во-первых, это диссипативные силы, которые формируются симметричной составляющей матрицы скоростных коэффициентов. Кососимметричные составляющие, характеризующие гироскопические силы, на виртуальных перемещениях работу не совершают. Поэтому в матрице скоростных коэффициентов работу совершают силы, формируемые симметричной составляющей матрицы скоростных коэффициентов. Кроме этого в матрице упругости работу совершают циркуляционные силы, которые определяются кососимметричной составляющей матрицы упругости. Таким образом, при анализе влияния колебаний на интенсивность изнашивания необходимо рассматривать сумму сил, формируемых симметричной составляющей матрицы скоростных коэффициентов и кососимметричной составляющей матрицы упругости. Именно перераспределение этих сил в нелинейной системе может характеризовать уменьшение мощности необратимых преобразований в зоне резания. Этим, на наш взгляд, объясняется существование периодических траекторий движения инструмента, для которых возможно уменьшение суммарного значение мощности при определенных амплитудах и пространственной ориентации колебаний. Следует отметить, что в зависимости от частоты имеет место оптимальное значение автоколебаний, при которых стойкость максимальна.

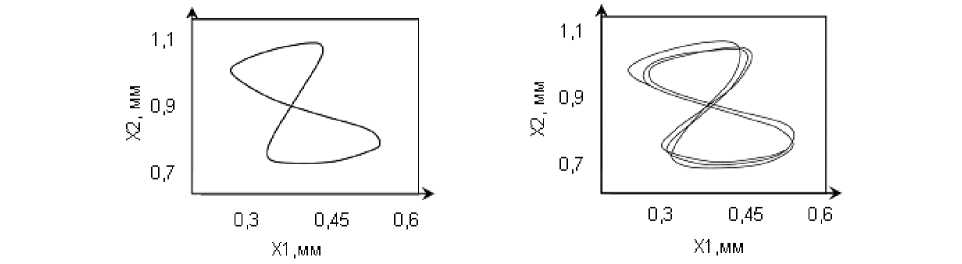
Колебания оказывают противоречивое влияние на формируемую при резании поверхность. Здесь принципиальное значение имеет ориентация колебаний в пространстве. На рис. 8 приведен пример изменения ориентации колебаний для рассмотренной выше системы в зависимости от частоты.

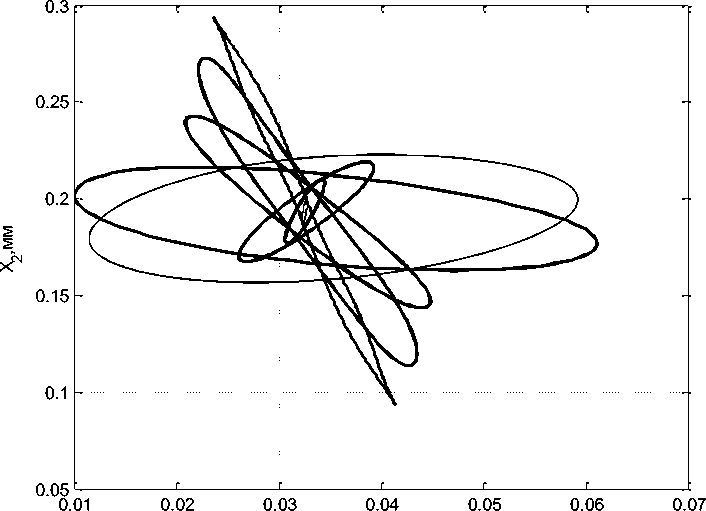
X ,мм

Рис. 8. Изменение ориентации колебаний инструмента в плоскости в зависимости от частоты возбуждения колебаний

Здесь в зависимости от ориентации автоколебаний в пространстве они могут приводить к уменьшению величины шероховатости формируемой поверхности. Колебания ограниченной амплитуды в направлении образующей формируемой поверхности могут существенно улучшать показатели качества формируемой поверхности. Образование автоколебаний в направлении образующей всегда ухудшают шероховатость поверхности.

Наконец, все нелинейные функции в математической модели не являются симметричными в вариациях относительно точки равновесия. Поэтому колебания вызывают смещение точки равновесия системы за счет образования динамического смещения. Это один из механизмов влияния колебаний на геометрический размер формируемой детали.

Заключение. При управлении процессами обработки на станках необходимо решать две проблемы. Первая связана с проектированием траекторий движения исполнительных элементов станков и обеспечением их асимптотической устойчивости. Вторая — с обеспечением заданных свойств траекторий, которые характеризуются типом и параметрами притягивающих множеств, формируемых в окрестностях этих траекторий. Для управления типом формируемых притягивающих множеств необходимо не только изменять технологические режимы, но и выбирать соответствующие параметры динамической структуры процесса — например, геометрические параметры инструментов.