Особенности формирования пространственной избирательности многоканальной многочастотной линейной антенной решетки при регулярном распределении частот по ее элементам

Общей тенденцией развития радиолокационных систем является переход к многоканальным системам с целью повышения объема и качества получаемой радиолокационной информации [1]. В зарубежных изданиях многоканальные радиолокационные системы принято называть MIMO1 РЛС. Отдельным классом MIMO РЛС являются РЛС с многоканальными антенными решетками (АР) [1] с совместной апостериорной обработкой результатов измерений (САОРИ) [2]. Такие РЛС – это новое и перспективное направление в радиолокации [1; 2]. Одним из вариантов реализации MIMO РЛС САОРИ с неразнесенной антенной является использование многоканальной многочастотной линейной АР. Исследованию пространственной избирательности таких систем посвящены работы [3] и [4]. Полученные в указанных работах результаты позволяют установить общие закономерности формирования пространственной избирательности многочастотной АР. Однако свойства функции пространственной избирательности (ФПИ) [5] многочастотной АР с регулярным расположением узкополосных приемо-передающих элементов (далее – эквидистантной) применительно к наиболее важному с практической точки зрения случаю дальней зоны в этих работах изучены недостаточно.

Целью работы является исследование закономерностей формирования ФПИ линейной эквидистантной многоканальной многочастотной АР. Особенность задачи состоит в том, что аналитический анализ полученных общих достаточно громоздких выражений [4], описывающих ФПИ многочастотной АР, как в дальней зоне, так и в зоне Френеля, затруднителен, а результаты математического моделирования столь многообразны, что по ним невозможно установить какую-либо закономерность проявления пространственной избирательности таких АР. Поэтому в работе введены ограничения на размеры АР и приведен случай дальней зоны облучения и приема.

Рассмотрим линейную АР, расстояние между элементами которой равно d (рис. 1). Каждый элемент изотропно излучает и принимает непрерывные гармонические сигналы на своей фиксированной длине волны X n , n = 1.. N , N — число элементов решетки. Для определенности положим, что X n - i <  X n . Элементы решетки расположены на полярной оси. Первый элемент решетки находится в начале полярной системы координат.

Сигналы U_n , излучаемые элементами АР, можно записать в виде

U n = Re { A n exp( ik n R n )exp( i ^ю n t ) } , (1) где k_n = 2п / X _n — волновое число; A n — амплитуда; R_n – расстояние до точки наблюдения; t — время; to _n = c / X _n .

Согласно [3] и [4], многоканальную многочастотную АР апостериори можно сфокусировать в заданную область пространства. Такая фокусировка достигается когерентным весовым суммированием излученных сигналов U_n [4]. Для анализа ФПИ, формирующейся при таком фокусировании, запишем уравнения, описывающее линии равных фаз сигнала, излучаемого n -м элементом АР в фиксированный момент времени t = 0. В случае изотропных приемопередающих элементов линии равных фаз в фиксированный момент времени представляют собой окружности с центром в точке расположения элемента АР и радиусами R_n . В полярной системе координат такие уравнения можно записать так:

р² - 2р nd cos^) + ( nd )² = const = R_n ² , (2) где р и ф — полярные координаты, n = 0.. N - 1. Рассмотрим случай, когда АР сфокусирована в точке P ( F , ф) при условии F >>  d , F >>  X n , F >  2( dN )² /Xq . Тогда, согласно теореме косинусов (см. рис. 1), с учетом разложения подкоренного выражения в ряд Тейлора (пренебрегая величинами ~ 1/ F ²) получим:

R_n = F F ² + ( nd )² - 2 Fnd ео$(ф) + m X _n «

« F - nd cos(y) + m X _n ,

где m — целое число. Слагаемое m X _n учитывает, что при фокусировке АР в точке P ( F , ф) линии равных фаз для каждого элемента АР представляют собой окружности, радиусы которых отличаются на целое число длин волн. Подставляя (3) в (2), получим:

р² - ? ² - 2 nd ( р cos(ф) - ? cos(ф) ) -

₂                      (4)

- 2 m X _n ( F - nd cos(ф) ) + ( m X _n )² = 0.

Перепишем (4) с учетом F >> d :

nd р cos(ф)

р « F +           - cos(ф) + mXn .             (5)

F

После преобразований окончательно получаем уравнение вида

l

р = 1             ’

1 - e cos(ф)

где l = F - cos(ф) - m X _n , e = nd / F . Как известно, это уравнение задает каноническое сечение, фокусы которого находятся на полярной оси, причем один из них совпадает с началом полярной системы координат [6]. Так как в рассматриваемом случае nd / F < 1, то данное уравнение определяет эллипс с фокальным параметром l . Для нахождения максимума ФПИ необходимо ре-

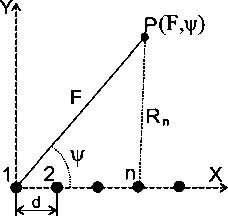
Рис. 1. Геометрия задачи

шить систему уравнений (6). Решения такой системы — точки пересечения эллипсов. При m = 0 (6) имеет два решения (ф = ф, р = F) и (ф = -ф, р = F), первое из которых определяет точку фокусировки АР, а второе является следствием изотропной направленности элементов АР и определяет второй зеркальный (относительно полярной оси) фокус АР. Однако т. к. предполагается, что элементы АР излучают непре- рывные сигналы, которые существуют во всем пространстве, то в общем случае m ^ 0. Далее условимся, что ф е (0, л), и рассмотрим частные случаи.

Случай многоканальной², но одночастотной АР X _n = X q , n = 0.. N -1 при ф = 90°, тогда получим систему уравнений:

F - m X _q ^р 1 nd , . , 1 - -F - сов(ф)

n = 1.. N .

Такая система имеет решение ф = 90° и р = F - mXq, m — целое число. Это решение описывает закономерность формирования ФПИ многоканальной одночастотной АР САОРИ, которая представляет собой максимумы интенсивности, отстоящие друг от друга на расстояние Xq вдоль направления фокусировки. Такая ФПИ позволяет определить направление и дальность до объекта. Однако дальность определяется с неприемлемой неоднозначностью, и можно считать, что в этом случае ФПИ многоканальной одночастотной АР с САОРИ совпадает с диаграммой направленности узкополосной АР с электронным управлением лучом.

Далее рассмотрим случай, когда X _n = X q + + ( n - 1)AX. Тогда необходимо решить систему уравнений:

р=

F - m (X q + n AX)

nd         ^,

^{1 -} F СО8(ф)

n = 1.. N .

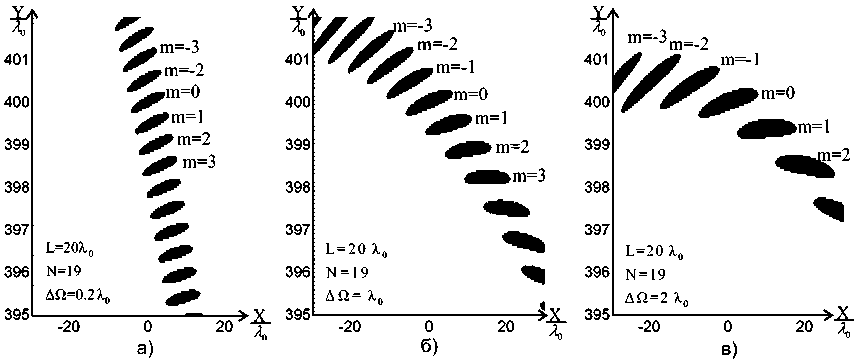
Рис. 2. Сечение ФПИ многочастотной АР на уровне 0.5

Такая система имеет точные решения. Однако удобнее записать их приближенно:

п ф ® —

—

m АХ

и р = F — mХо , d

При m = 0 максимум ФПИ совпадает с точкой фокусирования. В случае m ^ 0 максимумы ФПИ смещены друг относительно друга по углу и дальности. Если учесть, что d = L /( N — 1), L - длина АР, и N АХ = Х n — X q = AQ, можно записать:

ф ®

п

AQ

— m    .

L

Основными параметрами многоканальной АР, определяющими положения максимумов ФПИ в пространстве, являются полоса частот AQ, длина АР L и минимальная длина волны излучения X q . Полученные результаты были проверены методом математического моделирования. На рис. 2 представлены результаты расчета координат максимумов ФПИ для различных параметров АР на математической модели. Сравнения показали, что отклонение величин рассчитанных на

математической модели и согласно полученным выражениям (9) и (10) незначительны.

Для примера в таблице представлены полярные координаты максимумов ФПИ, рассчитанные по (9) и (10) и полученные по результатам математического моделирования.

Заключение

Полученные выражения для расчета пространственных координат максимумов ФПИ линейных многоканальных многочастотных АР в дальней зоне облучения и приема согласуются с результатами проведенного математического моделирования. Результаты исследований показали, что многочастотная АР при регулярном распределении частот по ее элементам обладает многопиковой ФПИ, причем координаты (угловые и по дальности) у каждого максимума различны. Эта особенность позволяет в системах измерения дальности с многоканальной многочастотной АР однозначно определить не только дальность, но и угловое положение объекта локации.

Таблица

Координаты максимумов ФПИ

m	AQ = 0.2 Х 0		AQ =Х 0		AQ = 2 Х 0
	Мат. модель (ф, p/X q )	Расчет (ф, P/X q )	Мат. модель (ф, p/X q )	Расчет (ф, p/X q )	Мат. модель (ф, p/X q )	Расчет (ф, P/X q )
–3	(90,41 ° , 401.52)	(90,40 ° , 401.5)	(92,03 ° , 401.51)	(92,04 ° , 401.5)	(94,05 ° , 400)	(94,09 ° , 401.5)
–2	(90,29 ° , 401)	(90,27 ° , 401)	(90,35 ° , 401.03)	(91,36 ° , 401)	(92,71 ° , 400)	(92,73 ° , 401)
–1	(90,11 ° , 400.51)	(90,13 ° , 400.5)	(90,65 ° , 400.5)	(90,68 ° , 400,5)	(91,35 ° , 400,5)	(91,36 ° , 400,5)
0	(90 ° , 400)	(90 ° , 400)	(90 ° , 400)	(90 ° , 400)	(90 ° , 400)	(90 ° , 400)
1	(89,85 ° , 399.5)	(89,86 ° , 399.5)	(89,3 ° , 399.5)	(89,32 ° , 399.5)	(88,65 ° , 399.49)	(88,64 ° , 399.5)
2	(89,71 ° , 398.98)	(89,72 ° , 399)	(88,63 ° , 400)	(88,64 ° , 399)	(87,25 ° , 400)	(87,27 ° , 399)
3	(89,57 ° , 398.48)	(89,59 ° , 398.5)	(87,95 ° , 400)	(87,95 ° , 398.5)	(85,92 ° , 400)	(85,90 ° , 398.5)