Особенности формирования умений построения доказательства

Традиционный стиль обучения предполагает догматический характер доказательства, ученику в голову не приходит, что доказательства можно проводить по-разному (и в разной последовательности). Ясно, что на уроке (при условии минимума времени на изучение математики) рассмотреть различные способы доказательства многих теорем просто невозможно. Но, все же рекомендуется учителю «выкраивать» время для хотя бы еще одного доказательства теоремы или задачи на доказательство, в том числе и в качестве пропедевтики.

Самое сложное в организации решения задачи разными способами это помощь учителя в нахождении этих способов. При этом учитель должен выступить не с идеей нового варианта доказательства (или разных вариантов), а с вопросом или серией вопросов, инициирующих появление соответствующей идеи или идей. Сложность связана с тем, что эта творческая деятельность учителя направлена не на применение некоторого знания или приёма, а на развитие воображения или интуиции ученика.

Представим некоторые общие условия, способствующие успешному нахождению различных способов доказательства требований задач.

• 1)    Для успешного обучения школьников нахождению различных способов доказательства надо научить их с помощью синтетической деятельности получать необходимые посылки для доказательства предложений.

• 2)    Для обеспечения индивидуального характера этого процесса

необходимо ориентироваться на различные уровни способностей учащихся.

• 3)    Учитель обязан постоянно и умело наблюдать за процессом мышления учащихся, анализировать и изучать его. Это очень важная задача, осуществление которой способствует привитию интереса к предмету.

• 4)    Если учителю удаётся привить учащимся интерес к отысканию различных способов решения задач (доказательств математических предложений), то он сможет практиковать такую работу и в ходе изучения программного материала.

Задача: Диагонали трапеции разбивают ее на четыре треугольника. Докажите, что треугольники, прилежащие к боковым сторонам равновелики.

Для решения этой задачи различными способами можно разбить класс на 34 группы.

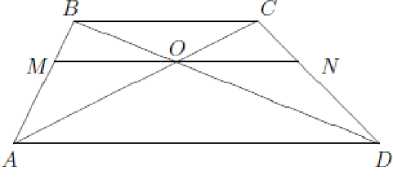
Рис.2

Каждой группе даётся карточка с условием задачи и подсказкой идеи решения. Цель каждой группы выработать стратегию доказательства на основе идеи (идей), предложенной в карточке. В случае затруднения учитель задаёт наводящие вопросы каждой группе. Группа стремится обосновать своё доказательство, используя при этом минимальное количество подсказок. Выдвинув своё доказательство, группа направляет своего представителя к доске. Этот ученик объясняет доказательство. Проверка решения осуществляется в форме беседы. Учащиеся анализируют решение и задают вопросы. Учитель концентрирует внимание учеников на наиболее важных моментах рассуждения.

• 1) Указания первой карточки:

• 2) Указания второй карточки:

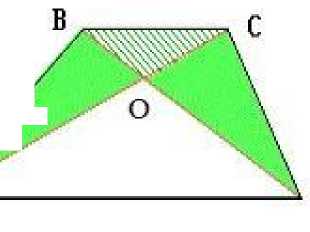
Рис.3

Идея доказательства: прировнять площади искомых фигур

Подсказки первой группе:

• 1)    «Не видите ли вы треугольник, в который включаются Δ AOB и ^ CDO »?

Этой подсказки может быть достаточно для решения задачи.

Если первая подсказка не помогла, то группе предлагаются следующие наводящие вопросы:

• 2)    «Площади, каких фигур включают в себя площадь треугольника ABD »?

• 3)    «Что является пересечением треугольников ABD и ACD »?

И подобные вопросы.

Опираясь на принадлежность одних треугольников другим, учащиеся первой группы выстраивают следующее доказательство самостоятельно или используя приведённые подсказки.

Решение первой группы:

• 1)    Рассмотрим треугольники Δ ABD и Δ ACD . У них общее основание AD и равные высоты, проведённые к этому основанию.

• 2)    Из этого можно сделать следствие:

С - V С - V V

и

• 3)    Площади равны, следовательно, треугольники равновелики. Ч.Т.Д.

Указания второй карточки:

Идея доказательства:

• а)    использовать метод от противного.

• б)    провести через точку O отрезок MN BC .

Подсказки группе .

Подсказку можно дать на часть б) – «Воспользоваться ранее доказанным фактом о том, что OM = ON ».

Способ решения части а):

• 1)    Допустим обратное: S Δ ABO ≠ S Δ COD

• 2)    Тогда, S _{Δ ABD} ≠ S _{Δ ACD} и, следовательно BC не параллельно AD – это приводит к противоречию, что ABCD – трапеция.

• 3)    Значит, предположение неверно и S _{Δ ABO} = S _{Δ COD} . Что и требовалось

доказать.

Способ решения части б):

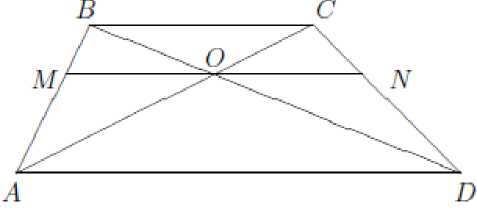
Рис.4

• 1)    Разобьем, рассматриваемые треугольники Δ AOB и Δ COD

на части. Для этого проведем MN II BC , OM = ON .

Получаем, что треугольники  ΔAOB  и  ΔCODсостоят из двух треугольников, площади которых: SΔAMO = SΔDNO , SΔBMO = SΔСNO .

Указания третьей карточки:

Идея доказательства: Вычислить площади треугольников, используя подобие.

Подсказки группе .

По известной формуле: S = ¹ ab ⋅ sin α вычислите площади треугольников

Δ AOB и Δ COD , используя подобие треугольников Δ BOC и Δ COD .

Решение третьей группы

• 1)    Δ BOC ~ Δ COD , тогда ^BO = ^CO и AO ⋅ BO = CO ⋅ DO . DO AO

• 2)    Умножив обе части последнего равенства на ¹ sin α , получаем:

• ¹    AO ⋅ BO ⋅ sin α = ¹ CO ⋅ DO ⋅ sin α , где ∠ α = ∠ AOB = ∠ COD . 22

3)Следовательно, S _{Δ ABO} = S _{Δ COD} . Ч.т.д.

Учащиеся формируются в группы по способностям и умениям. Каждая группа выступает со своим доказательством. Усвоив решение своей группы, ученик способен овладеть другими способами доказательства. В процессе представления доказательства учащийся развивает свою математическую речь, показывает умение рассуждать и отстаивать идеи.

Описанный подход приводит, во-первых, к развитию математического мышления в целом. Во-вторых, исчезают боязнь неуспеха, страх перед задачей, повышается самооценка в данном виде деятельности.