Особенности формирования величины рыночной стоимости недвижимости при логарифмически нормальном распределении цен

При определении рыночной стоимости объектов недвижимости с использованием сравнительного подхода возникают проблемы выбора объектов сравнения, формирования представительной выборки и, собственно, построения оценки рыночной стоимости. Основными трудностями являются доступ к электронным и достаточно обширным базам данных, их недостаточная информативность с точки зрения учета максимально возможного набора ценообразующих факторов и непосредственно статистическая обработка доступных данных. Как правило, в практике оценки выборки не являются представительными, содержат малое количество объектов сравнения. При этом, как справедливо отмечалось в работе [1], проверка статистических гипотез часто не проводится.

Мы используем стохастическую модель ценообразования на рынке жилой недвижимости, основанную на последовательных сравнениях цен. Процесс последовательных сравнений при стандартных предположениях 1 имеет единственный невырожденный предел по распределению для цены – закон логнормального распределения вероятностей. Соответствие эмпирических распределений цен логнормальному закону подтверждаем статистическими данными о рынке недвижимости города Санкт-Петербурга. Для проверки согласия эмпирических распределений теоретической модели в основном используем мощный и чувствительный статистический критерий Колмогорова-Смирнова. Опираясь на федеральный стандарт оценки «Цель оценки и виды стоимости (ФСО № 2)» (далее – ФСО № 2), мы делаем вывод о том, что рекомендуемая наиболее вероятная цена – это мода распределения, которая корректно и однозначно определяется в результате аппроксимации логнормальным законом. Поскольку у логнормального распределения среднее

* Результаты исследований по теме настоящей статьи докладывались на 2-й международной конференции «Математика и компьютеры в науке и промышленности» (MCSI 2015) 17–19 августа 2015 года (Мальта).

превосходит наиболее вероятное значение – моду, оценки рыночной стоимости, опирающиеся на оценку математического ожидания, систематически завышены.

В ФСО № 2 прямо указано, что «При определении рыночной стоимости определяется наиболее вероятная цена, по которой объект оценки может быть отчужден на дату оценки на открытом рынке в условиях конкуренции, когда стороны сделки действуют разумно, располагая всей необходимой информацией, а на величине сделки не отражаются какие-либо чрезвычайные обстоятельства» (в новой редакции ФСО № 2, принятой в 2015 году, есть ссылка на определение рыночной стоимости, закрепленное в Законе № 135-ФЗ). Аналогичные формулировки содержат и зарубежные стандарты оценки (см. [3–6]).

Мы рассматриваем формулировки стандартов оценки как основу для получения численного значения цены. Определения рыночной стоимости, указанные в стандартах, однозначно устанавливают наличие вероятностного фактора, заложенного в природу цены. То есть, цена – случайная величина, а рыночная стоимость – ее числовая характеристика (мода). Распределение вероятностей случайной величины полностью описывается функцией распределения (или плотностью, когда таковая существует). Из определения следует, что для построения оценки рыночной стоимости необходимо иметь теоретическое или эмпирическое распределение и на его основе вычислять наиболее вероятное значение. Стандартный подход в случае эмпирического распределения – построить гистограмму выборки, подобрать удовлетворительную с точки зрения какого-либо критерия кривую плотности распределения, найти точку максимума. В случае наличия стохастической модели теоретического распределения проверяется согласие данных с модельным распределением и в качестве наиболее вероятного значения берется оценка моды теоретического распределения. Подобные подходы обусловлены тем, что эмпирические распределения, задаваемые гистограммами, формально не унимодальны 2.

В случае унимодальных распределений, таким образом, будет получена точечная оценка рыночной стоимости, на необходимость которой указывается в работе [7]. Точность такой оценки во многом будет определена объемом выборки. Интервальные оценки могут быть получены в терминах доверительных интервалов с учетом вида закона распределения. Используемые в оценке методы обработки статистического материала часто ориентированы на нормальное распределение и не всегда применимы к распределениям цен. Одной из особенностей нормального распределения являются его симметричность и равенство моды, математического ожидания и медианы. Между тем существуют теоретические основания и практические подтверждения того, что цены на однородные активы чаще всего не имеют нормального распределения.

Предположение о логнормальности распределений цен непосредственно вытекает из фундаментальной работы [8]. Этот подход отмечен, в частности, и в работе [9] с оговоркой о его сложности с точки зрения математического аппарата. Здесь следует отметить, что возможностей MS Excel (которыми пользуются и авторы работы [9]) недостаточно для статистических исследований. Для этого необходимо использовать специальные статистические пакеты, позволяющие быстро получать требуемые результаты, в том числе в целях оценки. Такие пакеты, например, использованы в работе исследователей центра Японской экономики и бизнеса Колумбийского университета (Нью-Йорк) [10], которые, исследуя статистические данные по Большому Токио, приходят к выводу о том, что при отсутствии сильных внешних возмущений цены подчиняются логарифмически нормальному закону распределения (объем использованных баз данных – 724 416 записей для кондоминиумов и 1 602 918 для отдельных домов). Также необходимо отметить работу итальян- ских исследователей экономического факультета Римского университета [11], которые, исследуя динамику цен во времени, устанавливают ее следование геометрическому броуновскому движению, из чего немедленно вытекает закон логарифмически нормального распределения цен.

В работе [12] нами доказано, что при достаточно простых и естественных предположениях процесс последовательных сравнений цен сходится по распределению к логарифмически нормальному распределению.

Определение логарифмически распределенной случайной величины

Мы говорим, что случайная величина X имеет логнормальное распределение, если она допускает следующее представление:

X = exp[μ + σN(0,1)], где μ – математическое ожидание (нормального) распределения lnX;

exp ( μ ) – медиана распределения X ;

положительный параметр σ > 0 – стандартное отклонение;

σ ² – дисперсия нормального распределения lnX ;

N ( μ , σ ²) – обозначение (условное) как для нормального распределения со средним μ , дисперсией σ ², так и для соответствующей случайной величины.

Из модели логарифмически нормального распределения цен немедленно вытекает ряд существенных особенностей рыночной стоимости:

• 1)    применение средних арифметических для оценки рыночной стоимости (моды) приводит к систематической ошибке оценки в сторону завышения. Поскольку среднее логнормального закона есть exp ( μ + 1/2 σ ²), а мода равна exp ( μ – σ ²), отношение среднего к моде не зависит от μ , всегда больше единицы и равно exp (3/2 σ ²);

• 2)    аналогично применение средних геометрических (оценка медианы) приводит к систематической ошибке в сторону завышения. Отношение медианы к моде не зависит от μ , всегда больше единицы и равно exp ( σ ²);

• 3)    из свойств логнормального распределения следует, что при постоянном μ с ростом σ увеличивается разница между математическим ожиданием, медианой и модой. Таким образом, при постоянном μ и растущем σ среднее арифметическое (оценка математического ожидания exp ( μ + 1/2 σ ²)) растет, а рыночная стоимость (мода exp ( μ – σ ²)) уменьшается. В этом случае отслеживание средних значений может привести к неверным представлениям о состоянии рынка, так как по средним будет наблюдаться восходящий тренд, в то время как рыночная стоимость будет снижаться;

• 4)    при логарифмически нормальном распределении рыночная стоимость не симметрична в том смысле, что вероятность отклонения от рыночной стоимости вниз и вверх неодинакова. Более того, вероятность отклонения вверх всегда выше, чем вероятность отклонения вниз. Используя распространенное для цены обозначение V и полагая, что V допускает представление X = exp [ μ + σ N (0,1)], получаем, что вероятность попадания цены V в интервал от 0 до exp ( μ – σ ²) равна:

P[0 < V < exp(μ – σ2)] = Ф(-σ) < 1/2, дополнительная вероятность попадания в интервал от exp(μ – σ2) до + ∞ равна:

P[exp(μ – σ2) < V < +∞] = 1 – Ф(-σ) > 1/2, где Ф – функция распределения стандартного нормального закона (функция Лапласа плюс 1/2).

Таким образом, тот факт, что зачастую сделки совершаются по цене выше цены, установленной при оценке рыночной стоимости, неудивителен. Это обусловлено асимметрией распределения цен и зависит только от σ (среднеквадратического отклонения распределения логарифмов цен, которое следует рассматривать как характеристику волатильности рынка в текущий момент времени).

Из практики следует, что базы данных по недвижимости содержат неоднородные активы. В этом случае элементы для сравнения мы берем из подвыборок, сформированных по тому или иному принципу однородности. Для каждой такой выборки формируется соответствующее логнормальное распределение со своими параметрами μ , σ ². При этом совокупное распределение формируется путем смешивания (о смеси распределений см. [13]) логнормальных распределений со смешивающими коэффициентами (весами), пропорциональными количеству единиц сравнения в выборке, сформированной по принципу однородности (например по районам, зонам ценовых предпочтений, типам домов, квартир и т. п.).

Определение смеси

Пусть имеется m функций распределения F ₁, ..., F_m – «элементов смеси» и m неотрицательных чисел, называемых «весами», a ₁, ..., а_m , сумма которых равна единице. Тогда функция H , определенная посредством равенства H ( x ) = a ₁ F ₁( x ) + ... + a_mF_m ( x ) , x ∈ R , является функцией распределения, которое называется смесью распределений F ₁ , ..., F_m с соответствующими весами a ₁, ..., a_m .

Если у распределений F ₁, ..., F_m существуют плотности f ₁, ..., f_m , то и у распределения H существует плотность h , равная h ( x ) = a ₁ f ₁( x ) + ... + a_mf_m ( x ), x ∈ R .

Введем случайные величины X ₁, ..., X_m , имеющие соответствующие функции распределения F ₁, ... , F_m , и так называемую «смешивающую» случайную величину ν , принимающую значения 1, ..., m с соответствующими вероятностями a ₁, ..., a_m (числа a по построению естественно трактуются как вероятности). Важно, чтобы случайная величина v не зависела от X ₁, ..., X_m , при этом случайные величины X ₁, ..., X_m могут быть произвольно взаимозависимыми. Тогда смесь реализуется по следующему алгоритму: реализуем сначала ν , а затем X _ν с тем номером, на который указала ν . Полученную в результате такого алгоритма случайную величину обозначим Y . Из формулы полной вероятности следует, что функция распределения Y есть H . Ничего не изменится, если рассматривать счетный набор весов. Говоря языком чистой математики, смесь распределений – это выпуклая аффинная комбинация распределений.

Для практических вычислений важно отметить, что смесь нормальных распределений после потенцирования превращается в смесь логнормальных распределений с теми же весами.

Суть приведенного далее утверждения в том, что если функция распределения случайной величины является смесью нормальных функций распределения, то функция распределения ее экспоненты является смесью логнормальных распределений, и наоборот.

Утверждение

• A.    Пусть функция распределения H случайной величины Y задается в виде H ( x ) = a ₁ F ₁( x ) + ... + a_mF_m ( x ). Причем функции распределения F ₁, ..., F_m являются функциями распределения нормального закона с соответствующими параметрами.

N ( μ_j , σ _j ² ), j = 1, ..., m . Тогда случайная величина exp ( Y ) имеет функцию распределения вида:

a1G1 + ... + amGm, где Gj – функция распределения логнормального закона с параметрами:

μ_j – медиана;

σ _j ² – волатильность;

j = 1, ..., m .

• B.    Пусть распределение случайной величины Z представимо в виде смеси логнормальных распределений с соответствующими параметрами:

μ_j – медиана;

σ _j ² – волатильность;

j = 1, ..., m .

Тогда распределение случайной величины Y = ln ( Z ) является смесью с теми же весами нормальных распределений N ( μ_j , σ _j ² ), j = 1, ..., m .

Несложное доказательство этого утверждения приводится в работе [12].

Задача выделения из смеси распределений ее компонент относится к классу некорректных задач. Для решения таких задач часто используются факты и приемы, относящиеся к предметной области. В случае с недвижимостью – это разбиение общей выборки на естественные зоны, кластеры, районы, типы недвижимости, типы зданий и т. п.

Приведенное утверждение позволяет нам переходить от единичного нормального распределения к смеси нормальных распределений и в конечном итоге – к смеси логнормальных распределений для зон, кластеров, типов домов и других значимых ценообразующих факторов. В этом случае возможность учета тех или иных факторов зависит только от архитектуры баз данных, доступных для исследования. В использованной нами базе данных [14] пригодными для фильтрации (разделения смеси) являются такие факторы, как вид недвижимости, местоположение, тип дома. Содержащуюся в этой базе смесь удалось разделить на компоненты (элитная жилая недвижимость – вторичный рынок – масс-маркет, новое строительство жилой недвижимости – масс-маркет), хорошо описывающиеся логарифмически нормальным законом (приведены далее). Важно отметить, что, несмотря на то, что смесь логнормальных распределений не является логнормальным распределением, когда множество совокупных значений параметров μ и σ ² имеет небольшой разброс, полученное в результате смешивания (теоретическое) распределение может остаться унимодальным (то есть иметь одну моду – одно значение с максимальной вероятностью).

В любом случае, когда значения μ и σ ² в смешивающих распределениях имеют небольшой разброс и смешивающие распределения имеют веса примерно одинакового порядка, итоговое распределение имеет по меньшей мере хорошо выделяемый, узкий интервал «максимальной вероятности».

Рассмотрим пример.

Был изучен статистический материал:

• •    объявления о продажах объектов жилой недвижимости, опубликованные в базе [14];

• •    дата выборки – 27 апреля 2015 года;

• •    размерность цены – тысяча рублей за 1 квадратный метр (скидка на торг не учитывалась – мы считаем ее объектом, достойным самостоятельного исследования);

• •    общая выборка (объем 7 922 объекта) является смесью распределений недвижимости разных классов.

Разделение выборки на вторичный рынок и новое строительство (а внутри этих классов на элитный сектор и масс-маркет) позволило создать соответствующие выборки, хорошо приближающиеся логнормальным законом. Теоретические кривые получены методом максимального правдоподобия, затем использовался критерий согласия Колмогорова-Смирнова. При удовлетворении заданному значению p-value > 0,05 не отрицается гипотеза о логнормальности с параметрами μ и σ ² для распределения цены предложения 1 квадратного метра случайно выбранного объекта недвижимости.

После того как распределение прошло тест Колмогорова-Смирнова, наиболее вероятной ценой считается мода (как и предписывается определением рыночной стоимости) логнормального распределения exp ( μ – σ ²).

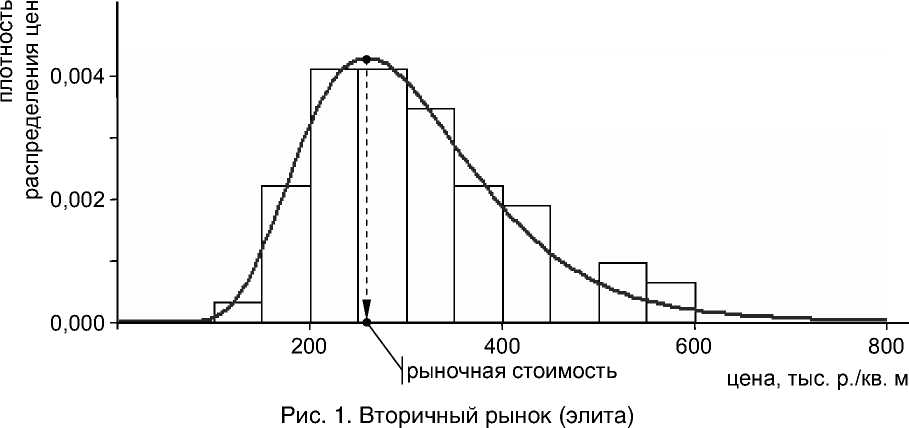
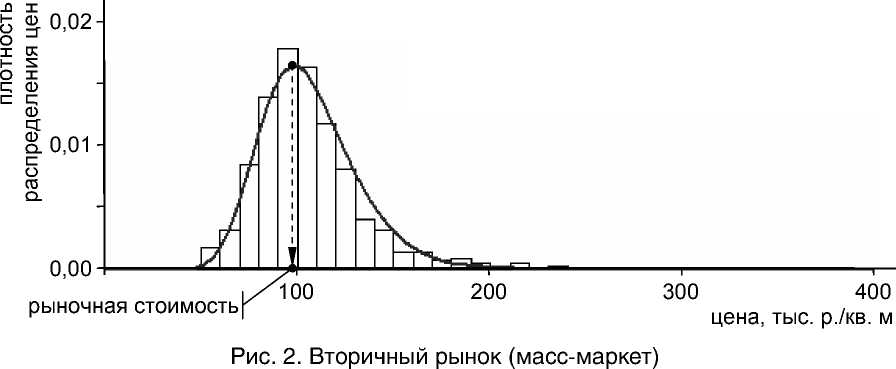
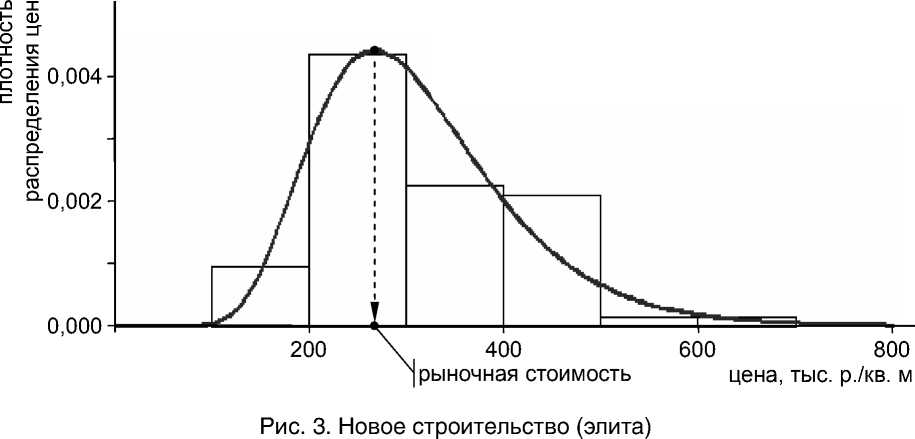
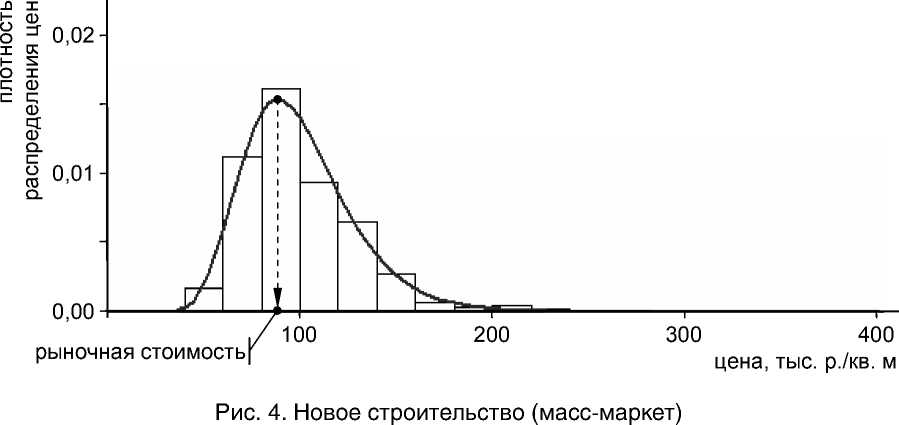
Все расчеты проведены в статистическом пакете R . На рисунках 1–4 представлены гистограммы эмпирической плотности распределения соответствующей случайной величины и кривые плотности логарифмически нормального распределения с параметрами, полученными методом максимума правдоподобия и обеспечивающими удовлетворительное значение теста Колмогорова-Смирнова (далее – КС-тест).

В таблице 1 приведены цифровые параметры логнормального закона распределения, результаты КС-теста, средние значения цен по выборкам и оценки рыночной стоимости недвижимости, полученные для каждой группы объектов.

Таблица 1

Численные результаты обработки данных для рисунков 1–4

Параметр		Вторичный рынок		Новое строительство
		элита (рис. 1)	масс-маркет (рис. 2)	элита (рис. 3)	масс-маркет (рис. 4)
Параметры логнормального закона распределения	μ	5,6699	4,6411	5,6926	4,563
	σ	0,3375	0,2698	0,3212	0,281
Результат КС-теста	D	0,0475	0,0293	0,0896	0,0281
	p-value	0,9989	0,1196	0,7023	0,0781
Оценка рыночной стоимости 1 кв. м, exp ( μ – σ 2), тыс. р.		258,792	96,375	267,579	88,592
Среднее значение цены по выборке, тыс. р./кв. м		306,807	107,813	312,123	101,818

Полученные выборки также удается разделить на компоненты, хорошо приближающиеся логарифмически нормальным законом распределения. Сектор элиты (или премиум-класса) по районам и типам домов не разделялся. Сектор масс-маркета разделен по административным районам (как для нового строительства, так и для вторичного рынка) и типам домов (только на вторичном рынке). С целью экономии места результаты сведены в таблицы 2–4 (в столбцах «отклонение» имеется в виду отклонение (в процентах) средних по выборке от рыночной стоимости).

Таблица 2

Новое строительство (масс-маркет)

Район	μ	σ	Среднее	Мода	Отклонение, %	p-value
Адмиралтейский	4,8000	0,2600	142,646	113,568	25,6	0,24
Василеостровский	4,6000	0,2500	101,597	93,457	8,7	0,12
Выборгский	4,4200	0,2180	88,664	79,240	11,9	0,11
Калининский	4,4619	0,1400	87,673	84,973	3,2	0,13
Кировский	4,6562	0,0753	105,526	104,640	0,8	0,45
Колпинский	4,2008	0,2900	68,200	61,355	11,2	0,57
Кронштадтский	4,3369	0,0810	76,712	75,969	1,0	0,39
Московский	4,7700	0,2200	131,045	112,348	16,6	0,48
Невский	4,4217	0,2299	86,284	78,951	9,3	0,08
Петроградский	4,9900	0,1600	155,572	143,223	8,6	0,11
Приморский	4,7000	0,3220	118,250	99,118	19,3	0,84
Пушкинский	4,3265	0,2491	78,182	71,126	9,9	0,16
Центральный	5,2180	0,3506	196,478	163,219	20,4	0,08
Красногвардейский	4,7500	0,3200	116,717	104,334	11,9	0,07
Красносельский	4,5500	0,1560	95,840	92,357	3,8	0,16
Курортный	4,4624	0,0982	87,108	85,863	1,4	0,65
Петродворцовый	4,1457	0,0471	63,235	63,025	0,3	0,62
Фрунзенский	4,5643	0,0600	96,389	95,648	0,8	0,75

Таблица 3

Вторичный рынок (масс-маркет)

Район	μ	σ	Среднее	Мода	Отклонение, %	p-value
Адмиралтейский	4,6973	0,2865	114,838	101,005	14	0,10
Василеостровский	4,8141	0,2478	127,223	115,897	10	0,62
Выборгский	4,6420	0,1858	105,471	100,235	5	0,17
Калининский	4,6397	0,1604	104,898	100,883	4	0,60
Кировский	4,5889	0,1303	99,226	96,733	3	0,99
Колпинский	4,3177	0,1588	75,962	73,148	4	0,96
Кронштадтский	Нет данных

Окончание таблицы 3

Московский	4,7448	0,1922	117,183	110,811	6	0,34
Невский	4,5739	0,1634	98,228	94,369	4	0,54
Петроградский	4,8607	0,3230	136,166	116,329	17	0,92
Приморский	4,6456	0,2062	106,381	99,794	7	0,96
Пушкинский	4,5407	0,2869	97,971	86,350	13	0,58
Центральный	4,8602	0,3336	137,172	115,460	19	0,09
Красногвардейский	4,5665	0,2079	98,438	92,133	7	0,47
Красносельский	4,4995	0,1749	91,342	87,262	5	0,61
Курортный	4,3732	0,2455	81,696	74,662	9	0,67
Петродворцовый	4,3854	0,1225	80,881	79,075	2	0,98
Фрунзенский	4,5962	0,1311	99,982	97,421	3	0,63

Таблица 4

Вторичный рынок по типам домов

Типы домов	μ	σ	Среднее	Мода	Отклонение, %	p-value
Хрущевки	4,5086	0,1470	91,798	88,851	3	0,88
Брежневки	4,4791	0,1499	89,143	86,196	3	0,82
Панельные дома	4,5275	0,2040	94,459	88,755	6	0,43
Блочные дома	4,5610	0,2255	98,095	90,937	8	0,63
Серии	4,5654	0,1507	97,157	93,940	3	0,46
Старый фонд	4,7200	0,3200	132,719	101,251	31	0,15
Кирпичные дома	4,6300	0,2300	110,020	97,232	13	0,33
Старый фонд с капитальным ремонтом	4,9200	0,4512	157,075	111,769	41	0,08
Сталинские дома	4,7300	0,2700	125,518	105,330	19	0,89
Индивидуальные проекты	4,7864	0,4461	132,861	98,241	35	0,85
Монолитные дома	4,6800	0,3000	117,401	98,494	19	0,32
Реконструкция	5,4886	0,5634	281,481	176,122	60	0,87

Возможно дальнейшее разбиение смесей, однако в изучавшейся базе данных не содержится более обширный набор ценообразующих факторов. В то же время имеющиеся в базе факторы (вид недвижимости, место, тип дома) являются наиболее значимыми, что достаточно для определенного круга аналитических исследований.

Для целей оценки могут быть разработаны дополнительно принципы работы с малыми выборками, кроме того, могут использоваться традиционные методы (например метод парных сравнений), но уже внутри сформированной выборки.

Выводы

• 1.    Рыночная стоимость является числовой характеристикой закона распределения цен.

• 2.    Определенная как мода, рыночная стоимость требует построения закона распределения и нахождения точки максимума плотности распределения.

• 3.    При логарифмически нормальном распределении рыночная стоимость не может быть оценена средними.

• 4.    Многовершинность плотности распределения свидетельствует о наличии неоднородных активов в выборке. Такая выборка является смесью и нуждается в дальнейшем разделении.

• 5.    При логарифмически нормальном распределении уклонение цены от рыночной стоимости в бо ́ льшую сторону всегда вероятнее, чем в меньшую.

• 6.    При логарифмически нормальном распределении могут возникать ситуации, когда среднее по выборке растет, а рыночная стоимость падает.

Авторы выражают признательность редакционной коллегии журнала «Большой Каталог Недвижимости» (г. Санкт-Петербург) и президенту ассоциации риелторов Санкт-Петербурга и Ленинградской области Ф.В. Дьячкову, предоставившим электронную базу журнала, которая была использована для опубликованных в настоящей статье примеров.