Особенности изготовления препрегов для длинномерных изделий из композиционных материалов с термопластичным связующим
Автор: Скульский Олег Иванович
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 3 т.12, 2019 года.
Бесплатный доступ
Технология получения деталей из композиционных материалов с термопластичным связующим отличается от традиционной, испопьзующей в этом качестве термореактивные смолы, и требует новых конструкторскх и технологическх решений. В данной статье предложен двухстадийный способ изготовления длинномерной углеродной несущей жилы высоковольтных проводов: на первой стадии на углеродную нить наносится термопластичный слой из расплава полиэфирэфиркетона, на второй - из нитей формируется жила и обжимается методом гидродинамического волочения. С помощью метода конечных элементов построена численная модель процесса нанесения слоя термопласта на углеродную нить в осесимметричной фильере. Для описания реологических свойств расплава полиэфирэфиркетона выбрана обобщенная модель Карро и определены входящие в нее материальные константы. Рассчитаны поля скоростей, давления и температуры, дана оценка влияния приложенного давления и скорости протяжки жилы на толщину наносимого слоя. Для стадии формирования и пропитки жилы, состоящей из покрытых термопластичным слоем углеродных нитей, в предположении, что каждая из нитей в жиле в процессе обжатия находится в одинаковых условиях, на основе аналитического решения задачи плоскорадиальной фильтрации получено безразмерное уравнение для положения фронта пропитки пористой углеродной нити под действием внешнего линейно распределенного по каналу волоки давления...
Композиционные материалы, углеродная нить, термопластичное связующие, реологические свойства, полиэфирэфиркетон, численная модель, толщина слоя, фронт пропитки
Короткий адрес: https://sciup.org/143168907
IDR: 143168907 | УДК: 532.5.032+66.011 | DOI: 10.7242/1999-6691/2019.12.3.29
Текст научной статьи Особенности изготовления препрегов для длинномерных изделий из композиционных материалов с термопластичным связующим
Полимерные композиционные материалы (ПКМ) с матрицами из термопластичных полимеров типа полиэфирэфиркетона, полифенилсульфида, поликарбоната и подобных появились на рынке менее 10 лет назад [1–4]. По сравнению с композиционными материалами на основе термореактивных смол [5–7] композитные термопластичные материалы обладают рядом преимуществ: высокой прочностью, повышенной стойкостью к ударным нагрузкам, химической стойкостью, пониженной токсичностью, ремонтопригодностью. К недостаткам следует отнести высокую температуру переработки, высокую вязкость расплава и низкую адгезионную способность. Композиты на основе полиэфирэфиркетона (Polyether Ether Ketone — PEEK), по сравнению с реактопластичными материалами, не требуют проведения реакции полимеризации в процессе формования изделия и обеспечивают возможность переработки и вторичного использования.
Традиционная технология получения деталей из термореактивных композиционных материалов (КМ), армированных непрерывными волокнами, заключается в следующем: сначала готовится полуфабрикат, далее препрег, который затем раскраивают, выкладывают в пакет и формуют лист или деталь [8, 9]. При создании длинномерных изделий, например, несущих жил высоковольтных проводов, препрег состоит из нитей, содержащих несколько сотен углеродных волокон. Однако специфические свойства термопластичных связующих — высокая вязкость растворов и расплавов, высокая температура перехода в вязкотекучее состояние, зависимость свойств от степени кристалличности и скорости охлаждения, низкая адгезионная способность термопластов, вносят коррективы в каждую из операций при изготовлении из них изделий.
Принимая во внимание эти особенности, предлагается вести процесс в две стадии: сначала углеродные нити покрывать слоем PEEK, затем формировать из них жгут и протягивать его через фильеру в режиме гидродинамического волочения. Такой способ обеспечит более равномерное начальное макрораспределение связующего в жиле и более глубокую пропитку нитей. Разработка математической модели процесса пропитки термопластичным связующим углеродных нитей на основе аналитических и численных методов механики сплошных сред и теории фильтрации позволит обосновано выбрать схему и параметры процесса получения длинномерных изделий из углеродных композиционных материалов с термопластичным связующим.
2. Реологическая модель термопластичного связующего
Реологические измерения связующего PEEK_G151_eng были проведены на кафедре «Конструирование и технологии в электротехнике» Пермского национального исследовательского политехнического университета на реометре DHR-2 TA Instruments [11]. Полученные в диапазоне скорости деформации
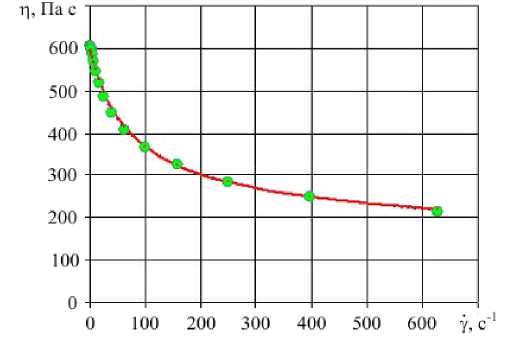
Рис. 1. Зависимость динамической вязкости от скорости деформирования: экспериментальные данные (точки) и аппроксимирующая кривая (сплошная линия).
1 > у < 700 с-1 при температуре T = 360 + 370 ° C данные (см. Рис. 1) хорошо аппроксимируются обобщенным уравнением Карро (Carreau):
П — П „
П 0 -П „
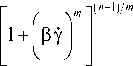
exp ( - b ( T - 360) ) , (1)
где n — эффективная вязкость. В расчетах использовались следующие значения параметров модели: n 0 = 600 Па с; П „ = 120 Па с; Р = 0,02 с; m = 6; n = 0,4; b = 0,4 . Теплофизические свойства приведены в таблице 1.
Таблица 1. Теплофизические свойства материалов
|
Название материала |
Плотность р , кг/м3 |
Теплоемкость C p , дж/(кг ° С) |
Теплопроводность X , Вт/(м ° С)) |
Температура плавления T , ° С пл |
|
Углеродное волокно |
1700 |
1000 |
0,8 |
– |
|
PEEK_G151_eng |
1320 |
1340 |
0,25 |
343 |
-
3. Нанесение термопластичного слоя на нить (I-я стадия)
-
3.1. Особенности устройства для нанесения термопластичного слоя на углеродные нити
-
-
3.2. Математическая модель процесса нанесения термопластичного слоя
Устройство для нанесения термопластичного слоя на нить, состоящую из сотен углеродных волокон, может быть встроено в существующую линию получения нитей из реактопластов путем замены ванны с валками (Рис. 2) на термостатируемый блок с пакетом фильер, одна из которых представлена на рисунке 3. Геометрия фильеры обуславливается конструкторскими решениями. Управление процессом осуществляется через технологические параметры: скорость протяжки нити V 0 , давление на входе в канал P 0 и температуры T 0 , Ts и Tg .
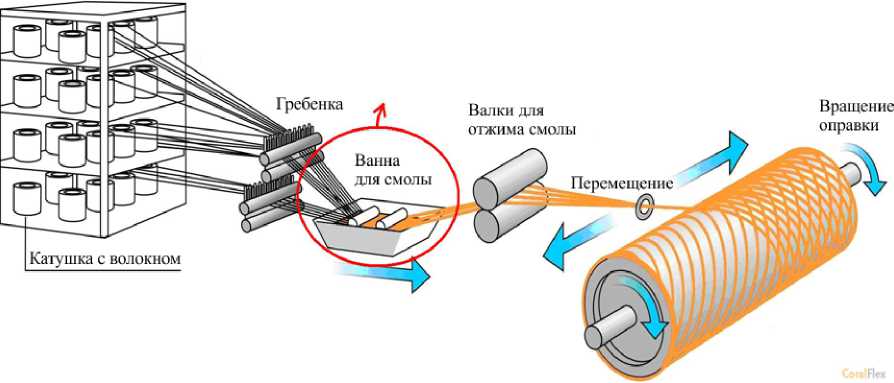
Рис. 2. Схема оборудования для пропитки углеродных нитей из реактопластичных смол
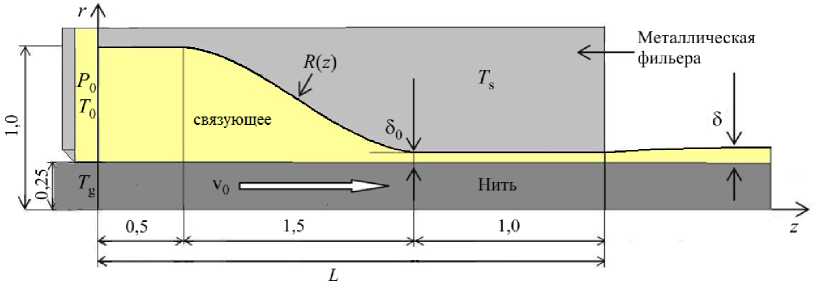
Рис. 3. Схема фильеры (размеры даны в миллиметрах)
на углеродную нить
Стационарное неизотермическое течение несжимаемого термопластичного связующего описывается системой дифференциальных уравнений в частных производных, отражающих законы сохранения импульса, массы и энергии [12–14]:
pv -Vv =-Vp + V-^pV( vT + v )j,(2)
V-v = 0,(3)
pCp (v •V)T = V- (XV T),(4)
где v — вектор скорости, p — давление, p — плотность, Cp — удельная теплоемкость, X — коэффициент теплопроводности, п — эффективная вязкость, определяемая согласно уравнению (1).
Задача расчета течения в формующей оснастке ставилась в цилиндрической системе координат с учетом осевой симметрии. Предполагалось, что: на входе в канал поступает жидкость под давлением P 0 с температурой T 0 ; температура стенок канала Ts поддерживается постоянной; углеродная нить поступает в фильеру с температурой Tg ; на твердых границах выполняются условия прилипания. Диссипация механической энергии считалась пренебрежимо малой.
Согласно процедуре Галеркина краевая задача (1)–(4) преобразуется в полуслабую вариационную формулировку с естественными граничными условиями по напряжениям [15–21]. В цилиндрической системе координат с учетом осевой симметрии система уравнений имеет вид:
LLR (f 1 Ч ( д v д v A (0 u u A u v 0 ur (0 vr A 0 ur (0 vr d vz Al
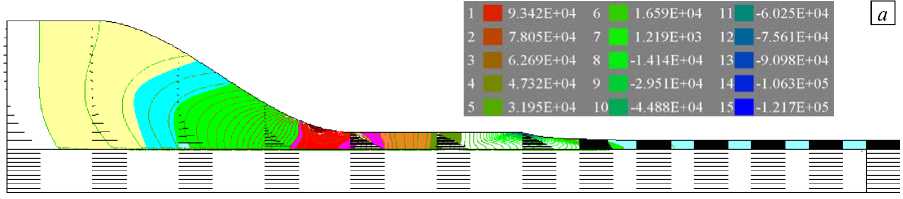
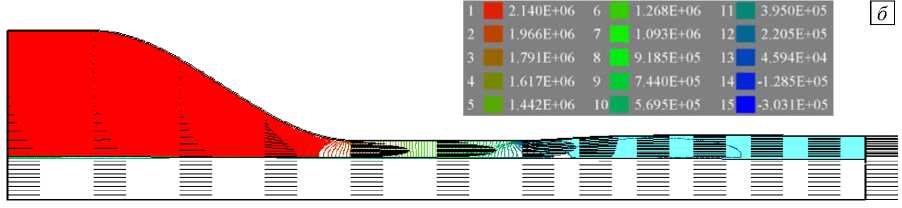
2n 0 0 [ r I r dr z 0z J ( 0r r J r2 0r ( 0r J 0z ( 0z 0r J J LR(.z) Г ( dv 0v A du du (dv A 0u (5v 0v A] 2n u, I vr—- + vz—- 1+---p + 2n —-1 —- l + n —z-1 —r- +—z- If rdrdz = 2n u7S7rdr, I ” [ ( dr dz J dz dz ( dz J dr ( dz dr JJ* L R(z) 2п* * ф v, 0v, 0v, A , , „ — +--+--| rdrdz = 0, r dr dz J . LLRI) Г dT dT, (дФ<р0T дфдTAl , ,„ 2п <фр C„ (v, — + v, —) + X--+---\drdrdz = 0, 00 0 1 p dr z dz (dr dr dz dz JJ где Sz — компонента вектора поверхностной нагрузки, по величине равная давлению во входном сечении канала, ur,uz — компоненты векторной взвешивающей функции, ф — скалярная взвешивающая функция; L — длина фильеры. На свободной поверхности наносимого слоя, форма которой определяется из условия vr дR (z)+ v 0R (z) д t zдz ’ задаются условия отсутствия нормальных напряжений. Форма свободной поверхности наносимого слоя вычисляется на каждом шаге итерационного процесса по разностным формулам Ri = Ri-1+ vr- Uzz') vz( ) до выполнения условия равенства нулю нормальной составляющей скорости. Задача (5)–(10) решалась методом конечных элементов по официально зарегистрированной программе «FEM FLOW» [22]. При этом численная реализация полученной нелинейной системы сводится к решению последовательности линеаризованных задач, в которых нелинейные члены определяются по результатам предыдущих итераций. Сначала рассматривается линеаризованная задача течения с постоянной вязкостью, затем, с учетом известных с предыдущего шага компонент вектора скорости, — задача конвективного теплопереноса. Далее, по найденному температурному полю корректируется эффективная вязкость, а по полю скоростей вычисляются конвективные члены в температурной задаче и уточняется положение свободной границы. Процесс повторяется до достижения заданной точности. На каждой итерации дискретизация линеаризованных задач осуществляется треугольными конечными элементами с линейной аппроксимацией компонент вектора скорости и температуры, а давление принимается кусочно-постоянным в пределах четырехугольников, состоящих из двух треугольных элементов. Контроль сходимости итерационного процесса выполняется по эффективной вязкости. Граничные условия первого рода для скорости и температуры удовлетворяются непосредственно присваиванием заданных значений соответствующих переменных в граничных узлах. 3.3. Расчет режимов процесса нанесения полимерного слоя на углеродную нить Основное отличие термопластов от термореактивных смол при использовании в качестве связующего состоит в необходимости создания для них высокотемпературного поля в зоне течения. Кроме того, важно обеспечить прогрев поступающей углеродной нити выше 346°С — температуры плавления термопласта в бескислородной среде, для исключения интенсивного окисления углерода. На рисунке 4 представлены результаты расчета температурного поля в фильере при температуре поступающего расплава 370°С и температуре нити на входе 360°С. На рисунке 5 приведены поля скоростей и давлений в формующей оснастке без приложенного на входе давления (Рис. 5а) и при давлении 2 МПа. Скорость протяжки нити 0,1 м/с. Результирующая толщина наносимого слоя зависит от следующих управляющих параметров: геометрии инструмента; реологических свойств расплава термопласта; температурных режимов; скорости протяжки нити; давления на входе в фильеру. Три первых параметра считаются заданными, а влияние приложенного давления и скорости протяжки на толщину наносимого слоя представлено в таблице 2. Приведенные данные позволяют выбрать технологические параметры для получения требуемой толщины слоя термопласта углеродной нити. Рис. 4. Распределение температуры в фильере: температура поступающего расплава Тs = 370oC, температура жилы на входе Т0 =360oC Рис. 5. Распределение давления и профили скорости в фильере без давления на входе (а) и при P0 = 2 МПа (б) Таблица 2. Радиус получаемой нити (х103, мм) и относительная толщина наносимого слоя термопласта 5/80 (величина в круглых скобках) Давление на входе P0, МПа 0,1 0,5 1,0 2,0 Скорость протяжки V0, м/с 0,5 304 (0,54) 304 (0,54) 304 (0,54) 305 (0,55) 0,1 304 (0,54) 306 (0,56) 308 (0,58) 312 (0,62) 0,05 304 (0,54) 308 (0,58) 312 (0,62) 320 (0,70) 0,02 306 (0,56) 314 (0,64) 324 (0,74) 342 (0,92) 0,01 308 (0,58) 324 (0,74) 342 (0,92) 377 (1,27) 0,005 312 (0,62) 342 (0,92) 377 (1,27) 448 (1,98) 0,002 324 (0,74) 395 (1,45) 483 (2,33) 606 (3,56) После охлаждения нить, окруженная слоем термопласта, может непосредственно использоваться в производстве препрегов в виде ткани с последующим формованием объемных изделий на стандартном прессовом оборудовании.
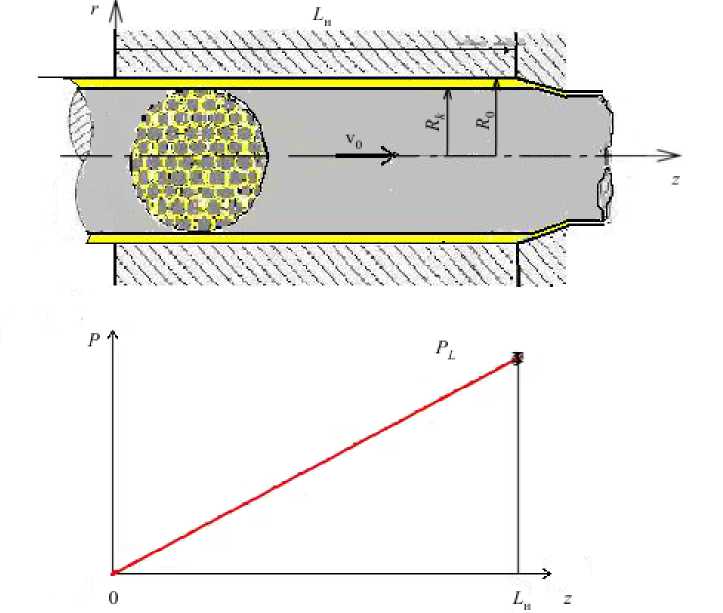
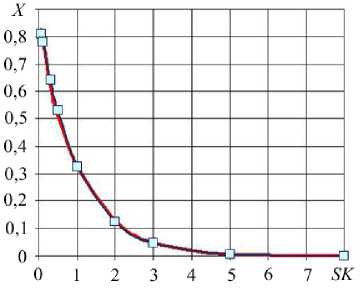
4. Обжатие и пропитка углеродной жилы (II-я стадия) При изготовлении длинномерных изделий (труб, стержней, несущих жил высоковольтных проводов и другого) требуется дополнительная операция для формирования жилы: составляющие ее нити, окруженные слоем термопластичного связующего, следует обжать в режиме гидродинамического волочения при температуре выше температуры плавления термопласта (Рис. 6). В результате расплавленный слой термопласта под действием сжимающих напряжений заполняет пространство между нитями и проникает в поры между волокнами. Далее считается, что все нити в жиле находятся в одинаковых условиях. Рис. 6. Схема процесса обжатия жилы в режиме гидродинамического волочения и характер распределения давления в каждой нити по длине напорной насадки волоки Степень пропитки отдельной нити, состоящей из пучка углеродных волокон, окруженных слоем термопласта, находящейся под действием постоянного сжимающего давления на внешнем контуре, можно рассчитать, воспользовавшись формулой Дюпеи [22], вытекающей из закона Дарси [23–26], записанного для плоскорадиальной фильтрации: (^2 - R2f)In(Rk(Rf ) = 2KPkt ц m где Pk — давление на контуре нити, K — коэффициент фильтрации, ц — вязкость, m — пористость, t — время пропитки, Rk, Rf — радиусы контура и фронта пропитки. В рассматриваемом случае распределение давления линейно по длине напорной насадки Lн волоки. Такая связь давления с продольной координатой z при постоянной скорости протяжки жилы v0 однозначно определяет зависимость давления от времени движения материальной частицы по каналу волоки t = z/v0 : P — = Pl — t, LLLL нн t e 0,^0 , _ Lн _ где максимальное давление в слое связующего на выходе из напорной насадки равно PL = 6^о L н (Rо - Rk )2. Используя закон Дарси, запишем выражение для скорости фильтрации wr : wr K дP (r, t) ц m дr Подставив (13) в условие несжимаемости - + - = 0, придем к уравнению для давления: r д r 1 dP (r, t) d2P (r, t) ---1--i----= 0 , r dr dr2 решение которого с учетом граничных условий (при r = Rk ^ P = PL и при r = R, ^ P = 0) имеет вид: P ( r, t ) = Pl Lн ( '1 V — ln (Rk/r)' ln (Rk!R, )J. Запишем (13), приняв во внимание выражение для давления (15) и скорость фильтрации как производную радиуса по времени — wr = dr]dt, получим дифференциальное уравнение rdr = v0 KPL L„ цm In (Rk/R,) t dt , решение которого дает формулу для расчета радиуса фронта пропитки Rf при линейном распределении давления по длине канала, отличающуюся от формулы Дюпеи (11): (Rk — Rf) In (Rk/R, ) = v0KPLt2 L „ Ц m Рис. 7. Сравнение решения уравнения (18) (сплошная кривая), и аппроксимирующего выражения (19) (линия с маркерами) Формулу (17) удобно представить в безразмерном виде. Rf Для этого введем переменную X = —— и безразмерный Rk комплекс, включающий все параметры процесса, SK = V0 KPLt2 /(ц mRk2). В результате получим трансцендентное уравнение (X2— 1) In (X) = SK , (18) справедливое для любого набора задаваемых параметров, дающее оценку степени пропитки углеродной нити термопластичным связующим. Уравнение (18) решим один раз, воспользовавшись аппроксимирующим выражением: X = 0,886exp (—0,981 SK), обеспечивающим приемлемую точность в диапазоне значений 0,1 < SK< 10 (Рис. 7). Приведем пример оценки пропитки нити в процессе гидродинамического волочения с параметрами: Lв= 0,01м, R0= 4,5-10—4м, Rk = 3,5■10—4м, v0= 0,01 м/с, K = 10—12м2 ц = 400 Па■ с, m = 0,5. При этом: - распределение давления по длине следующее: P = PL —, где максимальное давление в волоке составляет Lн PL = 2,4 -107Па; - время воздействия давления на движущуюся нить определяется по формуле t = — и равно 1 с; v0 - значение безразмерного параметра SK = 0,979 ; – X приближенно равно 0,339; - радиус фронта пропитки Rf = RkX = 1,186 ■ 10—4м. В данном случае относительная площадь пропитки Rk2 — нити достигает Rk2 R2 100% = 88,5%.
5. Заключение Основной проблемой производства длинномерных углетермопластиков является трудность пропитки углеродных волокон высоковязким связующим. Предложенный двухстадийный способ — сначала нанесение термопластичного слоя на углеродную нить, а затем формирование и обжатие жилы методом гидродинамического волочения — позволяет улучшить качество пропитки и с минимальной модернизацией использовать существующее технологическое оборудование. Разработанная математическая модель дает возможность рассчитать поля давления и температуры, кинематику течения и оценить влияние технологических параметров на толщину наносимого на нить термопластичного слоя. Требуемая толщина слоя определяется из условия равенства площадей поперечных сечений наносимых слоев и суммарной площади пустот между нитями и между углеродными волокнами. Полученное на основе аналитического решения задачи плоскорадиальной фильтрации безразмерное уравнение для положения фронта пропитки пористой нити под действием внешнего линейно распределенного по каналу волоки давления дает возможность оценить степень пропитки углеродных нитей термопластичным связующим и позволяет прогнозировать степень однородности готового изделия.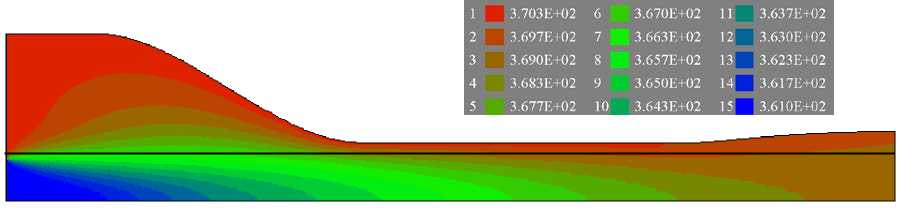
Список литературы Особенности изготовления препрегов для длинномерных изделий из композиционных материалов с термопластичным связующим
- O'Bradaigh C.M. Sheet forming of composite materials // Flow and rheology in polymer composites manufacturing / Ed. S.G. Advani. Elsevier, 1995.
- Johnson A.F. Rheological model for the forming of fabric-reinforced thermoplastic sheets // Composites Manufacturing. 1995. Vol. 6. P. 153-160.
- Johnson A.F., Picket A.K. Numerical simulation of the forming process in long fibre reinforced thermoplastics // WIT Transactions on Engineering Sciences. 1996. Vol. 10. P. 233-242.
- Сироткин О.С., Андрюнина М.А., Бейдер Э.Я. Новые конструкционные и функциональные ПКМ на основе термопластов и технологии их формования // Авиационная промышленность. 2012. № 4. С. 43-47.
- Chen X., Zhang Y., Shilin Y. Two-dimensional simulations of resin flow in dual-scale fibrous porous medium under constant pressure // J. Reinforc. Plast. Compos. 2013. Vol. 32. P. 1757-1766.
- Yang B., Tang Q., Wang S., Jin T., Bi F. Three-dimensional numerical simulation of the filling stage in resin infusion process // J. Compos. Mater. 2016. Vol. 50. P. 4171-4186.
- Бейдер Э.Я., Петрова Г.Н. Термопластичные связующие для полимерных композиционных материалов // Труды ВИАМ. 2015. № 11. С. 40-49.
- Saad A., Echchelh A., Hattabi M., El Ganaoui M., Lahlou F. Numerical simulation and analysis of flow in resin transfer moulding process // FDMP. 2012. Vol. 8. P. 277-294.
- Doi M., Edwards S.F. The theory of polymer dynamics. Oxford University Press, 1986. 404 p.
- Сильченков Д.Г., Гришин С.В., Гладков И.Б. Композиционный несущий сердечник для внешних токоведущих жил проводов воздушных высоковольтных линий электропередачи и способ его производства. Патент РФ № 2386183 от 10.04.2010 г.
- Ершов С.В. Пространственное течение расплавов полимеров в канале зоны дозирования пластицирующего экструдера и формующего инструмента / Дисс... канд. тех. наук: 01.02.05. Пермь, ПНИПУ, 2018. 119 с.
- Кузнецова Ю.Л., Скульский О.И. Исследование реологических моделей растворов полимеров на реометрических течениях // Математическое моделирование в естественных науках. 2013. С. 92-94.
- Скульский О.И., Аристов С.Н. Механика аномально вязких жидкостей. М.-Ижевск: Регулярная и хаотическая динамика, 2004. 154 с.
- Кузнецова Ю.Л., Скульский О.И. Влияние режимов течения на расслоение сдвигового потока жидкости c немонотонной кривой течения // ПМТФ. 2019. Т. 60, № 1. С. 27-36.
- Сегерлинд Л. Применение метода конечных элементов. М., Мир, 1979. 392 с.
- Zienkiewicz O.C, Taylor R.L., Zhu J.Z. The finite element method. Its basis and fundamentals. Butterworth-Heinemann, 2013. 756 p.
- Cook R.D., Malkus D.S., Plesha M.E. Concepts and applications of finite element analysis. Wiley, 1989. 637 p.
- Pickett A.K., Queckbörner T., de Luca P., Haug E. An explicit finite element solution for the forming prediction of continuous fibre-reinforced thermoplastic sheets // Composites Manufacturing. 1995. Vol. 6. P. 237-243.
- Jenny P., Lee S.H., Tchelepi H.A. Adaptive fully implicit multi-scale finite-volume method for multi-phase flow and transport in heterogeneous porous media // J. Comput. Phys. 2006. Vol. 217. P. 627-641.
- Димитриенко Ю.И., Левина А.И., Боженик П. Конечно-элементное моделирование локальных процессов переноса в пористых средах // Вестник МГТУ им. Н.Э. Баумана. Серия: Естественные науки. 2008. № 3. C. 90-103.
- Димитриенко Ю.И., Шугуан Ли. Конечно-элементное моделирование неизотермического стационарного течения неньютоновской жидкости в сложных областях // Математическое моделирование и численные методы. 2018. № 2. C. 70-95.
- Скульский О.И., Фонарев А.В., Кузнецова Ю.Л. «FEM FLOW» - конечно-элементная программа для расчета течения вязкоупругой жидкости в каналах со свободной поверхностью с учетом неизотермичности: cвидетельство об официальной регистрации программы для ЭВМ № 2007611760 от 25.04.2007.
- Баренблатт Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах. М.: Недра, 1984. 211 с.
- Маскет М. Течение однородных жидкостей в пористой среде. М.: Институт компьютерных исследований, 2004. 641 с.
- LeBel F., Fanaei A.E., Ruiz É., Trochu F. Prediction of optimal flow front velocity to minimize void formation in dual scale fibrous reinforcements // Int. J. Mater. Form. 2014. Vol. 7. P. 93-116.
- Димитриенко Ю.И., Богданов И.О. Многомасштабное моделирование процессов фильтрации жидкого связующего в композитных конструкциях, изготавливаемых методом RTM // Математическое моделирование и численные методы. 2017. № 2. C. 3-27.


