Особенности эквивалентных преобразований сопротивлений схем треугольника и звезды в П- и Т-образных фильтровых структурах

катушек, а в другом – емкостей параллельных конденсаторов, где к = 1, 2, ..., n , а n — общее число реактивных элементов схем. Буквой g ₀ на рис. 1 и 2 обозначены нормированные сопротивления генератора, если g ₁ соответствует емкостному элементу и проводимости генератора, если величине g ₁ соответствует индуктивный элемент. Кроме того, на рис. 1 и 2 буквой g n _{+ 1} обозначены нормированные сопротивления нагрузки, если g_n соответствует емкостному элементу и проводимости нагрузки, если величине g_n соответствует индуктивный элемент. Фильтры, в которых величины n четные, представлены на рис. 1 и 2, а . Фильтры с нечетными n оканчиваются элементами на рис. 1 и 2, б и являются симметричными устройствами. Используя полученные для фильтров – прототипов низких частот параметры g_k , с помощью частотного преобразования определяются значения нормированных параметров элементов сначала электрической, а затем и конструктивной схем фильтра [4]. В результате на основе эквивалентных преобразований фильтров – прототипов, описываемых параметрами g_k , реализуются разные типы фильтров.

При проектировании резонансных систем автогенераторов и генераторов, управляемых напряжением, широко используются П- и Т-образные фильтровые структуры, способы построения которых принципиально отличается от традиционных приемов разработки филь © Баранов А.В., Козиков А.Л., 2019

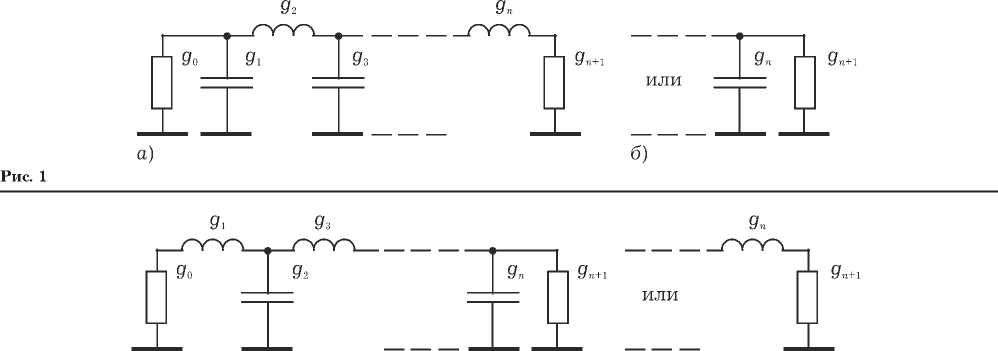
Рис. 2

а)                                                           б)

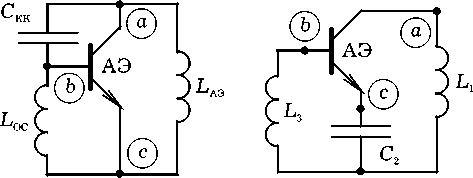
Рис. 3

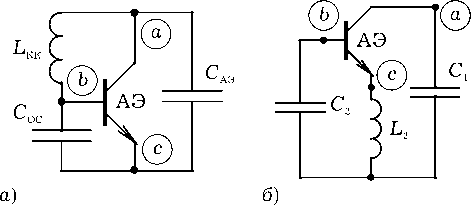
Рис. 4

тров [6; 7]. В данных случаях обычно применяются эквивалентные преобразования треугольника сопротивлений в звезду и, наоборот, сопротивлений звезды в треугольник [7; 8].

Несмотря на то что П- и Т-образные фильтровые структуры достаточно хорошо исследованы [1–5], особенно при решении задач фильтрации, вопросы эквивалентных преобразований импедансов в треугольных и звездообразных схемах этих структур не рассматривались. Цель статьи – изучить особенности указанных эквивалентных преобразований как в процессе выполнения задач фильтрации, так и при проектировании резонансных систем автогенераторов.

В первом случае применим эквивалентные преобразования сопротивлений в треугольных и звездообразных схемах при проектировании резонансных систем трехточечных автогенераторов. Поскольку необходимым условием работы любого генераторного устройства является вполне определенные способы подключения к электродам транзистора трех реактивных элементов, рассмотрим на рис. 3 и 4 типовые [9] (а) и синтезированные в работе [8] (б) обобщенные эквивалентные трехточечные схемы автогенераторов. Элементы всех схем предполагаются чисто реактивными, то есть применяются лишь емкости С1, С2, С3, СОС, CКК, САЭ и индуктивности L1, L2, L3 , LОС, LКК, LАЭ (или эквивалентные емкости или индуктивности соответствующих идеальных контуров, подключенных к электродам транзистора). Так же, как и в работе [8], для обозначения словосочетаний «активный элемент», «обратная связь» и «колебательный контур» использованы индексы «АЭ», «ОС» и «КК». А для замены слов: «коллектор», «база» и «эмиттер транзисторов» на рисунках под буквой б применены цифры «1», «2» и «3». В представленных трехточечных схемах генераторов соответствующие точки обозначены буквами а, б и с. Неотмеченные точки в звездообразных трехточечных схемах генераторов являются центральными точками звезды. Схемы устройств на рис. 3 и 4 представляют собой треугольные (а) и звездообразные (б) трехточечные схемы генераторов, которые в зарубежной литературе [10] называют, соответственно, автогенераторами с параллельной и последовательной обратной связью.

Из условий эквивалентности электрических цепей на рис. 3 и 4, а и б , когда на участках, ограниченных точками а , б и с , токи и напряжения остаются неизменными, следует, что величины комплексных импедансов элементов схем связаны известными соотношениями [11]

для преобразования треугольника сопротивле-

•  ее

•              •               •

^ний Z а_Э , Z _кк, Z ос в звезду Z _b Z 2 , Z з :

Z =

I

Z з =

•                 •

■ ^Z 2 =

Z КК Z аэ
1 Z аэ	•                             е + Z ОС+ Z KK •                  е Z аэ z ос
1 Z аэ	•                             е + Z OC + Z КК •                 • Z КК Z ОС

,

,

I

^Z АЭ + ^Z ОС + ^Z КК

I

и наоборот – сопротивлений звезды в треуголь-

ник:
z аэ	• = Z1	I + Z 2	+
■ Z ОС	1 = Z 2	l + Z 3	+
Z KK	• = Z1	I + Z 3	+

^Z 1 ^Z 2

Z 3 ’

^Z 2 ^Z 3

Z1

• e

^Z1^z з

Z 2

,

.

Считая импедансы в выражениях (1) и (2) чисто реактивными, в работе [8] получены взаимные условия, при которых трехточечные схемы генераторов под буквами а и б на рис. 3 и 4 являются эквивалентными:

I X 1 X 3, > | Х 1 X 2 + X 2 X 3,

IXкк| > XАЭ + Xос|

где X1, X2, X3, XОС, XКК, XАЭ – сопротивления соответствующих реактивных элементов схем. Данные сопротивления определяются с помощью общих для каждого из генераторов на рис. 3, 4 выражений: Zос = jXос, Zаэ = jXаэ, ZКК = jXКК, Z1 = jX 1, Z2 = jX2, Zз = jX3. Причем для любых емкостных и индуктивных элементов: Xс < 0, Xl > 0, так как

Zc = , X c = , а

C j ton C    C     ton C пп

Z L = j ®п L, X L = ®п L, где Юп — циклическая частота преобразования, для которой выполняются взаимные соотношения (1) и (2). В генераторной технике эта частота совпадает с частотой генерации.

Полученные неравенства (3) и (4) являются следствием того, что величины сопротивлений реактивных элементов трехточечных генераторов не могут быть произвольными, они удовлетворяют системам установленных ограничений [8]:

^X аэ ^x ос > 0, ^X аэ ^x кк < 0, I ^X ОС | < | ^X аэ| I ^X ОС I < | ^X кк|

I X 1 X 3 >  0, 1 X 2 X 3 <  0,

П ^X 3I <  X 11 11 ^X 2| <  X 11

Неравенства (5) и (7) означают, что реактивности элементов Zаэ и Zос (Z1 и Z3) должны иметь одинаковые, а реактивности элементов Zкк и Zос (Z2 и Z3) — разные знаки. Иными словами, если XАЭ и XОС являются индуктивными сопротивлениями, то XКК – это емкостное сопротивление, а трехточка называется индуктивной (см. рис. 3, а). Возможен второй вариант построения схемы автогенератора, когда XАЭ, XОС могут быть сопротивлениями емкостей, а XКК должно быть только индуктивным сопротивлением. В этом случае трехточка называется емкостной (см. рис. 3, б).

При выполнении неравенств (6) и (8) в автогенераторе реализуется условие минимальной обратной связи. Оно необходимо для обеспечения режима работы его активного элемента без захода в перенапряженный режим, который характеризуется повышенными уровнями фазо- вых шумов и высших гармонических составляющих. На практике минимальная обратная связь реализуется в тех случаях, когда, например, в схемах на рис. 3, а и 4, а индуктивность Lос выбирается меньшей по величине по сравнению с Lаэ, а величина Сос — большей по сравнению с Саэ [6].

Если при соблюдении ограничительных мер (5)–(8) выполнить условия (3) и (4), то трехточечные схемы автогенераторов на рис. 5 и 6, а и б также можно считать эквивалентными. Они получены путем преобразования схем устройств на рис. 3 и 4 к новому виду, когда их активные элементы (транзисторы с общим эмиттером) охвачены внешними обратными связями параллельного ( а ) и последовательного ( б ) типов. Особенностью генераторов под буквами а и б на рис. 5 и 6 является использование в их эквивалентных схемах разных типов фильтровых структур: в одних случаях – фильтров нижних частот (ФНЧ), в других – фильтров верхних частот (ФВЧ). Автогенератор обычно работает на частотах генерации, которые соответствуют падающему участку АЧХ фильтровой структуры, а не там, где потери цепи обратной связи минимальны. В этом смысле неважно, какого типа будет фильтр в цепи внешней обратной связи генератора. Падающий участок АЧХ одинаково

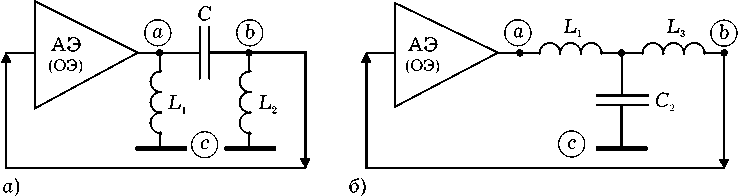
Рис. 5

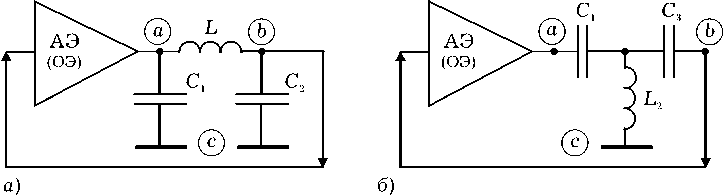
Рис. 6

присутствует как в ФНЧ, так и в ФВЧ. Более того, в общем балансе фаз автогенератора противоположные знаки фаз коэффициентов передач фильтровых структур ФНЧ и ФВЧ принципиально не меняют кратность 2п по отношению к целому числу.

Таким образом, несмотря на использование разных типов фильтровых структур (ФНЧ и ФВЧ), схемы генераторов под буквами а и б на рис. 5 и 6 остаются эквивалентными с точки зрения теории цепей, так как получены для одинаковой в сравниваемых устройствах частоты генерации, где справедливы эквивалентные преобразования сопротивлений их элементов.

Во втором случае применим эквивалентные преобразования импедансов в треугольных и звездообразных схемах при выполнении задач фильтрации, используя для этого П- и Т-образные фильтровые структуры на рис. 1 и 2.

Если в фильтре-прототипе низких частот на рис. 1 (к + 2) < (n + 1) и элемент gk представляет собой нормированную емкость, то выражения для нормированных сопротивлений к-, (к + 1)- и (к + 2)-го элементов имеют вид:

v^н — j v^h — ^Юп

Z k = — ----,    Z k + 1 = j---g k + 1 ,

юп               Юс gk юс

н

Zk+2 = Юп

—gk + 2

Ю с

где Ю с — циклическая частота среза, которая соответствует определенным в работе [3] величинам характеристик затухания.

Используя выражения (9) в соотношениях (1) и (2), а также учитывая, что параметры gk являются одинаковыми для схем на рис. 1 и 2, получим формулу для расчета частоты преобразования юп:

^ю п

= ю с

д k ⁺ g k g k + 2 ^- g k + 1 g k + 2 g k g k + 1 g k + 2

Можно показать, что вид формулы (10) будет таким же и в случае, когда в фильтре-прототипе низких частот на рис. 2 при условии (k + 2) < (n + 1) элемент gk представляет собой нормированную индуктивность, а выражения для нормированных сопротивлений k-го, (k + 1)-го и (k + 2)-го элементов схемы записываются в виде н _ • юп „   ^Н _   -j      ^н     • юп „

Z k = j ^g k , Z k + 1 = —------, Z k + 2 = j ^g k + 2 .

Юс            юп _              Юс с           — gk+1            с юс

Формула (10) имеет смысл, если выполняется следующее неравенство:

g k ⁺ g k g k + 2 >  g k + g + 2 .                         ⁽¹¹⁾

Для табличных значений параметров g k , g k ₊ 1 и g k ₊ 2 неравенство (11) выполняется всегда. По сути, неравенство (11) имеет тот же физический смысл, что и соотношения (3) и (4). В частном случае – для симметричных фильтровых структур, когда g k = g k ₊ 2 , соотношения (11) и (3), (4) совпадают с точностью до знака неравенства. Противоположные знаки в неравенствах (11) и (3), (4) являются главной особенностью эквивалентных преобразований треугольника сопротивлений в звезду (и наоборот) в процессе выполнения рассмотренных задач – фильтрации и проектирования резонансных систем автогенераторов. Эта особенность фактически обусловлена наличием разных «граничных условий»

или ограничений при достижении выбранных технических целей. В генераторной технике такими ограничениями являются условия (5)–(8), а в технике фильтров – требование получения в фильтрах-прототипах одинаковых амплитудночастотных характеристик с заданной величиной их затухания.

Второй важной особенностью эквивалентных преобразований треугольных и звездообразных сопротивлений при выполнении рассмотренных задач являются разные частоты, для которых справедливы эти преобразования. В первом случае им соответствуют частоты генерации, во втором – частоты преобразования вычисляются по формуле (10).

Таким образом, в данной работе отмечены две особенности эквивалентных преобразований сопротивлений схем треугольника и звезды в П- и Т-образных фильтровых структурах, которые используются как в процессе выполнения задач фильтрации, так и при разработке резонансных систем автогенераторов. Для достижения указанных технических целей первая особенность связана с необходимостью соблюдения неравенств (11) и (3), (4). Вторая особенность обязывает проводить эквивалентные преобразования звездообразных и треугольных сопротивлений в автогенераторах на частотах генерации, а в фильтровых структурах – на частотах, вычисляемых по формуле (10). Обе эти особенности необходимо учитывать в эквивалентных преобразованиях треугольных и звездообразных сопротивлений рассматриваемых схем.