Особенности моделирования процесса полунепрерывного прессования алюминиевых сплавов

Полунепрерывное прессование длинномерных пресс-изделий является одним из основных способов изготовления строительных профилей из алюминиевых сплавов, причем одним из главных сдерживающих факторов повышения производительности процесса является низкая скоростьпрессования. В свою очередь, выбор скоростного режима прессования ограничен прежде всего тепловыми условиями, которые влияют на эффективность процесса прессования. Выбор оптимальных температурно-скоростных условий является одной из главных задач технолога при разработке процесса прессования, поскольку от этого зависит эффективностьпроцесса и уровень физико-механических свойств пресс-изделия [1]. Одним из эффективных методов управления тепловыми условиями процесса прессования алюминиевых сплавов является принудительное испарительное охлаждение прессового инструмента, в частности применение принудительно охлаждаемой форкамерной матрицы (ПОФМ). Однако внедрение в производство данной технологии сдерживается недостатком теоретических знаний и экспериментальных данных в этой области. Поэтому моделирование формоизменения и тепловых условий прессования алюминиевых сплавов с ПОФМ является актуальной задачей.

Наряду с классическими теоретическими методами математического моделирования процессов ОМД (методом совместного решения уравнений равновесия с условием пластичности; методом баланса работ; методом верхней оценки; методом линий скольжения и др.) в последние десятилетия широкое применение получили численные методы. Практически численными методами можно решитьлюбую задачу, так как увеличение ее размерности и усложнение геометрии приводит лишьк увеличению объема вычислений. В то же время при моделировании процессов прессования на основе метода конечных элементов (МКЭ) реализованного с помощью коммерческих пакетов программ Deform-3D, PressForm, AutoForge, QForm и других в силу специфических особенностей процесса прессования исследователи сталкиваются с определенными трудностями [2].

Отмечено, что модель МКЭ должна применяться с помощью физически обоснованной методики и базироваться на экспериментальных линиях равных скоростей (изотахах) и зонах деформирования металла в контейне- ре, полученных методами визиопластичности и координатных сеток [3; 4].

В работе [4] показано, что данные скоростей течения, полученные с применением МКЭ, качественно близки, но мало пригодны для количественной оценки при приближении к промышленным значениям коэффициента вытяжки (более 40). Это неуклонно ведет к росту ошибки в расчетах скоростей и энергозатрат до 20 %. Коммерческие пакеты МКЭ можно рассматриватьдля применения на промежуточном этапе в виде теста между эскизным проектом и его воплощением в рабочую документацию для промышленности, нонев качестве средства для точного расчета технологических параметров из-за больших расхождений результатов с экспериментальными данными (10…20 %) против погрешностей по классическим расчетам, обычно составляющих не более 5 % [3].

Повыситьсходимостьрезультатов виртуального эксперимента, полученных численным моделированием (МКЭ), и реального эксперимента позволяет корректировка реологии деформируемого металла. В работах [5; 6] описаны методики уточнения зависимости сопротивления деформации от параметров процесса (степени, скорости и температуры деформации). Сутьметодов заключается в корректировке коэффициентов уравнения реологии деформируемого металла путем сравнении усилия деформации полученного в результате расчета по аналитической зависимости [5] или виртуального эксперимента [6], c истинным усилием процесса прессования. Применение данных методик позволяет минимизировать ошибкувопределенииэнергосиловыхитемпературно-ско-ростных параметров процесса с 10…20 до 1…5 %. С другой стороны, использование только компьютерного моделирования при оптимизации технологических параметров процесса прессования сложных профилей привело бы к постановке большого количества виртуальных экспериментов, что в разы увеличит сроки проектирования технологии. Поэтому требуется разработатьтакую методику проектирования технологического процесса, которая позволила бы говоритьо сходимости результатов не только реального и виртуального эксперимента, но и компьютерной и аналитической модели. Это позволит еще на начальной стадии проектирования технологии оптими-зироватьтемпературно-скоростные и силовые парамет- ры полунепрерывного прессования с учетом адекватной аналитической модели.

На основании вышеизложенного предлагается следующая методика создания виртуальной модели процесса полунепрерывного прессования длинномерных строительных профилей из алюминиевых сплавов.

• 1.    Вводим геометрию профиля и температуру на выходе из матрицы.

• 2.    Вводим характеристики горизонтального гидравлического пресса (модель, усилие, скоростной диапазон прессования и т. д.).

• 3.    Вводим реологию алюминиевого сплава по зависимости, предложенной в работе [7]:

• 4.    Определяем температурно-скоростные и силовые условия полунепрерывного прессования на основе математической модели, полученной в результате решения сопряженной краевой задачи нестационарной теплопроводности, представленной в работе [1]. При этом геометрия профиля пересчитывается на эффективный диаметр. Находим опорное решение по температурно-скоростному режиму прессования, заключающееся в определении максимально возможной скорости прессования (МВСП) с учетом ограничений по предельной температуре, скорости и допускаемому усилию.

• 5.    Проводим виртуальный эксперимент полунепрерывного прессования по тому же эффективному диаметру прессуемого профиля, что ив п. 4, в пакете инженерного анализа Deform-3D.

• 6.    Сопоставляем результаты по температурно-скоростным и силовым параметрам прессования математического моделирования с виртуальным экспериментом. В случае отклонения результатов проводим корректирующие воздействия на сравниваемые модели. Сначала – на параметры компьютерной модели – путем уменьшения размеров конечных элементов с целью повышения точности расчета. Если сходимостьне достигнута, тогда уточняем математическую модель, в которой корректируется влияние объемных источников тепла на конечную температуру профиля. Корректировку продолжаем до достижения заданной точности, в результате чего находим опорное решение, адекватно описывающее процесс полунепрерывного прессования, которое можно приме-нитьдля дальнейшей оптимизации конструктивных элементов матрицы с целью достижения заданного качества пресс-изделия.

σ _s = A ⋅ ε ^B ⋅ ξ ^C ⋅ exp(– D ⋅ T _пр)МПа, (1) где А , B , C , D – реологические коэффициенты; ε = ln(l) – степеньдеформации; ξ = ε / t – скоростьдеформации, 1/с; T _пр – температура прессования, ^оС.

Рассмотрим компьютерное моделирование процесса прессования строительного профиля КП 45302-1 (рис. 1) из сплава АД31 на горизонтальном гидравлическом прутково-профильном прессе усилием 25 МН с применени-емПОФМ.

Размеры заготовки принимали 215 × 780 мм. Прессование проводили из контейнера диаметром 225 мм. Для поиска опорного решения перестроили матрицу на эффективный диаметр ( d _эф=29,4мм). Определение МВСП показало, что максимальная скорость прессования составляет 10 мм/с. Дальнейшее повышение скорости прессования возможно только за счет введения в технологический процесс принудительного охлаждения. Для этого была разработана ПОФМ с выступом, на котором расположено кольцо, а внутри выступа находится рабочая по-лостьфоркамеры, при этом наружная поверхностьвыс-

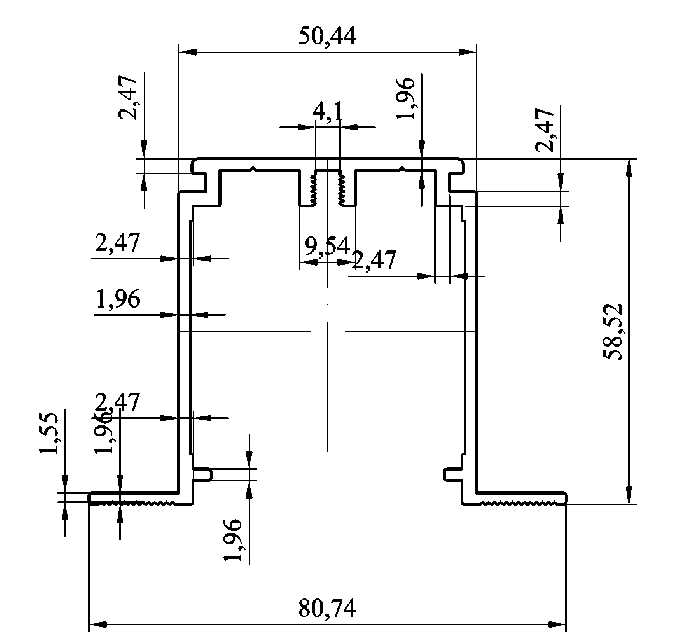
Рис. 1. Эскиз профиля

тупа эквидистанта внешнему контуру рабочей полости форкамеры и снабжена охлаждающими каналами особой конструкции. Расчет показал, что применение принудительного испарительного охлаждения позволит уве-личитьскоростьпрессования до 12 мм/с.

Для сопоставления математической и компьютерной модели по предложенным скоростным условиям прессования выполнен виртуальный эксперимент (ВЭ), исходные параметры которого представлены в таблице.

Исходные данные виртуального эксперимента

Параметр прессования ВЭ	Значение (ВЭ с ПОФМ по эффективному диаметру)
Начальная температура, оС
– нагрева заготовки	480
– контейнера	440
– форкамерной матрицы	410
Скоростьпрессования, мм/с	12
Коэффициент трения
– в контейнере	0,5
– в форкамере	0,5
– в матрице	0,2
Высота пресс-остатка, мм	25

Геометрия виртуальной модели процесса полунепрерывного прессования и разбивка объектов модели на конечные элементы показаны на рис. 2и3 соответственно.

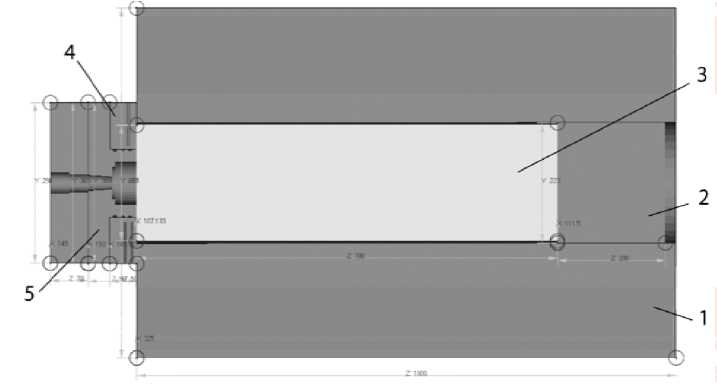
Рис. 2. Схема виртуальной модели полунеперерывного прессования сПОФМв пакете инженерного анализа Deform-3D: 1 – контейнер; 2 – пресс-штемпель; 3 – слиток;

4 – кольцо; 5 – матрица

Расчет проводили на двухпроцессорной ПЭВМ с тактовой частотой 2ГГц, объем ОЗУ–4Гб. Время решения задачи составило 121 ч.

В результате моделирования в Deform-3D построена координатная сетка (рис. 4), которая имеет характерные для прессования застойные зоны в контейнере и форкамере, резкое увеличение скорости истечения металла в осевой зоне на выходе из матрицы и запаздывание периферийных участков заготовки, что качественно не противоречит известным экспериментальным исследованиям.

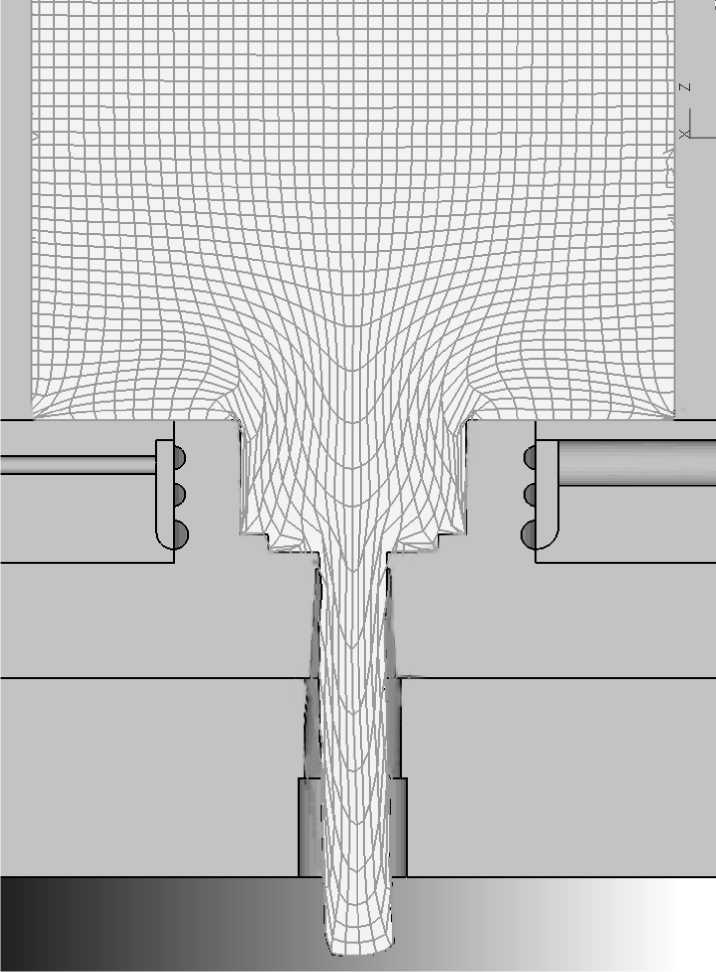
Рис. 4. Характер течения металла по результатам моделирования в Deform-3D

Сравнение энергосиловых параметров процесса полунепрерывного прессования компьютерной модели (рис. 5) и теоретического расчета показало достаточную сходимостьданных. Усилие прессования по аналитической модели составило 12,3 МН, а максимальное усилие компьютерной модели, согласно рис. 4, – 12,1 МН. При

абв

г

Рис. 3. Конечные элементы объектов виртуальной модели: а – слиток; б – наружное кольцо; в – форкамерная матрица по эффективному диаметру; г – форкамерная матрица по рабочему чертежу профиля

рассмотрении стадий процесса полунеперывного прессования по изменению усилия прессования наблюдается четыре характерных зоны. В первой зоне (с 1-й по 12-ю секунду) происходит распрессовка металла в контейнере, далее выдавливание металла в форкамеру (с 12-й по 14-ю секунду) и прессование через очко матрицы с образованием характерного «горбика» на диаграмме (на 14-й секунде).

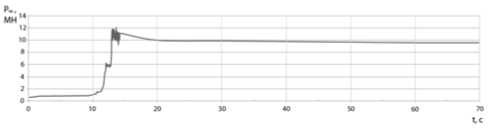
Рис. 5. Зависимостьусилия прессования от времени по результатам компьютерного моделирования

Сравнение значений температуры поверхности отпрессованного профиля на выходе из ПОФМ компьютерной модели с результатами виртуального эксперимента (рис. 6) показало достаточную сходимостьдля инженерных расчетов (ошибка не превышает 5 %).

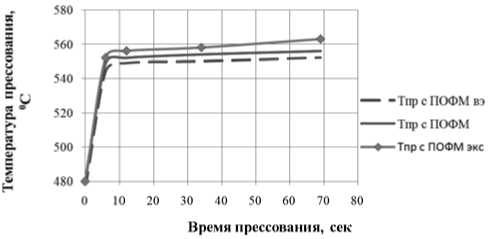
Рис. 6. Изменение выходной температуры строительного профиля КП 45302-1 из сплава АД31 при полунепрерывном прессовании на горизонтальном гидравлическом прессе усилием 25 МН: Тпр с ПОФМ и Тпр с ПОФМвэ – расчетные значения выходной температуры профиля с использованием ПОФМ по аналитической и компьютерной модели соответственно; Тпр сПОФМэкс–экспериментальные значения

Хорошая сходимость результатов моделирования и экспериментальных данных позволяет использовать вир- туальную модель для дальнейшей доработки конструкции матрицы с целью обеспечения требуемого качества пресс-изделия.

Таким образом, в данной работе представлена методика проведения виртуального эксперимента процесса полунепрерывного прессования длинномерных строительных профилей из алюминиевых сплавов. Проведено компьютерное моделирование процесса прессования строительного профиля из сплава АД31. Сравнительный анализ полученных результатов показал возможность применения данной методики на практике при отимиза-ции технологии прессования и проектировании прессового инструмента, что в конечном счете должно привести к сокращению расходов при проектировании новой и усовершенствовании действующей технологии полунепрерывного прессования алюминиевых сплавов.