Особенности обнаружения лоцирующих сигналов радиотехническими устройствами охранной сигнализации
Автор: Воловач В.И.
Журнал: Вестник Ассоциации вузов туризма и сервиса @vestnik-rguts
Рубрика: Информационные процессы и системы
Статья в выпуске: 1 т.2, 2008 года.
Бесплатный доступ
Рассмотрены особенности обнаружения сигналов с различными параметрами на входе приемников радиотехнических устройств охранной сигнализации на фоне внутриприемного гауссовского шума. Определены параметры радиосигнала, характеризующие объект и характер его движения.
Короткий адрес: https://sciup.org/140208942
IDR: 140208942
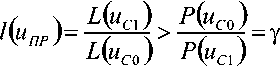
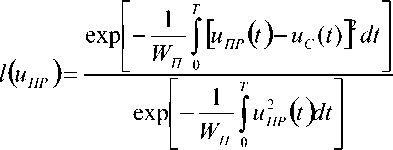
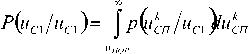
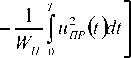
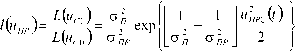
Список литературы Особенности обнаружения лоцирующих сигналов радиотехническими устройствами охранной сигнализации
- Воловач В.И. Обнаружение объектов в условиях априорной неопределенности относительно параметров движения//Проблемы и решения современной технологии. Сб. науч. трудов ПТИС. Выпуск 5. Часть II. -Тольятти: ПТИС, 1999. С. 62-66.
- Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. -М.: Радио и связь, 2004. -608 с.
- Хьюбер Дж. П. Робастность в статистике: Пер. с англ. -М.: Мир, 1984. -304 с.
- Тихонов В.И. Оптимальный прием сигналов. -М.: Радио и связь, 1983. -336 с.
- Артюшенко В.М., Воловач В.И. Точность измерения параметров движения в условиях изменяющейся дальности//Сборник научных трудов ГАСБУ. Техника и технология сервиса. -М.: ГАСБУ, 1997. С. 47-54.
Статья научная
