Особенности преподавания математики в естественно-техническом лицее

С момента основания Саранского городского естественно-технического лицея математика являлась одним из профилирующих предметов. Однако она никогда не велась как предмет с углубленным изучением. В качестве основной программы выбрана программа для общеобразователь ных классов в 8-9-х классах и программа курса В в старших классах.

В 1998/99 учебном году было проведено анкетирование учащихся лицея с целью выявления их отношения к различным предметам. Ребятам было предложено несколько вопросов.

• 1.    Домашние задания по каким предметам вы делаете с интересом (с удовольствием)?

• 2.    Назовите три предмета, которые вам нравятся. Полученные ответы распределись таким образом:

  
  
  
  
  
  
  
  
  

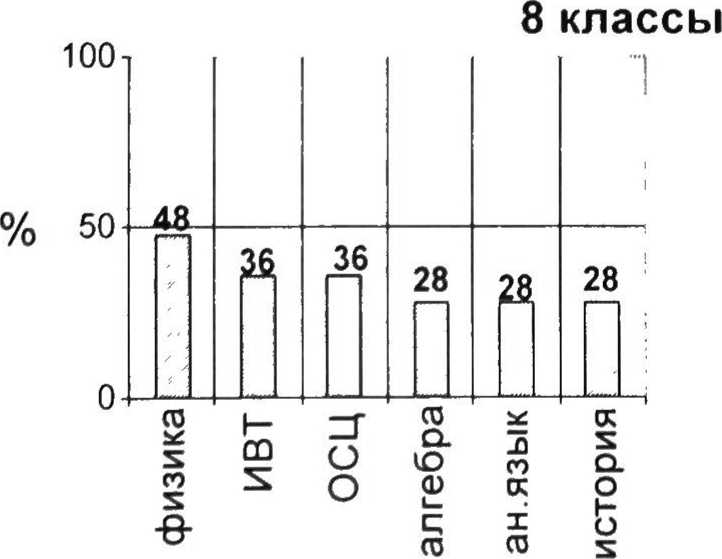
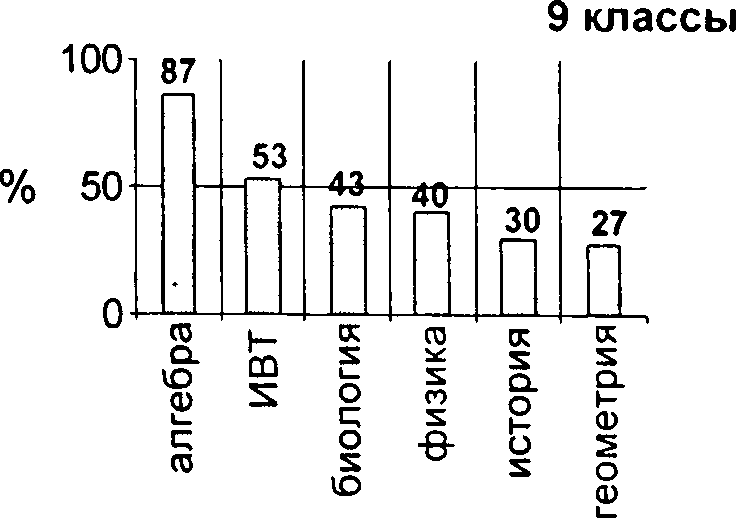
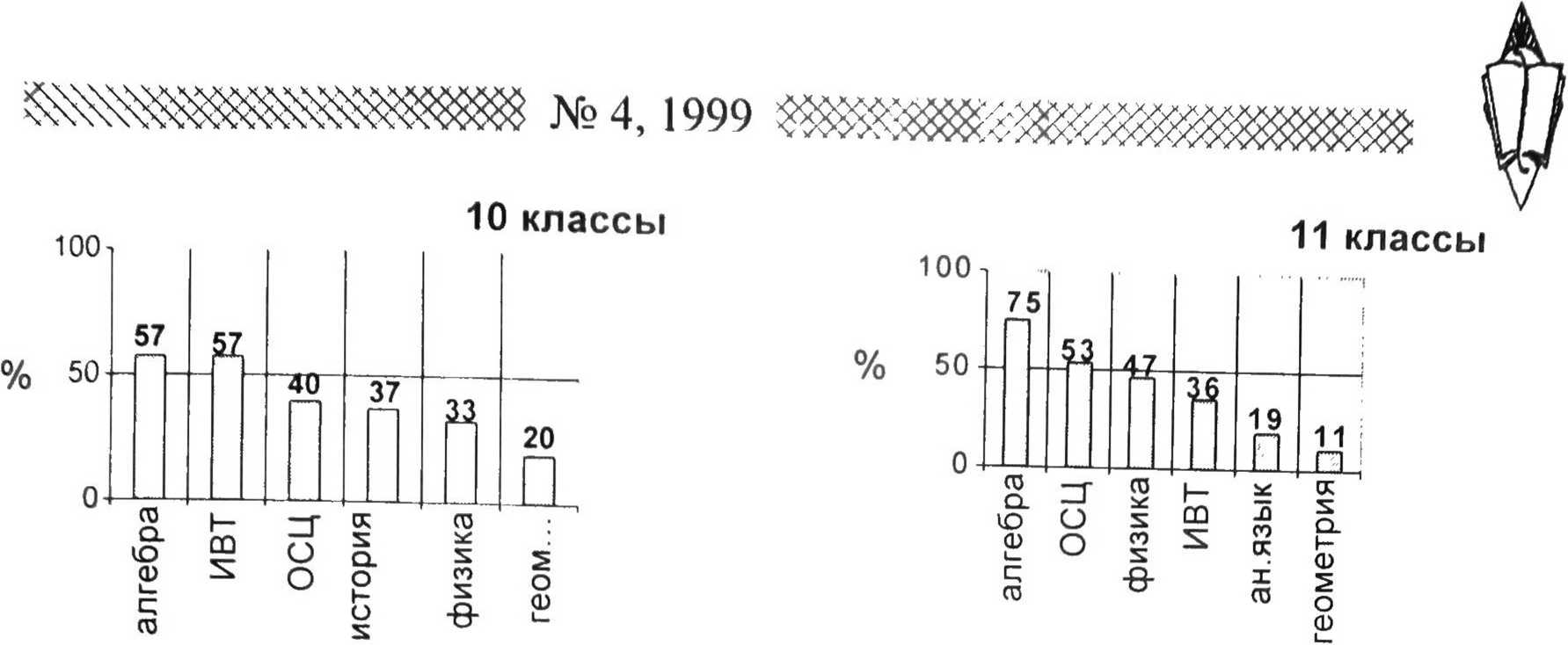
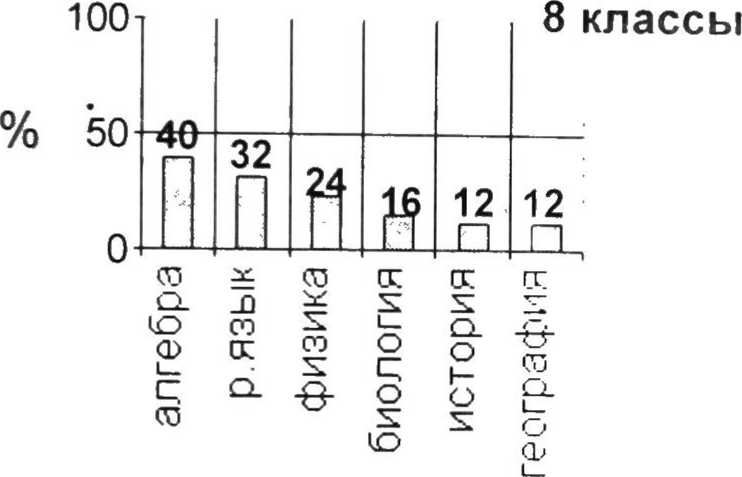
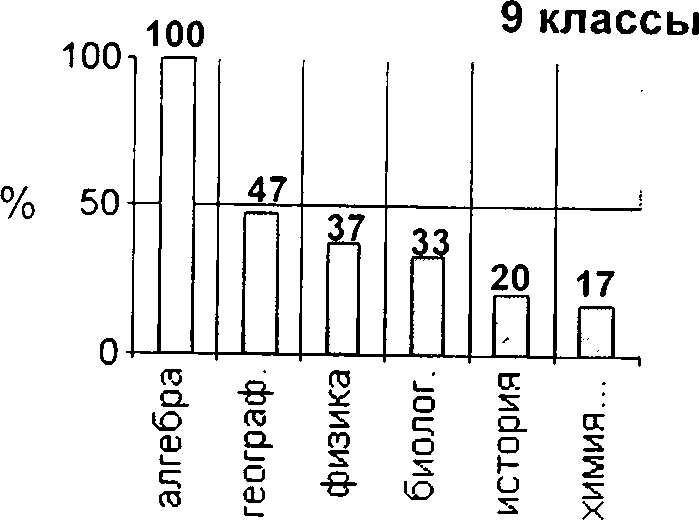
• 3.    На каких уроках вы получаете наиболее устойчивые знания? Полученные ответы:

  
  
  
  
  
  
  
  
  

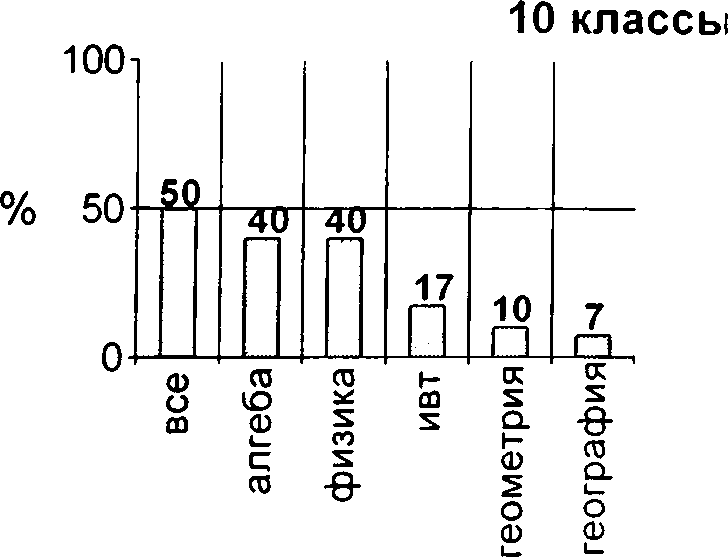
  11 классы

  
  
  
  
  

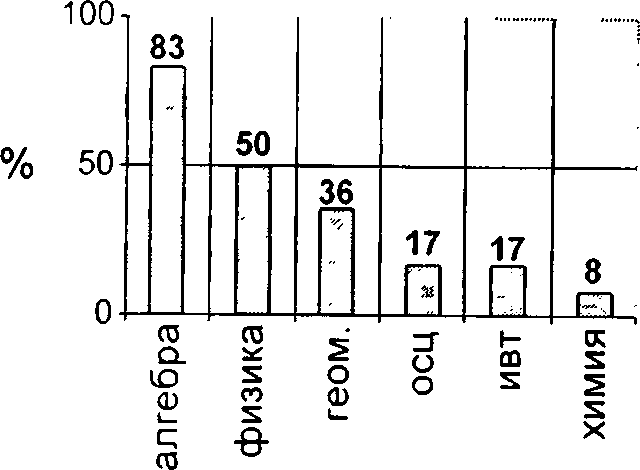
Ответы на этот вопрос распределились следующим образом:

8 классы

По приведенным диаграммам видно, что при поступлении в лицей, т.е. в 8-м классе, в большинстве случаев интересы ребят еще разбросанны. Нет явного предпочтения того или иного предмета. Но уже начиная с 9-го класса у лицеистов одним из самых «уважаемых» предметов становится алгебра. Об интересе к изучению математики говорит и тот факт, что при выборе выпускных экзаменов в 9-х и 11-х классах более 70 % лицеистов называют алгебру или геометрию. Таким образом, можно констатировать, что стратегия в преподавании математики учителями лицея выбрана правильно.

Анализ результатов тематических контрольных работ в 8-х классах (за 1995-1998 гг.) выявил, что наихудшие знания и умения показывают лицеисты при изучении первой темы - “Неравенства” Это обусловлено следующими причинами:

- одним из наиболее сложных умений, которое должно быть выработано при изучении данной темы, является умение доказывать неравенства на основании свойств числовых неравенств. Способы доказательства, по сравнению со всем изучавшимся ранее материалом, являются наименее формализованными.

Поэтому, как и при решении текстовых задач, особенно востребовано логическое мышление учащихся. Но материал учебника алгебры для 7-го класса, к сожалению, содержит очень малое количество задач и упражнений, способствующих его развитию;

• -    анализ ошибок, допускаемых учащимися в контрольной работе на тему “Неравенства”, позволяет говорить о высоком проценте вычислительных ошибок. а также ошибок, допускаемых при сложении алгебраических дробей;

• -    контрольная работа по теме “Неравенства” - первая, которую ребята пишут в лицее. Сказывается то, что учащиеся еще не совсем привыкли к смене обстановки, учителей, требований. На этом фоне у них возникают неуверенность в себе, некоторая растерянность, несобранность.

Базовая программа 8-го класса при изучении темы “Неравенства” предусматривает решение простейших систем линейных неравенств с одним неизвестным. Подавляющее большинство упражнений учебника на эту тему составляют задачи на решение систем, состоящих только из двух неравенств. И лишь в одном (!) упражнении присутствуют примеры систем, содержащих три неравенства. Также следует заметить, что из рассмотрения совершенно исключены двойные неравенства. Ни в одной школьной программе (за исключением программ для классов с углубленным изучением математики) не встречается упоминание о таком понятии, как «совокупность» неравенств или уравнений. Однако каждому математику ясно, насколько важно это понятие. И без его использования бывает просто невозможно решать многие виды уравнений и неравенств.

С учетом названных причин была составлена программа факультативного курса по математике для 8-го класса лицея. Первая тема этого курса - “Множества”, в рамках которой рассматриваются простейшие вопросы теории множеств: понятие множества; способы записи и обозначений множества; конечные, бесконечные и пустые множества, подмножества; виды числовых множеств; пересечение и объединение множеств. Изучение названных вопросов по- зволяет подготовить лицеистов к восприятию темы “Система и совокупность” более точно осмыслить понятие функции.

Следующая тема факультативного курса - “Совокупности неравенств” Недостаток часов не позволяет уделять ей много времени на уроках. Поэтому основной материал изучается на факультативе.

В базовой программе курса алгебры 8-го класса предусматривается знакомство учащихся с понятиями уравнений и неравенств, содержащих неизвестное под знаком модуля. Формирование умений решать такие уравнения и неравенства не предусматривается. Однако подобные задачи и примеры часто встречаются на вступительных экзаменах в вузы. Само понятие модуля, оказывается, достаточно сложно для понимания школьника. Но оно необходимо при изучении темы “Арифметический квадратный корень из степени” Поэтому рассмотрению темы “Модуль. Уравнения и неравенства, содержащие модуль” выделен большой блок факультативного курса.

Также в факультативный курс 8-го класса включены разделы:

• -    “Внесение множителя под знак арифметического квадратного корня и вынесение множителя из-под знака арифметического квадратного корня” Более сложные примеры на названную тему позволяют учащимся глубже осознать математический смысл понятия арифметического квадратного корня;

• -    “Решение неравенств высших степеней методом интервалов”

Базовый курс алгебры 8-го класса предусматривает изучение темы “Приближенные вычисления. Простейшие вычисления на микрокалькуляторе” Из программы лицея названные темы исключены. Приближенные вычисления и погрешности приближений подробно рассматриваются в лабораторном практикуме по физике. Кроме того, к 8-му классу подавляющее большинство детей уже умеют хорошо пользоваться различными видами микрокалькуляторов.

Из анализа контрольных работ за 1995 - 1998 гг. следует, что наибольшие затруднения учащиеся 9-х классов испытывают при изучении темы “Степенная

®Ш№»«№ №4, 1999 функция” В данной теме впервые начинает проводиться достаточно серьезный анализ функции, и это является сложным для восприятия детей. В рамках темы "степенная функция” также изучаются способы решения иррациональных уравнений.

Наиболее хорошо в 9-м классе усваиваются темы: “Степень с рациональным показателем", “Прогрессии” В 9-м классе вводятся понятия степени с целым, а затем, как обобщение, с рациональным показателем. Но свойства степеней и правила действий с ними такие же, как и для степеней с натуральным показателем. Поэтому изучение первой из этих тем является обобщающе-закрепляющим для раздела математики, изучение которого начинается в 7-м классе. Тема “Прогрессии” не вызывает затруднений, так как, во-первых, объем предлагаемого теоретического материала является очень малым. Во-вторых, хорошие показатели учащихся позволяют сделать вывод о наличии у них основ логического и структурного мышления, которое начинает вырабатываться в ходе изучения таких тем, как доказательство неравенств, решение текстовых задач и др.

Усреднение баллов, полученных на контрольных работах в 10-х классах за 1995 - 1998 гг., показывает, что хуже всего усваивается тема, в которой необходимо научиться производить тождественные преобразования различного вида тригонометрических выражений. Этот факт можно объяснить обилием тригонометрических формул, требуемых для запоминания и, в связи с этим, трудностью в выборе той из них, которая наиболее рациональна для применения в каждом конкретном случае.

На достаточно хорошем уровне усваиваются такие темы, как решение показательных и логарифмических уравнений и неравенств. При прохождении названных разделов повторяются и обобщаются уже известные методы решения уравнений и неравенств. Поэтому большин

ство приемов решений уже хорошо известны учащимся.

Если сравнить средние баллы, получаемые на контрольных работах по различным темам, изучаемым на протяжении 8-11-х классов, то можно увидеть, что наибольшие затруднения возникают при начальном изучении принципиально новых понятий, требующих в какой-то мере нестандартного мышления. Однако высокие средние баллы ребят на итоговых контрольных работах (и особенно в выпускных классах) показывают, что в результате все изучаемые математические понятия усваиваются лицеистами на оптимальном уровне.

С 1996- 1997 учебного года мной ведется разработка пакета йндивидуальных заданий для учащихся лицея по курсу алгебры 10-го класса. В настоящее время составлены четыре задания: «Повторение материала курса алгебры 7-9-го классов», «Решение показательных уравнений и неравенств», «Логарифм» и «Решение логарифмических уравнений и неравенств». Каждое задание (кроме третьего) содержит 20 вариантов. В первом задании варианты равносильны по степени сложности. Во втором и четвертом сложность заданий возрастает с увеличением номера варианта. Третье задание состоит из пяти номеров по 10 пунктов в каждом. Это задание заранее выдается ученикам, а затем на одном из уроков учитель дает каждому ученику по одной задаче из каждого номера и проверяет правильность решения на том же уроке.

Индивидуальные задания состоят из задач такого уровня сложности, который определяется необходимым уровнем подготовки учащихся к вступительным экзаменам во втузы. При этом самые легкие варианты содержат задачи минимально необходимого уровня, более сложные варианты включают задания, решение которых показывает высокое усвоение лицейской программы, а также задачи повышенной сложности.