Особенности применения преобразований Нортона при согласовании импедансов с различными коэффициентами трансформации

В процессе проектирования усилительно-преобразовательных устройств СВЧ-диапазона важной задачей является согласование сопротивлений их цепей, особенно с высоким коэффициентом трансформации в широком диапазоне рабочих частот, который можно достичь в пределах установленных Боде – Фано ограничений на полосы согласований произвольных импедансов [1; 2]. Широкополосное согласование цепей можно обеспечить, например, с помощью инвертирующих трансформаторов импедансов (K-, J-инвертеров) [3; 4], а также его можно выполнить, используя преобразования Нортона [5; 6] или метод крайних им-педансов [7]. Чаще широкополосное согласование осуществляется на основе теории фильтров [3; 8] в сочетании с трансформацией оконечного импеданса с помощью преобразования Нортона [9–12]. К сожалению, наличие различных, но правильных по сути форм записи преобразований Нортона [2; 5; 6; 8–13] может привести к ошибкам в процессе их применения в случаях повышающего или понижающего идеального трансформатора, то есть когда его коэффициенты трансформации больше или меньше единицы. В частности, коэффициенты пересчета элементов, стоящих за идеальным трансформатором, могут не соответствовать выбранной форме записи преобразований Нортона, как в публикации [9]. Цель данной статьи – при выполнении на основе теории фильтров широкополосного и узкополосного согласования импе-дансов в случаях с различными коэффициентами трансформации изучить особенности и следствия применения преобразований Нортона.

По аналогии с работой [8] рассмотрим на рис. 1 и 2 соответственно дуальные П- и Т-образные фильтровые структуры, в которых трансформация импедансов достигается путем включения идеальных трансформаторов в любую точку схем в соответствии с правилами 1 и 2.

Правило 1. Если используется повышающий трансформатор с соотношением напряжений в обмотках 1: m , то все расположенные после него последовательные импедансы умножаются на величину m ², а параллельные проводимости делятся на m ². На рис. 1 и 2 предполагается, что m > 1. Правило 2. Если используется понижающий трансформатор с соотношением 1:(1/ m ), то все расположенные после него параллельные проводимости умножаются на m ², а последовательные импедансы делятся на m ². Схемы, содержащие проводимость, параллельную Y , и последовательное сопротивление Z вместе с соответствующими идеальными трансформаторами 1: m и 1:(1/ m ) заменяются во всей полосе рабочих частот эквивалентными схемами на рис. 3 и 4 соответственно.

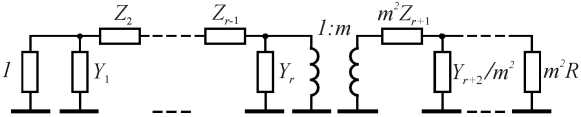
Рис. 1. Трансформация сопротивлений с использованием П-образной фильтровой структуры

Fig. 1. Transformation of resistances using a U-shaped filter structure

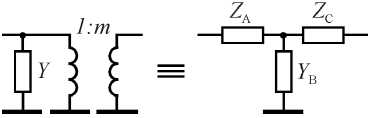
Рис. 3. Эквивалентные преобразования Нортона идеального повышающего трансформатора с проводимостью Y в Т-образную цепь

Fig. 3. Norton equivalent transformations of an ideal step-up transformer with conductance Y into a T-shaped circuit

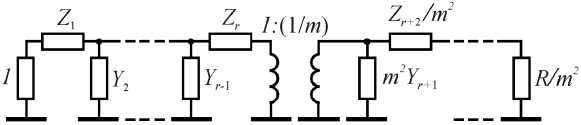
Рис. 2. Трансформация сопротивлений с использованием Т-образной фильтровой структуры

Fig. 2. Transformation of resistances using a T-shaped filter structure

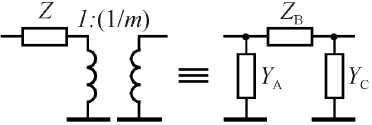
Рис. 4. Эквивалентные преобразования Нортона идеального понижающего трансформатора с импедансом Z в П-образную цепь

Fig. 4. Norton equivalent transformations of an ideal step-down transformer with impedance Z into a U-shaped circuit

кации [9] эти преобразования для схемы на рис. 4 полностью совпадают с обобщенными формулами (1) и (2). Вместе с тем существуют и другие формы записи преобразований Нортона. Например, если в выражениях (2) сделать замены m = 1/ n _Т и Z = 1/ Y , то получим представленные в работах [2; 5; 6; 10; 13] формулы для импедансов схемы на рис. 4 в зависимости от нового коэффициента трансформации n _Т:

2 nn

Z к = —T— Z ;   Z = —T— Z ; Z = n Z .

^A n T - 1 ^C 1 - n _T     ^{B T}

Если же в уравнениях (1) сделать те же замены, то для сопротивлений элементов схемы на рис. 3 справедливы соотношения, как в работах [2; 9; 10]:

n - 1 1 - n_T z

Z_k = -^ Z ; Z C = —T Z ; Z b = - . (4) ⁿ т n _T ⁿ T

С учетом произведенных замен m на n _Т трансформация импедансов достигается здесь путем включения идеальных трансформаторов в любую точку схем в соответствии с новым правилом 3.

Правило 3. Если n _Т = 1/ m при 0 <  n _Т< 1, то для повышающего и понижающего трансформаторов правила 1 и 2 меняются местами. То есть при использовании понижающего трансформатора с соотношением напряжений в обмотках 1: n _Т, (0 <  n _Т< < 1) все расположенные после него последовательные импедансы умножаются на ( n _Т)², а параллельные проводимости делятся на ( n _Т)². Если применяется повышающий трансформатор типа 1:(1/ n _Т) (0 <  n _Т< 1), то расположенные после него последовательные импедансы делятся на величину ( n _Т)², а параллельные проводимости умножаются

а                   б           в           г

Рис. 5. Эквивалентная замена идеального понижающего трансформатора с импедансом Z и проводимостью Y 1 ( а ) на зеркальную Г-образную цепь ( б ) и ее разновидности ( в , г )

Fig. 5. Equivalent replacement of an ideal step-down transformer with impedance Z and conductivity Y 1 ( a ) for a mirror L-shaped circuit ( b ) and its varieties ( c , d )

б             в          г

Рис. 6. Эквивалентная замена идеального повышающего трансформатора с проводимостью Y и импедансом Z 1 ( а ) на Г-образную цепь ( б ) и ее разновидности ( в , г )

Fig. 6. Equivalent replacement of an ideal step-up transformer with conductivity Y and impedance Z 1 ( a ) with an L-shaped circuit ( b ) and its varieties ( c , d )

а

б

Рис. 7. Эквивалентные замены идеального повышающего трансформатора с импедансом Z и с проводимостью Y* на аналогичную схему с проводимостью Y* /( n _т) 2 ( а ) и на обобщенную Г-образную цепь ( б)

Fig. 7. Equivalent replacements of an ideal step-up transformer with impedance Z and conductivity Y * for a similar circuit with conductivity Y* /( n _T)² ( a ) and for a generalized L-shaped circuit ( b )

на ( n _Т)². Таким образом, в зависимости от выбора m и ему соответствующих форм записи равнозначных по сути формул (1), (2) или (3), (4) преобразования Нортона предполагают применение разных правил 1, 2 и 3.

Преобразования Нортона могут быть также использованы для уменьшения числа элементов в полосовых фильтрах. Рассмотрим примеры уменьшения элементов, которые являются следствиями преобразований Нортона.

Для начала перед сопротивлением Z в схеме понижающего трансформатора на рис. 4 введем параллельно входу проводимость Y 1 . Выберем ее величину равной значению Y а в выражении (2) из условия Y 1 + Y а = 0. В этом случае полученная схема будет эквивалентна зеркальной Г-образной цепи на рис. 5, а , два элемента которой находятся по формулам:

Z        m ( m — 1)

Z- =    , Y_r =-------- , m = 1 + ZY .              (5)

^B m ^C Z ’            ¹

Вместе с тем, если на вход повышающего трансформатора с проводимостью Y (см. рис. 3) подключим последовательный импеданс Z1, величину которого выберем так, чтобы скомпенсировать сопротивление ZA в выражении (1), тогда новая схема становится эквивалентной Г-образной цепи на рис. 6, а, два элемента которой рассчитываются по формулам:

Y       m ( m - 1)

Y =    , Z =        , m = 1 + YZ .

^B m ^C Y              ¹

Полученные из уравнений (1) и (2) выражения (5) и (6) не теряют свои обобщенные и дуальные свойства. Они справедливы как в случае m > 1, так и при условии 0 < m < 1. В зависимости от первоначального выбора m запись уравнений (5) и (6) может быть также различной. Так, при m = 1/nТ и nТ > 1 элементы эквивалентных схем на рис. 7 и 8 с использованием понижающего 1:(1/nт) и повышающего 1:nт трансформаторов связаны следующи- ми соответствующими им соотношениями, как в литературе [2; 10]:

n — 1

Z_A = ——; Y = n Y ;

A   n T Y    B T n -1

Y_a = ^---; Z = n Z ;

^A    n _T Z    ^{B T}

*__ n т = 1 + Z Y,

___*

n _т = 1 + ZY ,

где Z * - последовательное по отношению к понижающему трансформатору 1:(1/ n _Т) сопротивление; Y * - параллельная повышающему трансформатору 1: n _Т проводимость. При получении формул (7) и (8) использовано правило 4.

а

б

Рис. 8. Эквивалентные замены идеального понижающего трансформатора с проводимостью Y и с импедансом Z* на аналогичную схему с импедансом Z* /( n _т)² ( а ) и на обобщенную зеркальную Г-образную цепь ( б)

Fig. 8. Equivalent replacements of an ideal step-down transformer with conductivity Y and impedance Z * for a similar circuit with impedance Z* /( n т )² ( a ) and for a generalized mirror L-shaped circuit ( b )

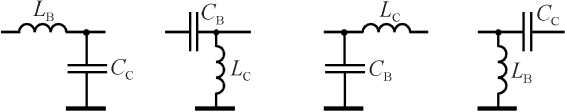
а              б                в              г

Рис. 9. Варианты реализаций обобщенных прямых и зеркальных Г-образных цепей на рис. 7 и 8 с частотно зависимыми коэффициентами трансформации

Fig. 9. Implementation options for generalized direct and mirror L-shaped circuits in Fig. 7 and 8 with frequency dependent transformation ratios

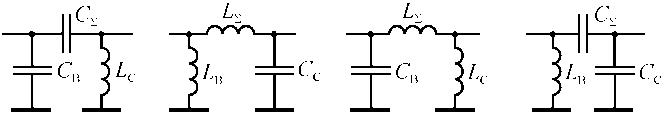
а               б                 в                г

Рис. 10. Комбинированные цепи, использующие рассмотренные на рис. 9 варианты, а также схемы ( в , г ) на рис. 5 и 6 для устройств с коэффициентами трансформации, которые не зависят от частоты

Fig. 10. Combined circuits using those discussed in Fig. 9 options, as well as schemes ( c , d ) in Fig. 5 and 6 for devices with transformation ratios that are independent of frequency

Правило 4. Два последовательных или параллельных элемента могут меняться местами. Величины установленных за идеальным трансформатором элементов с учетом коэффициентов трансформации согласно правилу 3 - Z */( n т) ² и Y */ / ( n _Т)² (см. рис. 8 и 7) – полностью компенсируют значения физически не реализуемых элементов Z с и Y с в формулах (1) и (2) соответственно или обнуляют в формулах (3) и (4) отрицательные сопротивления Z _C.

Таким образом, для уменьшения числа элементов в полосовых фильтрах могут быть использованы рассмотренные выше примеры эквивалентных преобразований Нортона. Одни преобразования предполагают использование параллельной проводимости Y 1 в схеме на рис. 5, а и последовательного сопротивления Z * в схеме на рис. 7, а , другие применяют последовательное сопротивление Z ₁ в схеме на рис. 6, а и параллельную проводимость Y * в схеме на рис. 8, а . Ниже отметим следствия данных преобразований.

Следствие 1. Параллельная проводимость Y1 в схеме на рис. 5, а и последовательное сопротивление Z* в схеме на рис. 7, а позволяют реализовать понижающие трансформаторы с помощью экви- валентных схем на рис. 5, б и 7, б, где величины элементов находятся по формулам (5) и (7). Вместе с тем последовательное сопротивление Z1 в схеме на рис. 6, а и параллельная проводимость Y* в схеме на рис. 8, а обеспечивают работу повышающих трансформаторов с использованием эквивалентных схем на рис. 6, б и 8, б, в которых величины элементов рассчитываются по формулам (6) и (8). Если предположить, что коэффициенты трансформации m и nТ в выражениях (5)–(8) не зависят от частоты го, то в ветвях, где располагаются Y1 и Z* (или Z1 и Y*), должны находиться одинаковые реактивные элементы (или только емкости, или только индуктивности, как на рис. 5 и 6 под буквами в и г).

Следствие 2. В свою очередь, если предположить, что коэффициенты трансформации m и nТ в выражениях (5)–(8) могут зависеть от частоты ω, то расположенные в ветвях схем элементы Y1 и Z* (или Z1 и Y*) должны иметь принципиально разные знаки реактивностей. Каждому индуктивному элементу должен соответствовать емкостнόй элемент и наоборот. Данное условие необходимо, чтобы коэффициенты трансформации m, nТ были вещественными, в том числе и для произведений комплексных величин в формулах (5)–(8). В этом случае схемы на рис. 5, б и 6, б представляются в новом виде (см. рис. 9). Для первой дуальной пары схем на рис. 9, а, в коэффициенты трансформации m1 и m2, а также для второй дуальной пары схем на рис. 9, г, б коэффициенты трансформации m3 и m4 вычисляются следующим образом:

m 1(2)

= 1 -

² to

—

V^to x 1 ( 2 ) J

m 3(4)

= 1 -

^{2 to} x 1 ( 2 )

— to

V 7

где toxi(2) - характеристические частоты рассматриваемых на рис. 5, а и 6, а LC-цепей, которые определяются выражениями:

^to X i =

LC 1

to

x2 г ,

В выражениях (11) и (12) буквами C , C ₁ и L , L ₁ обозначены емкости и индуктивности, которые соответствуют сопротивлениям Z , Z ₁ и проводимостям Y , Y ₁ на рис. 5, а и 6, а . Из анализа полученных выражений (9)–(12) следует, что при использовании элементов цепей с реактивностями

разного знака можно на основе понижающего 1:(1/ m )-трансформатора реализовать устройство с функцией идеального повышающего трансформатора и, наоборот, применяя повышающий трансформатор 1: m , можно получить понижающее сопротивление устройство. Причем в том и другом случаях максимальная трансформация сопротивлений происходит на частотах ω , близких к характеристическим частотам to _x 1 и to _x 2 либо чуть меньшей для LC -цепей на рис. 9, а и в , либо чуть большей для LC -цепей на рис. 9, б и г . В отличие от следствия 1, второе следствие из-за отмеченной частотной зависимости коэффициентов трансформации в большей степени имеет отношение к процедуре относительно узкополосного согласования сопротивлений цепей. Рассмотренные на рис. 5, 6 и 9 повышающие и понижающие трансформаторы сопротивлений могут быть реализова-

ны в виде согласующих цепей с распределенными параметрами, если при этом применяются короткие по отношению к длине волны отрезки линий передачи [4]. Согласующие цепи на рис. 9, а также их распределенные аналоги широко используются, например, в литературе [14; 15].

Следствие 3. Понижающие сопротивления цепи с зависимыми от частоты коэффициентами трансформации можно комбинировать с понижающими сопротивление устройствами, в которых коэффициенты трансформации не зависят от частоты. Данное утверждение справедливо и по отношению к повышающим трансформаторам обоих типов. Например, если соединить друг с другом повышающие трансформаторы на рис. 6, в и 9, б , а также на рис. 6, г и 9, а , то получим повышающие согласующие цепи на рис. 10, а и б . Кроме того, если объединить вместе понижающие трансформаторы на рис. 9, в и 5, г и аналогичные устройства на рис. 9, г и 5, в , то реализуем комбинированные трансформирующие цепи, представленные на рис. 10, в и г соответственно. На рис. 10, а – г суммарные индуктивности L ^ и емкости С ^ находятся из выражений: L ₂ = L _с + L в и С ₂ = С с С в / ( С с + + C _B). Повышающие и понижающие сопротивления свойства таких комбинированных трансформаторов подтверждены в монографии [7] другим способом – с помощью использования метода крайних импедансов при анализе аналогичных относительно узкополосных согласующих цепей.

Таким образом, в данной работе при выполнении на основе теории фильтров широкополосного и узкополосного согласований импедансов в случаях с различными коэффициентами трансформации изучены особенности и следствия применения преобразований Нортона. Используя обобщенную форму записи преобразований Нортона при согласовании цепей с различными коэффициентами трансформации (больше и меньше единицы), отметили новую особенность 3 преобразований, обобщили следствие 1, а также установили характерные для узкополосных применений преобразований следствия 2 и 3. На основе следствий 2 и 3 синтезированы комбинированные повышающие и понижающие согласующие цепи.