Особенности расчета киральной среды в зависимости от концентрации киральных элементов

В настоящее время метаматериалы (греч. meta – «вне, за пределами»), т. е. композитные материалы с различными включениями, распределенными как хаотически, так и периодически, широко применяются, в частности, в радиотехнике, при конструировании космических аппаратов, в медицине и т. д. [1–4]. Благодаря этим включениям полученные материалы имеют многие полезные физические, электрические, оптические и другие свойства, которых нет у природных веществ. Среди метаматериалов выделяются вещества с киральными свойствами [5], которые способны вращать плоскость поляризации электромагнитных волн. В оптике аналогом подобных веществ служат оптически активные вещества, например кварц, раствор глюкозы и др. [6].

Однако методы расчета метаматериалов довольно ограничены [7]. В основном все расчеты базируются на решении уравнений Максвелла и подобранных в соответствии с задачей материальных уравнений.

Существующий подход обладает ограничениями, т. к. обычно используется при большой концентрации киральных включений, причем вводятся осредненные характеристики метаматериалов, например параметр киральности.

В настоящей работе сделана попытка более детального подхода к свойствам киральных метаматериалов. В частности, проведен анализ влияния этих свойств на взаимодействие киральных элементов индуктивного типа с электромагнитной волной, падающей на пластинку из метаматериала.

1. Линейный метод расчета взаимодействия метаматериала с электромагнитной волной

При исследовании метаматериалов с киральны-ми включениями на основе уравнений Максвелла обычно используют материальные уравнения, включающие т. н. параметр киральности % • В [8] предложены материальные уравнения в следующем виде:

D = б E + i ^Х H ,                                  (1)

a V

B = ц a H ± iV E ,                                 (2)

где D и B - индукции электрического и магнитного полей в электромагнитной волне, взаимодействующей с киральной средой; E и H - напряженности электрической и магнитной составляющей волны; б a и ц a - абсолютные электрическая и магнитная проницаемости киральной среды; V – скорость электромагнитной волны в киральной среде; х - параметр киральности, в данном случае безразмерная величина.

В [8] показано, что материальные уравнения (1) и (2) можно записать в следующем виде:

D = ( 1 ±х ) б a E ,                                      (3)

B = ( 1 ±х ) ц a H .                                    (4)

В формулах (1)–(4) верхние знаки относятся к правовращающему киральному элементу, нижние – к левовращающему.

Используя (3) и (4), можно показать [8], что, если киральная среда обладает только реактивными сопротивлениями, электромагнитная волна в ней подчиняется волновым уравнениям:

A D = Г 1 ±Х) ² d 2 D , I v ^J d t ²

A B = f 1 ±xf d 2 B ,

I V ^J d t ²

где t – время.

В дальнейшем нас будет интересовать только уравнение (5). Подставляя (3) в (5) и переходя к скалярному потенциалу ф [9], найдем:

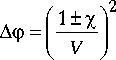
д2 ф д t2 "

Будем искать решение уравнения (7) в виде ф-ф ₀ =ф ( r ) exp ( i го t ) ,                              (8)

где ф о - начальный уровень отсчета потенциала; r – совокупность пространственных координат; го - циклическая частота падающей электромагнитной волны.

Подставляя (8) в (7), имеем:

Аф ( г ) + ( 1 ±х ) 2 к ² ф ( r ) = 0,

где к = ^ГО - модуль волнового вектора электромагнитной волны.

Решая уравнение (9), с использованием начальных и граничных условий можно исследовать процессы отражения, преломления, дифракции электромагнитной волны в метаматериале.

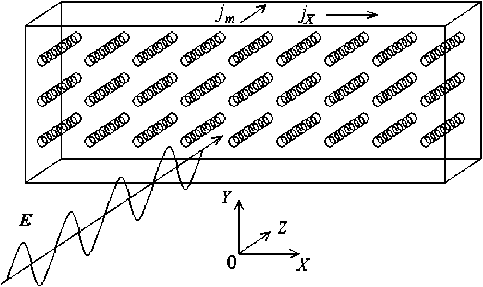
Рис. 1. Пластинка из метаматериала, облучаемая электромагнитной волной

Fig. 1. A plate of metamaterial irradiated by an electromagnetic wave

Особенностью пластинки является распределенная по ее поверхностям емкость при точечных индуктивных включениях. Поэтому рассматривать взаимодействие отдельного кирального элемента, имеющего индуктивность и емкость, с электромагнитной волной некорректно.

При облучении на пластинке возникает разность потенциалов, подчиняющаяся уравнению (7). Плотность тока через пластику будет иметь вид jm = Cm ^ + (ф-ф0 )gm, dt

где Ñm – емкость единицы площади пластинки; ф - потенциал на пластинке относительно исход- ного уровня фо; gm - электропроводность единицы площади пластинки за счет индуктивной составляющей.

Первое слагаемое (10) отражает емкостный ток смещения, второе слагаемое – индуктивный ток через киральные элементы.

Для спирального кирального элемента можно записать уравнение баланса напряжений:

d j.

-LiSi"^ = (ф-ф0), (11) д t где ji - плотность тока через i-й киральный элемент; Li - индуктивность i-го кирального элемента; Si – площадь пластинки, приходящаяся на один киральный элемент, имеющий индуктивную электропроводность gi.

Плотность тока ji через киральный элемент связана с разностью потенциалов на пластинке и электропроводностью этого кирального элемента gi по формуле закона Ома:

j i S i = g i ( ф ^- ф 0 ) .                                         ⁽¹²⁾

Подставляя (12) в (11), найдем:

g i =

(ф-ф0)

L ^ф i d t

Электропроводность, приходящаяся на единицу

пощади пластинки, равна:

gm

(ф-Фо)

SiLi

дф д t

Однако, учитывая, что продольный ток определяется только наличием поперечного тока (или наоборот), имеем:

где учтено g i = g m S i .

Подставив (14) в (10), найдем:

. дф ^(ф - ^ф 0 )

j = с ---.

m   m д t    _. дф

S i L i д t

Sdix = imbdx, где b – ширина однорядной пластинки.

Подставляя (21) в (22), имеем:

Используя C i = C m S i - емкость пластинки, приходящуюся на один киральный элемент, и обозна-

чая

ю =---

⁰ C i L i

– собственную частоту киральной

системы, найдем:

jm' - ( Ф-Ф о ) 2 “ 2 '                  «б

C m д t  ( д t )

Рассмотрим пластинку, состоящую из одного ряда киральных элементов, рис. 2.

Вдоль этой пластинки течет индуктивный ток.

Закон электромагнитной индукции для этого тока имеет вид

I

- L^-;^- = ^ф-ф 0 ,                              ⁽¹⁷⁾

S где Ix =Yx у(ф-Фо) — продольный индуктивный

ток; у x - удельная индуктивная электропроводность однорядной пластинки; L - ее индуктивность; S - площадь поперечного сечения однорядной пластинки; l – ее длина.

Следовательно:

дф

-Y XSL1   =ф-фо, д t

L где Li = -— индуктивность единицы длины одно рядной пластинки.

По закону Ома для плотности продольного тока имеем:

ix = "Г X *.                           «9

Следовательно:

d) x =-Y x ^ф dX '                         (20)

д X ²

Поделив (20) на (18) и сократив на у x , найдем:

di x =

ф-ф ₀ д ² ф

SL ₁

^д ф д X ² д t

dX .

jm

ф-ф ₀ д ² ф

L ₁

b ^дф д X¹² д t

Далее, подставляя (23) в (16), найдем:

ф-ф ₀ д ² ф

^C m L 1 b д XX-

дф ]             2 2

^f I ^-(ф-ф 0 ) “ 0 .

Учитывая С 1 = C m b - емкость единицы длины

однорядной пластинки и V ² = ^^ - квадрат ско-

рости электромагнитного поля вдоль пластинки,

имеем:

V ^(ф-ф 0 ) 2" = Гд?| ^-(ф-ф 0 ) “ 0 '            ⁽²⁵⁾

д x² I ^д t )

Нелинейное уравнение (25) можно преобразовать к виду, справедливому для пространственной геометрии:

V2Лф + “0(ф-ф0) =-----1 — I .

ф-ф ₀ (д t )

Линеаризацию уравнения (26) можно осуществить соотношением (8):

Лф(г) + к^ф( r ) = 0, где

, 2 _ “0 +“2 _ fc22

k s =    _о   = k 0 ⁺ k ,

V ²

где k_S – волновое число электромагнитной волны в киральной среде.

Заметим, что нелинейное уравнение, аналогичное (25) и (26), возникает при исследовании само-индуцированной прозрачности вещества [10], при распространении нервного импульса (последовательности потенциалов действия) по нервному волокну [11].

3. Различные виды решений уравнения взаимодействия метаматериала и электромагнитной волны

Линейные уравнения (9) и (27) отражают один и тот же физический процесс – распространение электромагнитных колебаний по киральной пластинке. Различие заключается в том, что при вы-

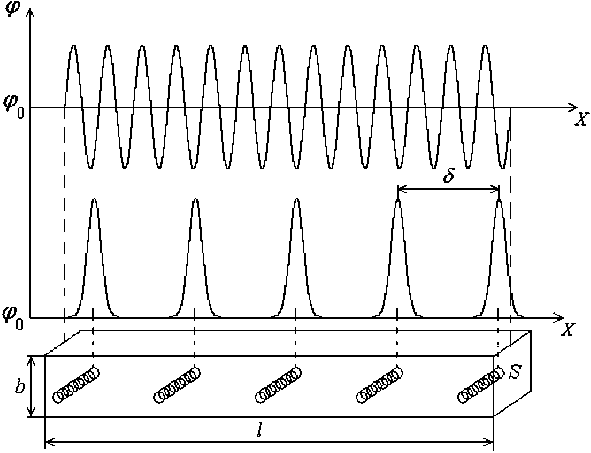
Рис. 2. Однорядная киральная пластинка

Fig. 2. Single row chiral plate

воде (27), в отличие от (9), не было необходимости использовать материальные уравнения (1)–(4), т. е. параметр киральности не вводился.

На основе тождества уравнений (27) и (9) можно положить:

к2 = k 0 + k ² = ( 1 + x ) ² к ² .                             (28)

В дальнейшем для определенности предполагаются правовращающие киральные элементы.

Следовательно, параметр киральности можно записать в виде

Х =

2?

А1 + Ч

N    к ²

- 1.

Если к о <<  к или to g << to (собственная частота киральной среды много меньше частоты падающей электромагнитной волны), то формула (29) упрощается:

к0

-----=

2 к 2

Заметим, что квантово-механический расчет оптически активного вещества [12] приводит к формуле для параметра киральности:

Х =

2 V n    ^to 0 j

,

3 ^п to ₀ j - to

где П - приведенная постоянная Планка; п — величина, пропорциональная произведению действительных частей электрического и магнитного дипольных моментов энергетического перехода оптически активной молекулы, возбуждаемого светом данной длины волны; to o j - в данном слу-

чае частота, соответствующая энергетическому переходу 0 ^ j [13].

Увеличение степени частотной зависимости to o до квадратичной в формуле (30) по сравнению с (31) является характерным при переходе из квантовой области в классическую.

На рис. 2 показан иллюстративный график колебаний потенциала на киральной пластинке в соответствии с колебательными решениями, удовлетворяющими уравнениям (9) и (27). Характер колебаний будет исследован ниже.

3.1. Многоволновое решение уравнения взаимодействия метаматериала и электромагнитной волны

Нелинейное уравнение (25) имеет по крайней мере еще одно решение в виде последовательности уединенных бегущих волн типа

Ф ^- Ф ₀ =

^Ф тах

exp

( ^k 0 ( X - X 0 ) ±to o ( t - 1 0 ) ) ² '

где к o = -^0 - волновое число собственной бегущей по киральной среде волны; Ф _тах - амплитудное значение потенциала Ф-Ф о ; X о - координата центра кирального элемента и, соответственно, максимума (центра) волнового импульса; t ₀ - время достижения этого максимума. Знак минус относится к волне, распространяющейся слева направо, знак плюс – справа налево.

Рост потенциала над киральными включениями, рис. 2, обусловлен пропорциональностью реактивного сопротивления киральных включений их индуктивностям ф —Ф о ~ Xy = to L i .

Из анализа обоих графиков можно заключить, что верхний график рис. 2 относится к достаточно частым включениям киральных элементов в пластинке, а нижний – к более редким. Поэтому вводить параметр киральности в решение (32) нерационально.

Очевидно, для нелинейных уравнений (25) или (26) должно существовать многоволновое решение. Многоволновые решения найдены для очень ограниченного круга нелинейных волновых уравнений [14; 15]. Многоволновое решение должно зависеть от концентрации киральных элементов в пластинке. Только с его помощью можно понять, при каких условиях можно обоснованно вводить параметр киральности, т. е. понять границы применимости материальных уравнений (1)–(4).

Уравнение (25) допускает многоволновое решение в виде

-to0 (t - t0n ))

N

+ kО Еф n n=1

и по времени t

дф д t

N

^-to 0 Е ^Ф n ⁽ k о ⁽ X - X 0 n ^)-to 0 ⁽ t ^- t 0 n ) ) , n = 1

подставим (36) и (37) в уравнение (34). Учитывая kоV = to0, получим:

Г N

Е ф n ( ^k о ( X - X 0 n ) -

V n = 1

N 7 N

^-to 0 ( t ^- t 0 n ) ) ⁺ Е ф n Е ф n = n = 1    7 n = 1

Еф n +

V n = 1    7

ЕФ n ( k о ( X - X 0 n )-to0

V n = 1

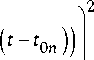
Ф = Ф о + Ф тах ^х

Г                                   хх2 7

( k 0 ⁽ X - X 0 n ) ^{- to} 0 ⁽ t - t 0 n ) )

V                                      7

N хЕ exp n=1

Сокращая в левой и правой частях (38) одинако-

Г N ) ²

вые слагаемые I Е Ф _n I , найдем:

V n = 1    7

где N – количество волн-импульсов, укладывающихся на длине l пластинки, рис. 2, равное количеству киральных элементов; n – текущий номер импульса; X _{0 n} – координаты максимумов волн-импульсов, t о n - времена достижения этих максимумов.

Подставляя (33) в (25), найдем:

NN           ₂

Е ф n Е ф n ( ^k 0 ( X ^- X О n )^-to 0 ( t ^- t О n ) ) = n = 1 n = 1

Е ф n ( ^k о ( X ^- X 0 n )^-to 0 ( t ^- t 0 n ) )

V n = 1

Рассмотрим два подряд идущих одинаковых импульса n = 1, 2. Записывая для этого случая формулу (39), найдем:

( - 2 A N        Г N

V ²14 Е ф n +- Е ф

Id X ² 7 n = 1         V n = 1

где обозначено:

Ф n = ^exP

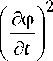
⁽ k о ⁽ X - X о n ) ^{- to} 0 ⁽ t ^- t о n ) ) 2

Находя производные по координате X

(ф1 + ф2) Vф1 (kо(X - X01)- to0 (t- t01)) ++ ф2 (k0 ( X - X02 ) - to0 ( t - t02= (Ф1 (k0 ( X - X01) - to0 (t - t01)) +

+ ф2 (k0 ( X - X02 ) - to0 ( t - t02

Преобразовывая формулу (40), получим:

2 N

• —7 = Е ^Ф n ⁽ k о ⁽ X ^- X 0 n ^)-

• дX   n=1

• ^-to 0 ⁽ t ^- t 0 n ) ) k О ^+Ф n k 0 =

= k О E Ф n ( k 0 ( X - X 0 n ) -                        (36)

n = 1

^k 0 ⁽ X 02 ^- X 01 ^)-to 0 ⁽ t 02 ^- t 01 ) = °. ⁽⁴¹⁾

Формула (41) указывает, что расстояние между киральными элементами 5 = ( X 02 - X 01 ) , рис. 2, электромагнитный импульс проходит за время ( 1 02 - 1 01 ) со скоростью V = to 0 / к о . Величина 1 / 5 характеризует линейную концентрацию кираль-ных элементов в пластинке.

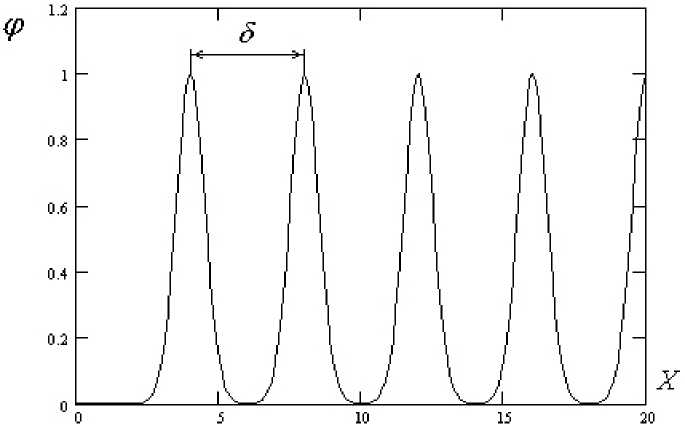
Рис. 3. Следующие друг за другом импульсы в многоволновом решении

Fig. 3. Consecutive impulses in a multiwave solution

Используя в (39) t 0 n = X 0 n I V = к 0 X 0 n I to ₀ , получаем, что выражения в скобках

( ^k 0 ⁽ X - X 0 n ) ^{- to} 0 ⁽ t - t 0 n ) ) = ( ^k 0 ⁽ X ) ^{— (to} 0 t ) )

не зависят от n , их можно вынести за знак суммы и сократить. В результате (39) превращается в тождество.

Следовательно, (33) является многоволновым решением нелинейного уравнения (25).

Наиболее простой вид многоволновое решение (33) приобретает в случае одинакового расстояния между всеми импульсами и, соответственно, между киральными элементами. В этом случае координаты максимумов импульсов X о n = n 5 , а времена достижения максимумов t о n = к о X о n / to o = = к о n 5 1 to o .

На рис. 3 для иллюстрации показаны несколько следующих друг за другом импульсов, построенных по формуле (33) при условиях: V = 0 - отсутствие зависимости от времени (фиксированная во времени картина), ф о = 0, Ф _шах = 1, к о = 2, 5 = 4.

Таким образом, формула (33) при условии равномерного распределения одинаковых импульсов является многоволновым периодическим решением нелинейного уравнения (25).

3.2. Решение уравнения взаимодействия метаматериала и электромагнитной волны в виде стоячих волн

Рассмотрим более подробно другой вид волны, возникающей на однорядной киральной пластинке при падении на нее электромагнитной волны.

Стоячие волны чаще всего образуются в линейных системах в результате суперпозиции (интер-

ференции) прямых и отраженных бегущих волн. Однако известно, что стоячие волны могут возникать и в нелинейных системах [16]. Многие физические процессы носят принципиально нелинейный характер, и процесс возникновения стоячих волн в таких системах нетривиален. Рассмотрим возможность возникновения стоячих волн в исследуемой киральной среде.

Нелинейные уравнения (25) и (26) можно решить методом Фурье разделения переменных [17]. Рассмотрим решение уравнения (25) в виде

ф-ф ₀ =ф ( X ) T ( t ) . (42) где ф ( X ) - функция только координаты Х ; T ( t ) -функция только времени t .

Подставив (42) в (25), найдем:

2 / \ 2/ \д²ф( X )

V2ф(X)T2 (t)---^ =

дX 2

( \ ^д T ( t ) ^           \          2

= ф ( X Ь^² -Ф ( X ) T ² ( t ) “ $ •

Разделим обе части уравнения на ф ² ( X ) T ² ( t ) .

В результате получим:

V ²

1 д ² ф ( X ) ф ( X ) д X ²

' 1 д т ( t ) ) ² . T ( t ) д t ,

+ ^to 0 =

-а ² .

где а - постоянная величина.

Уравнение (44) распадается на два независимых уравнения. Уравнение, зависящее от Х , имеет вид

Рис. 4. Переход многоволнового решения в решение в виде стоячей волны: 1 – многоволновое решение; 2 – стоячая волна Fig. 4. Transition of a multiwave solution to a standing wave solution: 1 – multiwave solution, 2 – standing wave

д0ф(X) Г 7 а21х

---+ к 0 +— ф( X ) = 0.                  (45) дX 2    ( а2

Сравнивая (45) и (27), замечаем, что ко = к0 +

1 о а Следовательно, к = —, и, значит, а = to .

V ²

Решение уравнения (45) запишем в виде

ф ( X ) = ф ( 0 ) exp ( ik s X ) ,                            (46)

где ф(0) - значение функции ф(X) в начале ко- ординат.

Второе уравнение равенства (44) имеет вид д T (t) • / х —= ito T(t).

д t

Решая это уравнение, найдем:

T ( t ) = T ( 0 ) exp ( i to t ) ,                                  (48)

где T ( 0 ) - начальное значение функции T ( t ) .

Используя (42), (46) и (48), найдем решение уравнения (25) в виде ф-ф0 =фд exp(itot)exp(iksX), (49) где обозначено фA = T(0)ф(0) - амплитудное значение потенциала ф-ф0 на пластинке

Функция ф-ф0 не должна иметь мнимых слагаемых, потенциал - величина действительная. Использование экспонент с мнимыми показателями вводится для удобства преобразований. Реально в этих экспонентах нужно учитывать только действительные слагаемые. Поэтому формула (49) описывает решение уравнения (25) в виде стоячих волн:

ф-ф0 = фд cos tot cosksX = пX

= ф_А cos to t cos----, ^д          5

где ф a - амплитудное значение стоячих волн; 5 -длина волны.

Условие возникновения узлов в стоячей волне – X _уз = ± ( 2 n + 1 ) 5 / 4, где n = 0,1, 2,...

На концах однорядной киральной пластинки, рис. 2, должны быть узлы стоячей волны. Если возбуждение волны происходит в центре пластинки, то номер максимально удаленного от центра пластинки узла можно найти по формуле

±—= ±(2п   + 1)— или п =

₂      n _{max    4}или n _max

Г I - 1 1

I 5 0 J

Нужно отметить, что бегущие волны ф-ф 0 =

2 . 2

ф                                    to +to

= д^-cos(ksX±tot) с учетом ks = 0 2— не являются решением уравнения (25), поэтому форму- лу (50) с физической точки зрения нельзя представить как сумму прямой и отраженной от границ пластинки волн, хотя математически эту процедуру несложно сделать. Это следствие нелинейности уравнения (25).

В заключение интересно проследить графически переход многоволнового решения (33) в решение в виде стоячих волн (50). Этот переход осуществляется при сближении импульсов, рис. 2, 3, т. е. при уменьшении величины 5 .

На рис. 4 показаны два графика. График 1 построен по формуле (33) при условиях: V = 0, ф 0 = 0, ф _max = 1, к 0 = 0, 5 = 0 для N = 8 импульсов.

График 2 (пунктиром) построен по формуле (50) при условиях ф о = 0,65 и ф д cos to t = 0,38 для некоторого момента времени t .

Заключение

Распределение потенциала на пластинке из метаматериала с индуктивными киральными включениями исследовано как с использованием материальных уравнений совместно с уравнениями Максвелла, так и на основе детального метода расчета взаимодействия киральных элементов и электромагнитной волны. Сравнение двух подходов позволило выяснить, что введение параметра киральности корректно только при достаточно высокой концентрации киральных включений. На основе сравнения результатов двух методов найдена частотная зависимость параметра ки-ральности. При использовании детального метода расчета взаимодействия киральных элементов и электромагнитной волны получено нелинейное уравнение для потенциала на пластинке из метаматериала, имеющее решения в виде стоячих волн и уединенных волн. Бегущие синусоидальные волны не являются решением этого уравнения. Показано существование многоволнового решения нелинейного уравнения. При уменьшении расстояния между киральными элементами исследован процесс перехода многоволнового решения нелинейного уравнения в решение в виде стоячей волны.