Особенности расчета рабочих параметров гибридных гидравлических систем с магнитожидкостными управляющими элементами

Объемы магнитных жидкостей уже давно применяются в качестве уплотнений и запорных элементов. В основном это связано с их адаптивностью, высокой точностью перекрытия сечения, долговечностью, надежностью и простотой реализации управления рабочими характеристиками в реальном времени. Поэтому данная технология считается перспективной для совершенствования и развития. Применение магнитожидкостных регулирующих элементов повышает энергоэффективность гидравлических систем, так как они не требуют энергетических затрат на перекрытие потока и при отключении управляющего электромагнитного поля магнитожидкостный регулирующий элемент возвращается к исходной геометрии, закрывая регулируемую им гидролинию.

Актуальность

Гибридные гидравлические системы позволяют сократить расход электроэнергии по сравнению с классическими гидравлическими аналогами. При этом системы с магнитожидкостными регулирующими элементами обладают высокой точностью и скоростью отработки управляющего сигнала. Поэтому развитие магнитожидкостных технологий является актуальным.

Фундаментальные основы расчета магнитожидкостных управляющих элементов

Сферический объем магнитной жидкости, помещенный во внешние магнитные поля, трансформируется и приобретает эллиптическую форму (рис. 1), при этом происходит вытягивание объема в направлении действия напряженности магнитного поля и сжатие в направлении, пер- пендикулярном направлению действия магнитного поля [1].

Параметры получающегося эллипсоида: длинная полуось: b = R + db;

короткая полуось:

а = R — da.

Так как объем магнитной среды постоянен справедливо следующее:

(4^/3)R³ = (4^/3)(R + db)(R — da)² = V, R - радиус сферического объема, V - объем магнитореологической жидкости:

V = 4яаЬ2/3.

Где напряженность размагничивающего магнитного поля, внутри сферического объема магнитной жидкости (противоположного по направлению внешнему магнитному полю):

Н = Н0 — (N/^0)M(H),

М - намагниченность, Н_о - внешнее магнитное поле, ^_о - магнитная проницаемость вакуума, N - размагничивающий фактор:

N = —— [ ^— ln(n + Vn2 — 1) — 1], n2-1 Vn2-1

n = b/a.

Суммарная магнитная энергия магнитной жидкости выражается, как:

umas = — Vj^(H')dH'.

Магнитная сила, возникшая в результате деформации объема:

F = — аи^ = v^_ f^H M(H ' )dH ' . db db О

Уравнение Бернулли для магнитной жидкости:

(1/2)pv2 + pgz + р JO M(H') dH' = const,

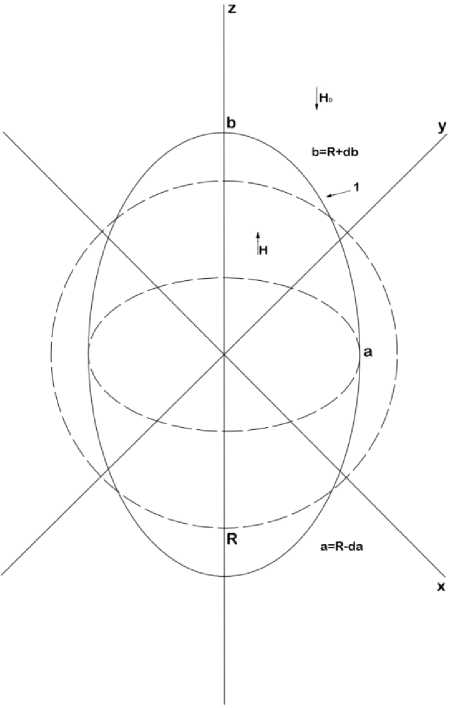
Рис. 1. Трансформация сферического объема магнитной жидкости в эллипсоид вращения: 1 – объем магнитной жидкости

р - давление в магнитной жидкости, p - плотность, g - ускорение свободного падения, v -

скорость, z - высота по нормали.

Прикладной расчет магнитожидкостных управляющих элементов

Описание рабочего процесса магнитожидкостного управляющего элемента требует рассмотрения воздействия на стенки упругого элемента, заполненного магнитной жидкостью, магнитной и немагнитной сред.

Сделаем допущение о том, что наличием тонкой стенки упругого элемента можно пренебречь.

Поэтому равновесное давление на границе раздела (на стенке упругого элемента, заполненного магнитной жидкостью) со сторон магнитной и немагнитной сред выражается как [1-3]:

Pb = Ра + Ома(Ю dH + -^М2П, о                   2Мо рь - давление со стороны немагнитной жидкости, ра - давление со стороны магнитной жидкости, Мап - нормальная компанента намагниченности:

МаП = Ма^П.

Физические величины с индексом а относятся к магнитной среде.

Для осей симметрии эллиптического объема магнитной жидкости равновесные давления на стенку примут следующие значения.

Расчет и конструирование

Ось симметрии, длинная полуось при М_ап = М_а :

Рь(ОВ) = Ра(ОВ) + СН“Ма(Я) dH + 1-М2.

^о                   z^ o

Ось симметрии, короткая полуось при М_ап = 0:

рь(ОА) = Ра(ОА) + /0Н“Ма(Н) dH,

Сферическая форма небольшого объема магнитной жидкости физически более предпочтительна и связана с капиллярными эффектами, В случае попадания объема магнитной жидкости в направленное внешнее магнитное поле создается разность давлений на осях симметрии сферического объема, в результате чего происходит трансформация формы объема, приобретение эллиптической формы, компенсация неоднородности давления внутри объема магнитной жидкости вследствие нарастания кривизны поверхности и роста капиллярного скачка давления,

Форму объема магнитной жидкости во внешнем магнитном поле можно выразить из условия минимума суммы магнитной энергии:

E = итад + Es,

E_s - поверхностная энергия:

Es = 2луаЬ[1/к + (1/e)arcsine], у - коэффицент поверхностного натяжения, е - эксцентриситет эллипсойда:

е = ^(а2 — b2^/a,

Плотность потока энергии (вектор Пойнтинга) [4-8]:

п= £[EH],

4л

E - напряженность электрического поля [9-10]:

F

E = 7,

F_q - сила, действующая на заряд, q - заряд, с - скорость распространения электромагнитных взаимодействий в вакууме:

с = 3 • 1010см/с.

Справедливо следующее:

- [EH] = -,

4л          St’ t - время, 5 - площадь сечения переноса энергии,

Электромагнитная сила [11-12]:

Fei = ВИ, i - сила тока, I - длина проводника, В - магнитная индукция поля:

В = р0(Н + М),

Электромагнитная сила с учетом характеристик индуктора:

Fel = (Nn • О2 • Во • 5т/(2 • ^тгХ

1_т - длина зазора между индуктором объемом магнитной жидкости, 5_т - площадь сечения электромагнита, N_n - количество витков,

Оптимальные режимы работы магнитожидкостных элементов можно достичь при их эксплуатации на малых значениях сечений радиальных зазоров, поэтому расход жидкости на магнитожидкостном элементе [13-20]:

„ = Ьрла _о б р

• ^— 2pl-10^s ’

• 5₀ - радиальный зазор, Др - перепад давления в зазоре, d₀ - средний диаметр магнитожидкостного элемента, в - вязкость среды, I - длина магнитожидкостного элемента,

Применения магнитожидкостных управляющих элементов и оригинальное конструктивное решение гибридного гидравлического аппарата

Использование нестационарных электромагнитных полей, рационально в гибридных гидравлических аппаратах, На рис, 2 представлен гибридный гидравлический аппарат, имеющий в своей конструкции магнитожидкостные регулирующие элементы [21],

В предложенной конструкции регулирование расходных характеристик магнитожидкостных элементов реализуется посредством изменения вольт-амперных характеристик, частоты и длительности электрических сигналов, подаваемых на электромагниты и синхронизации / рассинхронизации управляющих сигналов открытия / закрытия магнитожидкостных регулирующих элементов относительно друг друга,

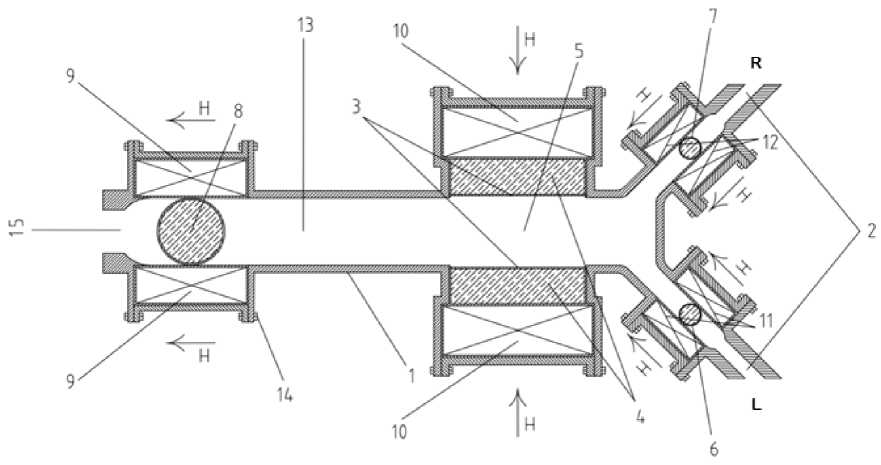
Рис. 2. Смеситель – дозатор с магнитожидкостными управляющими элементами: 1 – корпус, 2 – подводящий канал, заполненный компонентом смеси, 3 – мембрана, 4 – кольцевая полость, заполненная магнитной жидкостью, 5 – рабочая камера, 6, 7, 8 – магнитожидкостный клапан, упругая сферическая капсула, заполненная магнитной жидкостью, 9, 10, 11, 12 – кольцевой электромагнит, 13 – напорный канал, заполненный смесью, 14 – крепежный элемент, 15 – канал подачи готовой смеси, H – направленное электромагнитное поле

Смеситель – дозатор с магнитожидкостными управляющими элементами – работает по принципу создания перепадов давления в рабочей камере посредствам изменения электромагнитной составляющей давления в магнитной жидкости, находящейся в полости, отделенной от рабочей камеры упругой мембраной. При импульсной подачи напряжения на кольцевой электромагнит, управляющий полостью, заполненной магнитной жидкостью, в магнитной жидкости происходит высокочастотная пульсация электромагнитного давления, являющегося составной частью полного давления, оказываемого на мембрану со стороны магнитной жидкости. Это приводит к передаче пульсации давления через мембрану в рабочую камеру смесителя – дозатора. Значение перепада давления в рабочей камере регулируется посредством управления нагрузкой, подаваемой на кольцевой электромагнит, управляющий полостью, заполненной магнитной жидкостью. Расход смеси и компонентов регулируется при помощи магнитожидкостных элементов, помещенных в электромагнитные управляющие поля. Степень открытия магнитожидкостных клапанов управляется за счет изменения мощности кольцевых электромагнитов в зонах, действия которых размещены соответствующие магнитожидкостные элементы. Сферические объемы магнитной жидкости имеют свойство в направленном магнитном поле принимать эллипсоидальную форму. Поэтому упругие капсулы, заполненные магнитной жидкостью, находящиеся во внешнем магнитном поле, вытягиваются в направлении действия приложенного внешнего магнитного поля и сжимаются в направлении, перпендикулярном магнитному полю. Приобретая эллипсоидальную форму, магнитожидкостные элементы изменяют пропускную способность каналов, в которых они размещены. Поэтому направление действия магнитного поля электромагнита, управляющего полостью, заполненной магнитной жидкостью перпендикулярно направлению тока смеси в рабочей камере, а направление действия магнитного поля электромагнитов, управляющих магнитожидкостными элементами параллельно направлению тока компонентов и смеси в каналах. Высокочастотная пульсация давления в рабочей камере приводит к перемешиванию компонентов.

Целесообразно выполнение мест под посадку магнитожидкостных элементов в виде каналов с расширениями, образующими полости. Подобная геометрия проточной части обеспечивает са-могерметизацию магнитожидкостных регулирующих элементов и расширяет интервал рабочих давлений.