Особенности распределения плотности связанной жидкости в капиллярно-пористых средах

ОСОБЕННОСТИ РАСПРЕДЕЛЕНИЯ ПЛОТНОСТИ

СВЯЗАННОЙ ЖИДКОСТИ В КАПИЛЛЯРНО-ПОРИСТЫХ СРЕДАХ

В. Б. Заалишвили, Т. Р. Тедеев, К. С. Харебов

В данной работе получены аналитические зависимости, позволяющие прогнозироватв колебания плотности на всем интервале изменения связанной жидкости. Разработанная методика учитывает особенности структурных разновидностей поровой влаги. Проведен сравнительный анализ полученных резулвтатов с экспериментальными данными других авторов.

Известно [4], что методика определения плотности связанной воды, которая сравнительно больше свободной, требует дальнейшего совершенствования. Немногочисленные экспериментальные и теоретические исследования [2, 3] носят противоречивый и незаконченный характер.

Рассмотрим некоторый объем капиллярно-пористой среды. При массе скелета среды тд, объем будет равен

=                                      (1)

Ра а для объема твердых частиц среды имеем

V_s =                                         (2)

Ps где рд — плотность скелета пористой среды; ps — плотность твердых частиц пористой среды.

Предположим, что в порах среды содержится вода, величина (количество) которой соответствует максимальной молекулярной влагоемкости

^Уттш

= w_mw + И©„ + W_dw,

где lT_mw — влага монослойной адсорбции, W_pw — влага полислойной адсорбции, W_dw — диффузионная влажность.

Суммарный объем жидкости в среде будет составлять nw

— ^mw

+ Tlpw

+ ndw.

Представим объем твердого компонента вместе с жидкой в следующем ви де

Cs = —+

Ps

mmw

Pmw

+

^pw Ppw

mdw

Pdw

^где Pmw — плотность мономолекулярной влаги, p_pw — плотность полимолеку-лярной влаги, p_dw — плотность диффузионной влаги.

Соотношение (5) можно переписать в другом виде:

Vs = md	" 1	1	mmw	1 + — Ps	трги	1 + — Ps	mdw"	(6)
	.Ps	Pmw	md		md		md

Заметим, что величина V_s из зависимости (6) не является контракционным объемом капиллярно-пористой среды [1].

Величину влагосодержания среды будем оценивать по верхнему пределу полимолекулярной адсорбции

Hw

W

V^mpw

т. е. если H_w = 1, то влажность среды будет W = W_mpw.

Зависимость (7) можно переписать в развернутом виде:

fmw\Aw = н mw\™P™

Vm_d) ^w X m_d )

I

Нижний предел влагосодержания среды представим следующим образом:

(m™\^Aw₌ _ rm_w\m_Pw ^w X тд /

I

Если считать, что Н^ — нижняя граница влагосодержания, a p^ — плотность воды при этой влажности, то для влажности мономолекулярной адсорбции можно написать равенство

H_w /m_w\mpw = н^ /m_w\ p(H_w)\m_d)     Piw^m_d)

mpw Ц^

^^^^^^^^.

IT ги

Pmw

С т„ \^mpw х m_d )

или преобразованием можно получить

Hw

Hw

Р^Н^

^^^^^^^^™

H'

Ш

Pmw

Pmw

(

Piw

^^^^^^^^™

Pmw

Piw

)■

После того, как мы вынесем общий множитель -^— за скобки, получим Pmw

Hw

P^H^

Pmw L

Hw

^^^^^^^^™

я:(

^^^^^^^^™

Pmw

Piw

)]■

Для влажности монослойной адсорбции окончательно можно написать рЛч") =

HwPmw

Hw

^^^^^^^^^

Щ(1

^^^^^^^^^

m w

Pi w

)

или с учетом зависимости (7) имеем где W^

Р(ИЗ =

плотность при H_w

H^ Pmw

W

^^^^^^^^™

п(

^^^^^^^^™

Pi w

)

= Н

1J-IW

В интервале полимолекулярной адсорбции Н™ < H_w< Н^, равенство (10)

можно представить в следующем виде

Hw

p(Hw)

IP

= — +

Hm w

^^^^^^^^™

IP

Piw

Pmw

+

Hw

^^^^^^^^™

H^m w

Ppm

или после некоторых преобразований имеем

Hw p(Hw)

тт TTi Ppw ( 1

Pmw '

Pmw Piw

^^^^^^^^™

nm

(*-

Ppw

Pmw

)

Окончательно зависимость для определения плотности в интервале полис-лойной адсорбции имеет вид

Нго Ppw

h_w -        (1 -     - Н™ f 1 -

W     w Pmw \ Piw /     w \ Pmw / или через влажность пористой среды

P(W) =

_______________ Wp_pгo _______________

W - ИД-^fl -    - Ж™ fl - w Pmw \ Piw / w \ Pmw /

На интервале диффузионной влажности Н^ < Hw < H^w для определения зависимости плотности от влажности можно составить равенство

Н    Hi нт -IP нр - нт н — нр p(Hw) Piw     Pmw        Ppm        Pdw (19) или после некоторых преобразований, получим

H               № Г    л 1     Ит Г     л 1       Г    л , 1 L1w _                             j    Ppw    др j pdw p(Hd)   Pdw Pmw .    Piw .    Ppw .    Pmw.       .    Ppw.

(20)

Вынося величину -^— за общие скобки, имеем Pdw

Hw _   1 J    _ тгг Pdw . _ Pmw ( TT \              )                in           1 P\^w) Pdw I          Pmw L     Piw _     Pdw 1 _ Ppw _ тур 1 _ Pdw 1 w                             W               | ■ Ppw L Pmw J       L Ppw J J

(21)

Окончательно для диффузионного интервала изменения влажности зависимость плотности от влажности имеет вид

= -------------7-------у---HwPdW zу------7-------x- H - Ш рд™ (1 - p™™ 1 - Hmi^( 1 - Ррш \ - НРИ - 2^ 1 w     w Pmw \     Pi w /     w Ppw \    Pm w /       \    Ppw / (22) или с учетом зависимости (7)

/>(1V) =------------?x? W - Ж(,^ 1 - ^ - Ж™^ 1 - ^ _ ppp 1 _ Щ- Pmw \     Piw )     ^ Ppw \    Pmw /        \    Ppw /

(23)

В первом приближении для ориентировочных расчетов, при условии, что нижний предел влагосодержания находится в интервале полислойной адсорбции, можно составить следующее упрощенное равенство

Hw   Hp Hw- Hp p(Hw)   pp      pw (24) где Pw — плотность воды р = 1г/см3.

Из равенства (24) преобразованием можно получить

Hw _HP Нрд pw\ P(Hw) Pp   Pw     Pp/

(25)

Окончательно зависимость для плотности связанной воды имеет вид

p(Hw) =

-И W Pw

или учитывая зависимость (7) можно написать

Wpw

w-wp^-^y

На основе разработанной методики рассмотрим модельную задачу определения плотности в зависимости от влажности (рис. 1).

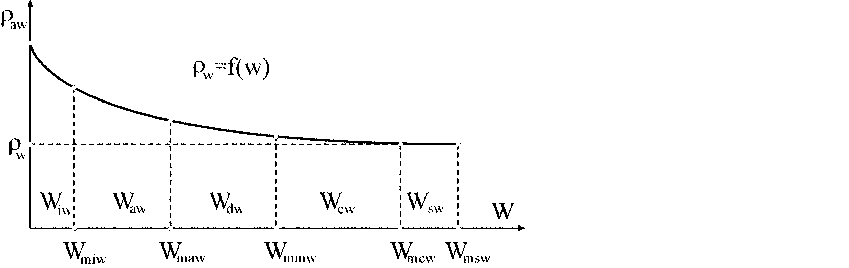
Рис. 1. Условная кривая изменения плотности связанной воды пористой среды

Для ориентировочных расчетов выделим три характерных интервала изменения влажности: интервал монослойной адсорбции Н^у < Hw < Н^ ₁ интервал полислойной адсобции Н^ < Hw < Н^ и интервал диффузионной влажности Нуу < Hw < Нуу. Примем на интервале монослойной адсорбции следующие расчетные значения плотности — piw = 1.8г/см³, Pmw = 1.44г/см³, в качестве верхней границы интервала полислойной адсорбции имеем — ppw = 1.2г/см³, для диффузионного интервала будем считать, что paw = Pw = 1г/см³. На исследуемом интервале Нуу < Hw < Нуу функцию влагосодержания будем оценивать по величине относительной упругости водяного пара P/Ps- Для сравнения полученных результатов приведем экспериментальные данные Кульчицкого Л. И. из [3], см. таблицу 1.

Таблица 1

Результаты эксперимента по величине P/Ps

P/Ps 0.01 0.05 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.98

1.80 1.51 1.44 1.38 1.31 1.30 1.29 1.29 1.31 1.30 1.29 1.2

Результаты расчетов авторов по величине Hw

Hw 0.01 0.05 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

р(НД 1.80 1.48 1.45 1.31 1.27 1.25 1.24 1.24 1.23 1.23 1.22 1.22

При этом согласно зависимости (13) для первого интервала имеем p(Hw) = Hw • 1.44/(Hw — 0.002), второй интервал согласно (17) характеризуется p(Hw) = Hw • l-^/^Hw — 0.017) и для диффузионного интервала из зависимости (22) получается p(Hw) = Hw/^Hw ^- 0.181). Результаты расчета приведены в таблице 1.

Анализ зависимостей (10)—(23) позволяет сделать следующие выводы:

• 1.    Полученные аналитические зависимости позволяют прогнозировать колебания плотности на всем интервале изменения связанной влаги и в то же время сравнительно просты для применения в расчетах.

• 2.    Преимущество разработанной методики заключается в учете особенностей структурных разновидностей поровой влаги.

• 3.    Результаты сравнительного расчета по поставленной задаче показали, что расхождение с данными эксперимента составляет 2 5%.