Особенности распространения волн Лява в упругих функционально-градиентных покрытиях

Применение новых наукоемких и высокотехнологичных функционально-ориентированных материалов в различных отраслях, от космических технологий, медицины до производства строительных материалов и конструкций, приводит к необходимости прогнозирования изменения физических, технологических и прочностных качеств используемых материалов в зависимости от условий эксплуатации и характера

внешних воздействий. Сложность возникающих при этом динамических задач состоит в том, что для полуограниченных сред с изменяющимися в пространстве свойствами или структур с покрытием из подобных материалов аналитическое решение получить невозможно. Достаточно распространенное в литературе предположение о том, что все свойства материала изменяются по одной пространственной переменной с одинаковой интенсивностью и одному закону [1-9], приводит к существенному упрощению задачи. При моделировании функционально-градиентного материала часто прибегают к делению на слоистые элементы, в которых свойства материала являются линейными [7] или квадратичными функциями толщины, а в качестве зависимостей изменения свойств используют легко дифференцируемые функции и многочлены [3, 5, 6]. В [9] выбирались участки с однородными свойствами и участки с их непрерывным изменением, при этом непрерывная зависимость по толщине задавалась гладкими функциями, связывающими значения скоростей объемных волн и плотности на соседних участках однородности. В качестве гладких функций в работе взяты кубические сплайны, обеспечивающие непрерывность функций и их первых производных.

Как правило, в моделях рассматривается трансформация свойств либо относительно одного «опорного» материала, либо двух [4,8]. Предположение об идентичности изменения всех свойств материала позволяет получить аналитическое решение, что важно при оценке результатов применения более сложных численных и численно-аналитических методов, но при исследовании свойств реальных материалов эффективно только в отдельных частных случаях. Ранее в [10] предложена, а в [11-15] усовершенствована численно-аналитическая модель функционально-градиентной среды. В ее основе лежит сведение решения уравнений движения — системы дифференциальных уравнений в частных производных 2-го порядка с переменными коэффициентами, к решению системы обыкновенных дифференциальных уравнений (ОДУ) 1-го порядка с краевыми и начально-краевыми условиями относительно компонент вектора перемещений и нормальных компонент вектора напряжений. В свою очередь решение системы ОДУ с переменными коэффициентами строится численными методами. Такой подход к моделированию функционально-градиентных покрытий и сред с их наличием позволяет учитывать различия в законах и интенсивности изменения свойств материала. В [14] возможности метода проиллюстрированы на широком круге динамических задач для упругих и электроупругих сред с неоднородными как слоистыми, так и функционально-градиентными покрытиями. Вопрос об особенностях структуры волнового поля самого покрытия не рассматривался. В [15] на примере слоя с немонотонной трансформацией свойств показано распределение амплитуды и фазы смещений по толщине для различных частот колебаний.

В настоящей работе проведен анализ влияния интенсивности, характера и области локализации неоднородности изменения свойств покрытия на структуру поверхностного волнового поля. Исследованы случаи «акустически однородных и неоднородных» покрытий с монотонным преобразованием свойств. Установлено, что «акустически однородные» покрытия с различным типом неоднородности и областью ее локализации при равных дисперсионных свойствах различаются интегральными характеристиками, в частности, смещением в отдельных модах поверхностных волн, и совокупным смещением каждой точки поверхности. Показана возможность управления резонансными эффектами — сдвигом резонансных частот, ростом или подавлением амплитуды смещения поверхности вне резонансных областей, за счет целенаправленного варьирования свойств материала покрытия.

2.    Постановка задачи

В декартовой прямоугольной системе координат O x 1 x ₂ x ₃ рассматривается задача об установившихся гармонических колебаниях неоднородной среды под действием нагрузки q = { q 1 , q ₂ , q ₃ } e ^- i ™ t , распределенной в области Q ее поверхности. Среда представляет собой слой | x j, | x ₂ |<да , 0 <  x ₃ <  h , нижняя грань которого защемлена; упругие параметры Х ( x ₃ ), ц ( x ₃ ) и плотность р ( x ₃ ) предполагаются произвольными, достаточно гладкими функциями координаты x ₃ . С учетом характера движения среды, все параметры задачи представляются в виде ( ю — угловая частота):

f ( x , x 2 , x 3 , t ) = f ( x p x 2 , x 3 ) e ^- i ^ю t .

Далее временной множитель опускается.

Краевая задача о колебаниях неоднородного слоя описывается уравнениями движения

• V- 0 = —рю ² u                                       (1)

с граничными условиями x3 = h :     n ■ 0 = q, x1, x2 e Q, n ■ 0 = 0, x1, x2 г Q;

x ₃ = 0:      . = 0.

Здесь: . = {u 1 ,u ₂ , u ₃} — вектор перемещений произвольной точки слоя; 0 — тензор напряжений; n — вектор нормали.

Компоненты тензора 0 представляются формулой

® lk    ^X Iksp u s , p '

где X _lksp — упругие константы, определяющие закон состояния слоя, которые для изотропной среды имеют вид [10, 14] ( 5 ks — символ Кронекера):

X lksp = ( 5 is 5 kp +5 ks 5 p ) ц + 5 ik 5 sp X .                                            (4)

Полагаем, что свойства материала слоя изменяются по толщине:

р ( x 3 ) = Р о f , ( x 3 ) , ц ( x 3 ) = P o f . ( x 3 ) , ^X ( x 3 ) = ^X 0 f Л x 3 ) ,                            ⁽⁵⁾

где функции f _р ( x ₃ ) , f ₁( x ₃ ) , f _x ( x ₃ ) определяют поведение соответствующих параметров, р ₀ , X ₀ , ц ₀ — плотность и модули некоторого «опорного» материала, в качестве которого использован упругий изотропный материал, закон состояния которого описывается соотношением (4).

Перейдем к безразмерным параметрам (далее штрихи опущены):

ц' = ц/ц0,    X' = X/X0,    Р' = Р/Р0,    l ' = l/h,    to = hto/ Vs,

где l — линейный размер, V S ⁰ = ^ц ₀ /р₀ — скорость сдвиговой волны «опорного» материала.

Особенность краевой задачи (1), (2) состоит в том, что коэффициенты в уравнении движения (1) являются функциями координаты x ₃ .

3.    Сведение к задаче Коши

Применив к уравнению (1) двумерное преобразование Фурье по координатам x 1 и x ₂ ( а 1 , а ₂ — параметры преобразования), представим его в виде [14]

Y ‘ = M ( а 1 , а ₂ , x ₃ ) Y ,

Y=|Л Y     ( 3 *lk=1- Y =1 l^kl.=1,V 7

здесь U k , 0 _{3 k} — трансформанты Фурье компонент вектора перемещений и тензора напряжений (3). Матрица M ( а 1 , а ₂ , x ₃ ) имеет вид:

	( 0	0	i а 1 Х	P 1
			X + 2 ц
	0 i а 1	0 i а 2	i а 2 X X + 2 ц 0	ц ( 3 X + 2 ц ) а,а2—------- 1 2 X + 2 ц 0
M =	1	0	0	0
	ц 0	1	0	0
	0	ц 0	1	i а 1 X

X + 2 ц

X + 2 ц

ц ( 3 X + 2 ц ) а.а2—------- 1 2 X + 2 ц	) 0
P 2	0
0	-рю 2
0	i а 1

i а2X

X + 2ц

'

P 1 = 4 ца 2 ——— + ца 2 -рю ² , Р ₂ = ца 2 + 4 ца 2 —— --рю ² .                (9)

Х + 2 ц                            Х + 2 ц

Вектор Y (7) формируется из компонент вектора напряжений и перемещений, что дает возможность обойтись без производных в матрице M ( а 1 , а ₂ , x ₃ ) Последнее обстоятельство позволяет существенно расширить класс функций, описывающих закон изменения параметров среды, и, в частности, использовать кусочно-непрерывные функции.

• 3.1.    Функция Грина функционально-градиентного слоя

Уравнение (6) в обозначениях (7)-(9) представляет собой систему линейных дифференциальных уравнений с переменными коэффициентами, решение которой строится на основе численного решения набора задач Коши для уравнения (6) с начальными условиями при фиксированных значениях параметров а 1 , а ₂ . Для решения системы (6)-(9) применяются различные подходы и численные схемы [4, 7-9, 16, 17], в настоящей работе при построении функции Грина использована модификация численного метода Рунге-Кутты.

Пусть у_кт ( а 1 , а ₂ , x ₃ ) ( т , к = 1,2,...,6) — набор линейно независимых решений уравнения (6) с начальными условиями:

У кт ( ^а 1 , ^а 2 ^,0 ) = 5 кт .                                              ⁽¹⁰⁾

Общее решение для слоя с переменными свойствами имеет вид:

Y k = £ С т ( « 1 , а 2 ) У кт (а_р а ₂ , x 3 ) ( к = L²,.., 6),                           (1¹)

т = 1

где неизвестные коэффициенты с_к ( а 1 , а ₂ ) определяются при удовлетворении граничных условий:

D ( а 1 , а ₂ , x ₃ ) Y = Q .

В случае слоя с защемленным основанием

D = E ,      Q =t { Q 1 , Q ₂ , Q 3 , 0,0,0 } .

Здесь E — единичная матрица. После внесения представлений (11) в (12) и учета условия (13) получим систему линейных алгебраических уравнений относительно вектора c =Т { с_к } 6 = 1

R ■ c = Q

с матрицей R размером 6 х 6:

R km = У кт К а 2 , h ) ( к = 1,2,3, т = 1,2,..., 6);

R km = У кт ( а_Р а ₂ ,0 ) ( к = 4,5,6, т = 1,2,..., 6).

Используя обратное преобразование Фурье, с учетом обозначений (7) запишем решение краевой задачи (1) и (2) в виде:

u ( x 1 , x 2 , x 3 ) = -^j" Jk ( x -^ , x 2 -n , x 3 ) q ( ^ , n ) d § d n , ^{4 n}

k(5,t,x3) = j j K(ара2,x3)e i(аs"‘)dа1 dа2,       K(ара2,x3) = ||k„,+3,я|т^ .,(17)

г, г”’"

Ктп = Л"‘ £ЛпкУтк (а1, а2, x3) ,      А = det R • к=1

Здесь A nk — алгебраическое дополнение элемента R nk матрицы R (14), (15). Контуры Г 1 и Г 2 в представлении (17) выбираются по правилам, указанным в [18]. Формулы (16)–(18) определяют перемещение произвольной точки слоя, выполненного из функционально-градиентного материала под действием заданной в области Q нагрузки.

Для исследования дисперсионных свойств структуры, поведения и скорости распространения поверхностных волн достаточно рассмотреть дисперсионное уравнение

A ( a 1 , a ₂ , to ) = 0 .

• 3.2.    Функция Грина функционально-градиентного слоя при сдвиговых колебаниях

При использовании предложенного подхода для исследования сдвиговых колебаний функциональноградиентного слоя, вызванных действием распределенного в области { Q ( x 1 ,x 2 ,x 3 ) : | x ] <  1,| x ₂| < « , x 3 = h } поверхностного источника, в краевой задаче (1), (2) необходимо учесть условия:

A = o.

d x ₂

u ₂ = u ₂ ( x 1 , x 3 ),     u 1 = u 3 = 0,

В сделанных предположениях, согласно (16)–(18), смещение слоя представляется выражениями:

u 2 ( x_vx 3 ) = — k 22 ( x 1 -^ , x 3 , to ) q ( ^ ) d § ,

2 n - 1

k ₂₂ ( 5 , x 3 , to ) = J K ₂₂ ( a , x 3 , to ) e - i “ s d a , K ₂₂ ( a , x 3 , to ) = y ₂₁ ( a , x 3 , to ) [ y 11 ( a , h , to ) ] 1 ;

Г a — параметр преобразования Фурье по координате x1. Контур Г выбирается в соответствии с условиями излучения [18]; как правило, он совпадает с вещественной осью и отклоняется от нее вверх при обходе отрицательных полюсов функции K22 и вниз — при обходе положительных. По аналогии с (10), yjk (a,x3, to) — линейно независимые решения задачи Коши с начальными условиями yjk (a,0, to) = 8 jk для уравнения

Y ' = M ( a , x 3 ) Y ,                                          (21)

здесь

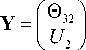
,     . Г 0      pa ² - pto'

M (“’ x3 ’-[(H)-      0

Представление (19) определяет смещение произвольной точки слоя, вклад в смещение поверхностных волн находится через вычеты в полюсах. В случае точечного источника колебания q ( x 1 ) = {0, 8 ( x 1 ), 0} (здесь 8 ( x 1 ) — функция Дирака) для смещения в слое справедливо выражение:

u ₂ ( x 1 , h , to ) = -^-J K ₂₂ ( a , h , to ) e i “ x ¹ d a .

Вклад мод поверхностных волн имеет вид:

u 2 ( x 1 , h , to ) = + i Res [ K ₂₂ ( a , h , to ) e - i “ x ¹ ]

4.    Численный анализ

В рамках предположений раздела 2.2 рассмотрим сдвиговые колебания слоя, вызванные действием поверхностного точечного источника. Свойства слоя меняются по толщине монотонным образом, функциональные зависимости f_s ( x ₃ ), участвующие в (5), приведены на рисунке 1. В качестве «опорного»

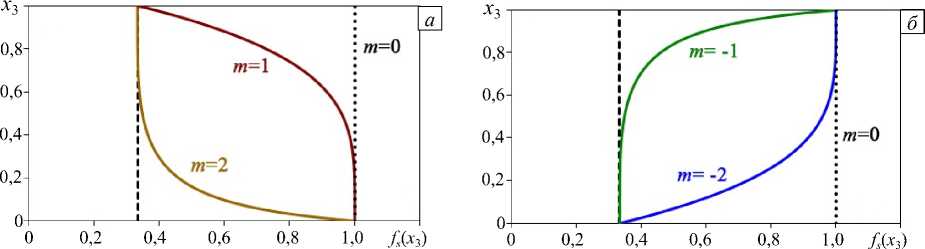
Рис. 1. Вид функциональных зависимостей при «нормальном» ( а ) и «аномальном» ( б ) изменении свойств слоя

использован изотропный материал с параметрами [10]: р ₀ = 7,748 - 10 3 кг/м³; ц ₀ = 0,804 - 10¹¹ Н/м²; Х ₀ = 1,1 - 10 11 Н/м².

На рисунке 1 и далее индексом « m » отмечены различные типы рассмотренных сред: m = 0 — однородная среда, соответствующая «опорному» слою; m = ± 1 — среды с локализацией изменения свойств в приповерхностной части слоя; m = ± 2 — среды с локализацией изменения свойств у основания слоя. Знаком « + » отмечено «нормальное» (материал слоя становится более жестким к основанию) изменение свойств слоя, знаком « - » — «аномальное» (материал слоя податливее у основания).

При проведении численного анализа будем различать:

– «акустически однородную» среду, в которой скорости объемных волн постоянны по толщине слоя, то есть изменение всех физических параметров материала (5) в направлении координаты x ₃ происходит по одному и тому же закону с равной интенсивностью:

f,(x3) = f.(x3) = fЛx3) = f(x3),     \p \u \л \f ;                       (25)

– «акустически неоднородную» среду, в которой скорости зависят от толщины:

f > ( x 3 ) * f ( x 3 ) , f . ( x 3 ) = f X x 3 ) = f ( x 3 ) , ^АР*^А f , ^АЦ = ^А^ = ^А f .                ⁽²6)

Здесь А 5 =

s _n) ¹ max ⁰⁷ X a e [ 0, h ]

| s ( x ₃ ) - s ₀| определяет

интенсивность изменения параметра s .

В [10] было введено понятие — «интегральный коэффициент неоднородности»:

1h f> ( x 3 )= J f ( x3 ) dx 3. h0

Как следует из рисунка 1, для пары сред типа m = 1 и m = - 2 этот коэффициент имеет одинаковое значение, равно как и для пары m = - 1 и m = 2 .

• 4.1.    Структура волнового поля в функционально-градиентном

«акустически однородном» слое

На рисунке 2 представлены кривые, иллюстрирующие поведение нулей (Рис. 2 а , б ) и полюсов (Рис. 2 в , г ) функции K ₂₂ (20)–(22) в зависимости от частоты при условиях (25). Здесь и далее цифры у кривых соответствуют функциональным зависимостям, представленным на рисунке 1. Пунктирные линии на рисунках 2 а и 2 б отвечают «опорному» слою ( m = 0).

Из рисунка 2 следует, что дисперсионные свойства слоев с m = 1 и 2, равно как и слоев с m = - 1 и - 2 совпадают, а поведение нулей функции K ₂₂ ( a , h , ю ) различно (Рис. 2 а , б ). Для слоев со свойствами m = - 1 и 2, а также для слоев с m = - 2 и 1 имеет место совпадение нулей, зато поведение полюсов в этих случаях различно (Рис. 2 в , г ). Особенности дисперсионных свойств «акустически однородного» слоя для рассматриваемых типов изменения параметров иллюстрирует рисунок 3, на котором приведены частотные зависимости относительных фазовых скоростей V F ( V F = ю/Е,, Е — решение дисперсионного уравнения задачи А ( а , ю ) = det R = 0).

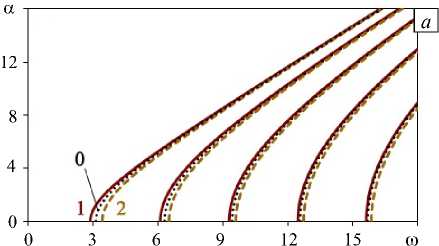
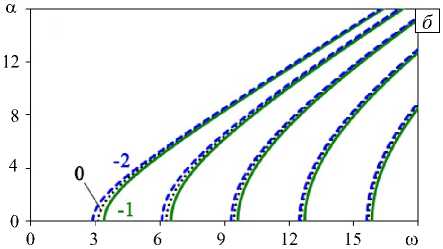
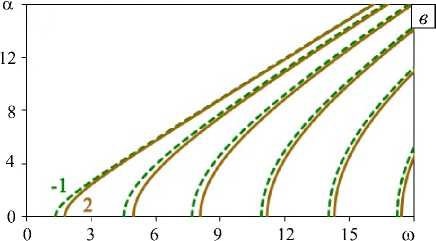
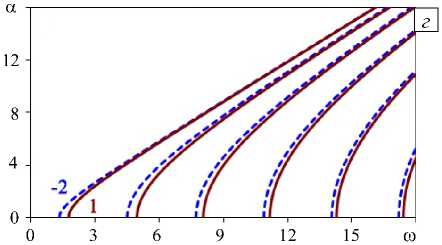
Рис. 2. Вид кривых нулей ( а , б ) и полюсов ( в , г ) функции K ₂₂ (α, h , ω) в зависимости от частоты для «акустически однородного» слоя при различном изменении свойств m : 0, 1, 2 ( а ); –2, –1, 0 ( б ); –1, 2 ( в ); –2, 1 ( г )

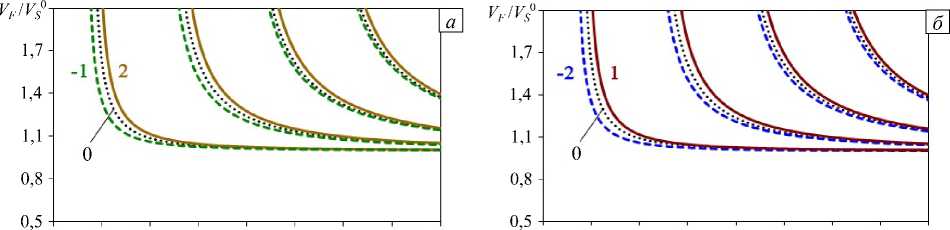
Рис. 3. Фазовые скорости в зависимости от характера неоднородности изменения физических свойств слоя, m : –1, 0, 2 ( а );

–2, 0, 1 ( б );

Представление о влиянии характера неоднородности на различные моды поверхностных волн дают относительные девиации их фазовых скоростей:

_F - V_F ^,   I/ V S ⁰ , δ = ( V F ⁰ - V F ^{m , ∆ρ}) / V_S ⁰ ,    ∆ ⁰ = V_F ⁰ - V_F^{m , ∆ρ}I/ V ⁰ ,

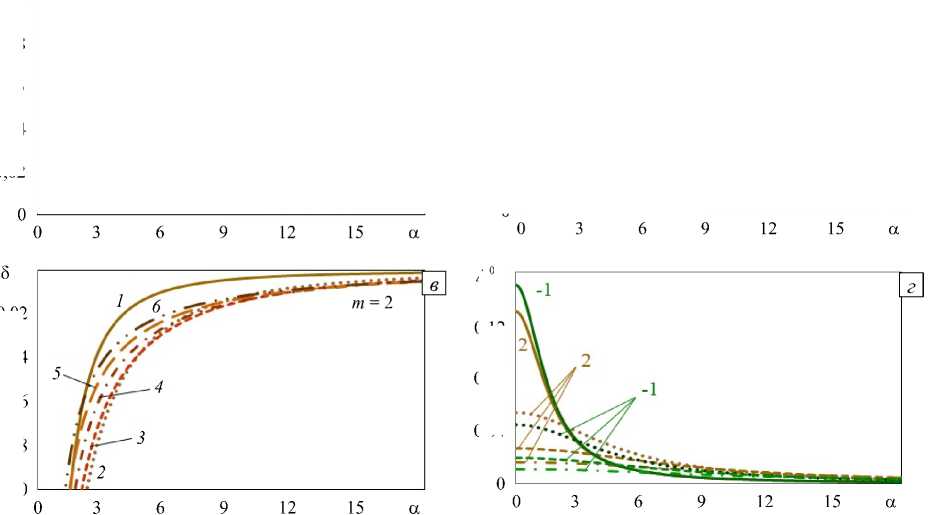
FF  S     FF  S     FF  F где VF0 — фазовая скорость однородного слоя из «опорного» материала ( m = 0 ), VFm, ∆ρ — фазовая скорость неоднородного слоя из функционально-градиентного материала, верхние индексы m =±1, ±2 отвечают закону изменения свойств, ∆ρ — интенсивности изменения плотности (в «акустически однородном» слое ∆ρ = ∆µ , «акустически неоднородном» слое ∆ρ ≠ ∆µ ). На рисунках 4а–в приведены зависимости относительных девиаций фазовых скоростей от волнового числа для первых 6-ти мод волн Лява в случае слоя с «аномальным» (Рис. 4а) и «нормальным» (Рис. 4б, в) характером изменения параметров. Для сравнения на рисунке 4г представлен параметр ∆0 (27) для первых 4-х мод поверхностных волн: сплошные линии соответствуют 1-м, пунктирные — 2-м, штриховые — 3-м и штрихпунктирные — 4-м модам. Как следует из рисунка 4, наиболее сильному влиянию характера неоднородности m подвержены 1-я и 2-я моды поверхностных волн, далее его воздействие ослабевает.

Наибольшее влияние «аномального» изменения параметров сказывается на 1 -й моде, в то время как на последующих модах сильнее отражается «нормальный» характер. В силу особенностей дисперсионных свойств слоя, по поведению фазовых скоростей невозможно судить о том, где локализована неоднородность в «акустически однородном» функционально-градиентном слое. Исходя из того, что область

0,02

A

0,08

0,06

0,04

A1

-0,02

-0,04

-0,06

-0,08

-0,10

Рис. 4. Относительные девиации фазовых скоростей для первых 6-ти мод поверхностных волн (кривые 1 – 6 ) в «акустически однородном» слое при различном изменении свойств: Д при m = - 1,2 ( а , б ); 6 при m = 2 ( в ); Д ⁰ при m = -1,2 ( г )

0,12

0,08

0,04

локализации изменения свойств слоя влияет на нули функции K ₂₂ ( a , h, ю ) , для анализа особенностей его динамики целесообразно исследовать амплитуду смещения поверхности слоя и ₂ ( 0, h, ю ) (23) и вклад в амплитуду смещений мод поверхностных волн и 2 ( 0, h , ю ) (24).

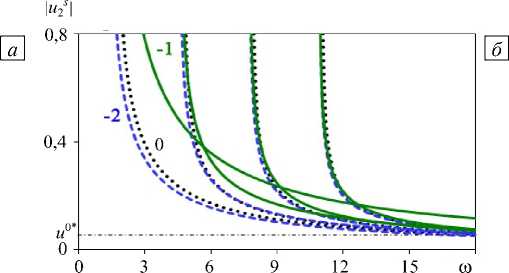
На рисунке 5 представлены зависимости амплитуд смещения первых 4-х мод поверхностных волн от частоты. Пунктирные линии на рисунках отвечают однородному, сплошные линии — неоднородному слою с локализацией изменения параметров в верхней (приповерхностной), штриховые — с локализацией в нижней (придонной) части слоя.

Рисунок 5 наглядно демонстрирует различие в поведении амплитуд смещений первых мод поверхностных волн при «нормальном» (Рис. 5 а ) и «аномальном» (Рис. 5 б ) характере изменения параметров «акустически однородного» слоя. Для амплитуд смещений поверхностных волн однородного слоя u ₂ ^s максимальное значение наблюдается в узком частотном диапазоне зарождения волны и далее 0*

падает до асимптотического значения u , причем выход на асимптотическое значение происходит последовательно. В неоднородном слое с «нормальным» характером изменения параметров, локализованным в верхней части слоя, падение значений амплитуд идет также последовательно, но более плавно относительно однородного случая: в рассматриваемом диапазоне амплитуды не имеют одного 0*      1*

минимального значения, выход на асимптотические значения ( и <  и ) совершается при значительно больших частотах. При локализации изменения свойств слоя в придонной области нарушается

0,4 -

1«2$1

0,8

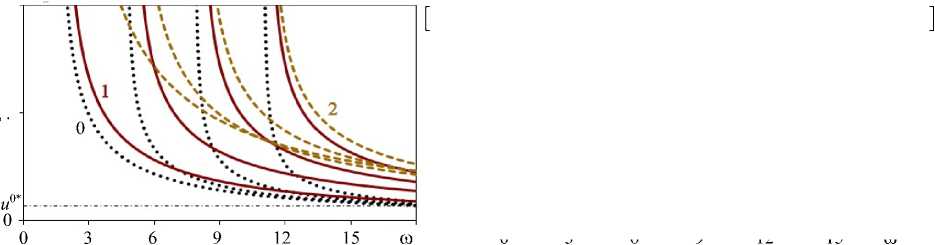
Рис. 5. Влияние характера и локализации неоднородности на амплитуды смещения первых 4-х мод поверхностных волн при «нормальном» ( а ) и «аномальном» ( б ) распределении свойств по толщине слоя; m = 1 и -1 - сплошные линии; m = 2 и –2 – штриховые; пунктирные линии – однородный слой

последовательность выхода на асимптотические значения: если для 2 -й и последующих мод минимальное асимптотическое значение равняется и ²* (причем u ²* >  и ⁰* ), то асимптотическое значение 1 -й моды превышает значение и ²* . Более наглядно этот эффект проявляется в неоднородном слое с «аномальным» характером изменения свойств, локализованным в верхней части (кривые для m = - 1, Рис. 5 б). При локализации неоднородности в придонной области слоя ее влияние незначительно, максимально - 2*      - 2*      0*

сказывается на 1 -и моде, минимальное асимптотическое значение составляет и ( и <  и ).

На рисунках 6 а - г приведены амплитудно-частотные характеристики «акустически однородного» функционально-градиентного слоя и * ( 0, h , ю ) (где и * ( 0, h , ю ) = и ₂ ( 0, h , ю )/ и ⁰ ( 0, h ,0 ) , и ⁰ ( x 1 , h , ю ) — смещение поверхности однородного слоя) с «нормальным» (Рис. 6 а , б) и «аномальным» (Рис. 6 в , г ) характером изменения свойств материала. На рисунках 6 а , в показаны амплитуды | и * ( 0, h , ю)| , на рисунках 6 б , г — фазы ф ₂ ( 0, h , ю ) смещения точки поверхности слоя.

|«2*                                                                 V2

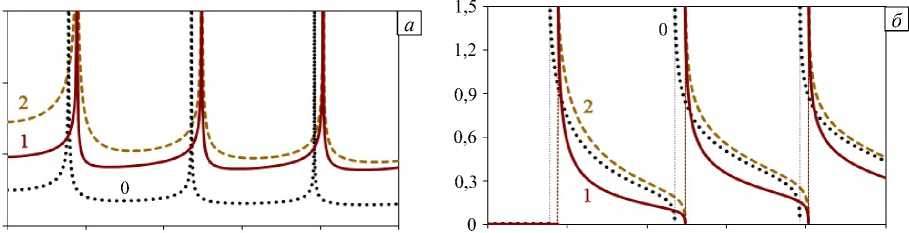
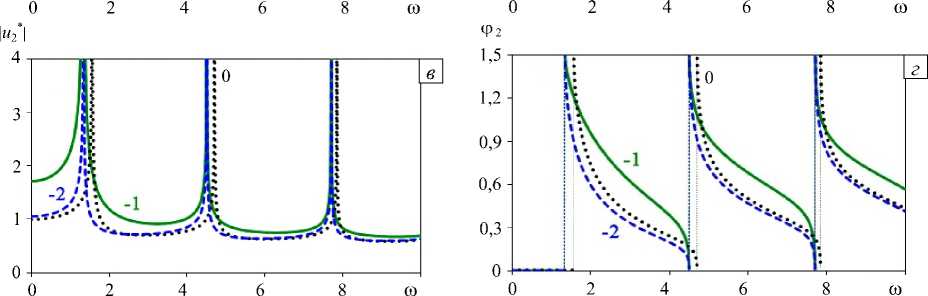
Рис. 6. Влияние характера и локализации неоднородности свойств в «акустически однородном» слое на амплитуды ( а , в ) и фазы ( б , г ) смещения поверхности: «нормальное» ( а , б ) и «аномальное» ( в , г ) распределение свойств; m = 1 и - 1 -сплошные линии; m = 2 и -2 - штриховые линии; однородный слой m =0 - пунктирные линии

Из сравнения частей рисунка 6 видно, что различное распределение свойств «акустически однородного» функционально-градиентного слоя сказывается на значениях резонансных частот: «нормальный» характер приводит к их увеличению, «аномальный» — к уменьшению. Положение области локализации изменения параметров влияет на величину амплитуды смещения вне резонансных областей.

• 4.2.    Влияние интенсивности изменения плотности на структуру

волнового поля в функционально-градиентном слое

На рисунке 7 показано влияние интенсивности изменения плотности на относительные фазовые скорости «акустически неоднородного» (26) слоя с «нормальным» (Рис. 7 а , б ) и «аномальным» (Рис. 7 в , г ) характером изменения физических параметров. Пунктирные линии отвечают случаю Ар ® 0, когда изменением плотности по толщине можно пренебречь, сплошные линии соответствуют меньшей относительно упругих модулей интенсивности изменения плотности: Ар = ( 1/2 ) Ац . Штрихпунктирными линиями отмечены асимптотические значения скоростей V®, J ^1/2 ( V 1⁰ = ^ ^Ар ” ⁰ , J -'¹² = ^ ^Ар = ⁽7^{2) А} н ).

Из сравнения рисунков 3 и 7 видно, что с уменьшением интенсивности изменения плотности слоя значения фазовых скоростей поверхностных волн падают, что связано с характером неоднородности свойств, областью локализации и особенностями условий на границах. При «нормальном» характере (Рис. 7 а , б ) влияние области локализации изменений обуславливается соотношением толщин низкоскоростной и высокоскоростной частей слоя. Роль защемления нижней грани незначительна, так как

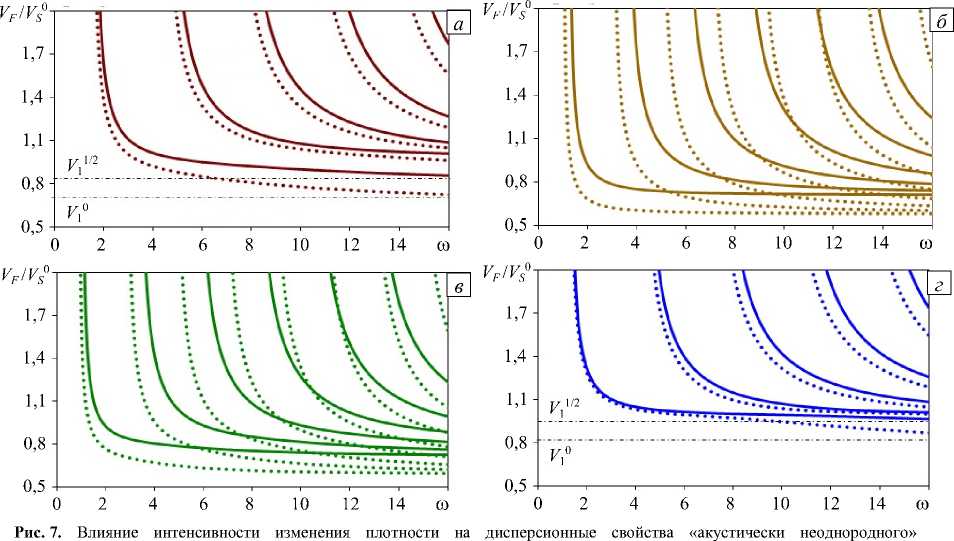
функционально-градиентного слоя при различном характере изменения параметров m : 1 (а); 2 (б); –1 (в); –2 (г); сплошные линии соответствуют ∆ρ = (1/2)∆µ , пунктирные – ∆ρ ≈ 0

в данном случае то, что материал становится более жестким, является естественным. При «аномальном» характере (Рис. 7 в , г ) влияние области локализации изменений по-прежнему зависит от соотношения толщин низко- и высокоскоростной частей слоя, роль защемления нижней грани становится более значительной, причем V ₁ ^∆ρ<  V ₁ ^∆ρ (Рис. 7 а , г ). В средах с зависимостями m = 2 и m = - 1 , то есть ¹ m = 1¹ m = - 2

низкоскоростная часть по толщине слоя становится преобладающей (Рис. 7 б , в ), в рассматриваемом частотном диапазоне существенно увеличивается число мод поверхностных волн.

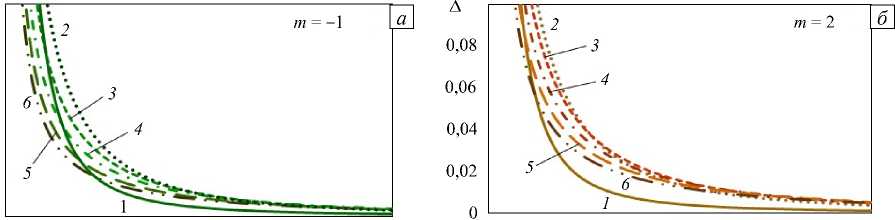
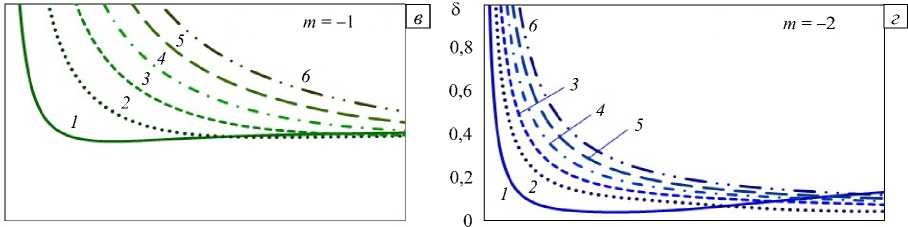
Рисунок 8 иллюстрирует особенности влияния характера и локализации неоднородности физических параметров по толщине слоя на различные моды поверхностных волн при слабо изменяющейся плотности ( ∆ρ ≈ 0 ). На рисунках 8 а – г приведены зависимости относительных девиаций фазовых скоростей для первых 6-ти мод (цифры на рисунках отвечают номеру моды) поверхностных волн от волнового числа в случаях «нормального» (Рис. 8 а , б ) и «аномального» (Рис. 8 в , г ) характера изменения упругих модулей. Рисунки 8 д , е содержит графики ∆ ⁰ (27) как функции волнового числа для первых 4-х мод (порядок мод отмечен типом линии см. Рис. 4 г ), цифры отвечают типу среды m (см. Рис. 1).

В отличие от «акустически однородного» слоя, уменьшение интенсивности изменения плотности приводит к качественным различиям в поведении девиаций фазовых скоростей (см. Рис. 4 в и Рис. 8 б ). Максимальные отличия от «опорного» случая ( m = 0 ) наблюдаются у девиаций в слое с m = 2 и - 1 (Рис. 8 д ). Изменения фазовых скоростей в слое из сред m = - 2 и 1 для 2 -х и последующих мод невелико, основное влияние в обоих случаях испытывают 1 -е моды (Рис. 8 е , значение ∆ ⁰ для 1 -х мод показано уменьшенным в 2 раза).

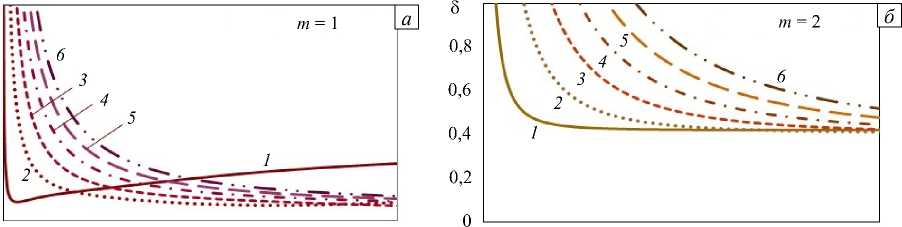
О 3       6       9      12      15 а          О 3       6       9      12      15 a

Рис. 8. Относительные девиации фазовых скоростей для первых 6-ти мод поверхностных волн в зависимости от волнового числа при «нормальном» ( а , б ) и «аномальном» ( в , г ) характере изменения свойств по толщине в случае ∆ρ ≈ 0 для первых 6-ти мод δ при m = 1 ( а ), 2 ( б ), –1( в ), –2 ( г ); для первых 4-х мод ∆ ⁰ при m = -1, 2 ( д ); и m = -2, 1 ( е )

О 3       6       9      12      15 а О 3       6       9      12      15 a

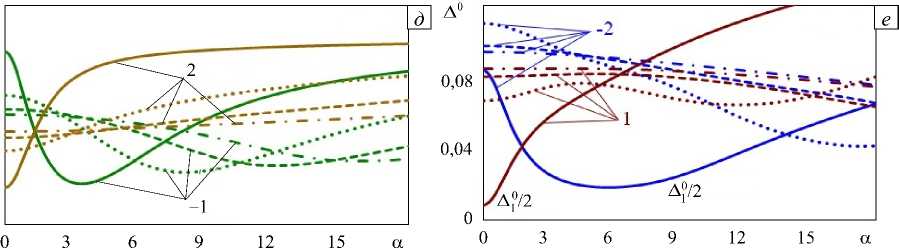
Рис. 8. Продолжение

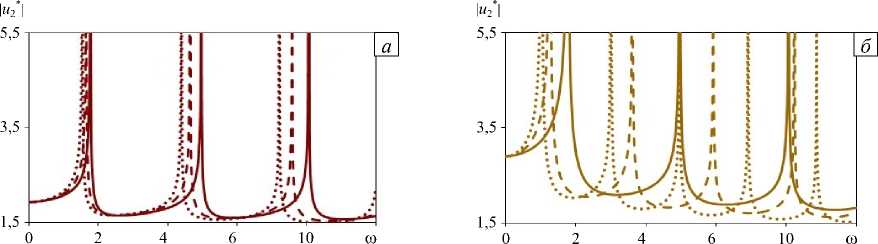
Далее на рисунках 9, 10 представлены графики амплитудно-частотных характеристик смещений u_г ( 0, h , го ) поверхности с «нормальной» (Рис. 9 а , б) и «аномальной» (Рис. 9 в, г ) неоднородностью свойств при слабо изменяющейся плотности ( Ар ® 0), а на рисунке 10 — при различной интенсивности изменения плотности материала слоя: Ар = Ац , Ар = ( 1/2 ) Ац и Ар® 0.

Из сравнения рисунков 6, 9 и 10 видно, что, в отличие от «акустически однородного» слоя, когда «нормальный» характер изменения параметров приводит к увеличению значения резонансных частот, а влияние области локализации никак не сказывается на этих значениях, в «акустически неоднородном» слое уменьшение Ар приводит к сдвигу резонансных частот влево при любом типе среды m , причем в случае m = 2 и m = - 1 происходит существенное увеличение числа резонансных частот (9).

"2*                                                                            <Р2

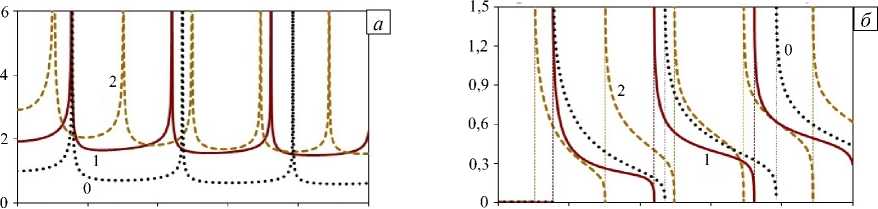
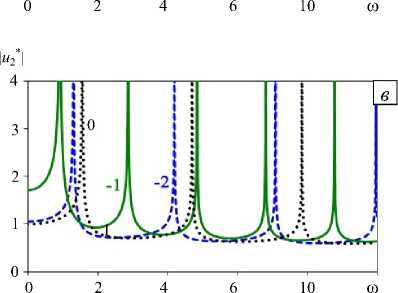
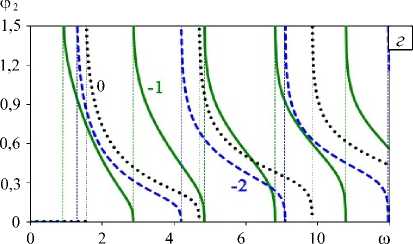
Рис. 9. Влияние характера и локализации неоднородности в слое на амплитуды ( а , в ) и фазы ( б , г ) смещения поверхности при Ар ® 0 и «нормальном» ( а , б ) и «аномальном» ( в , г ) изменении свойств; m = 1 и - 1 - сплошные линии; m = 2 и -2 -штриховые линии; m = 0 - пунктирные линии

"2*1

3,5

2.5

1.5

0.5

l"2*l

0         2        4         6         10 to                   0         2        4         6         10 со

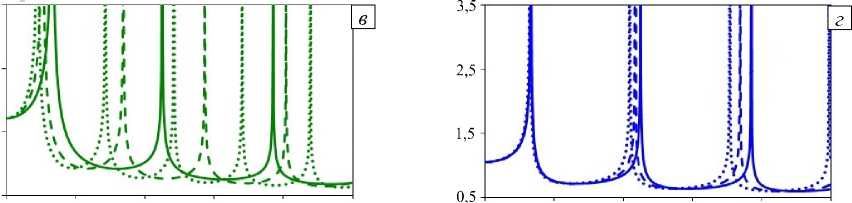
Рис. 10. Влияние интенсивности изменения плотности слоя Ар на амплитуды ( а , в ) и фазы ( б , г ) смещения поверхности слоя при различных типах неоднородности свойств: m = 1 ( а ); m = 2 ( б ); m = -1 ( в ); m = -2 ( г ); сплошные линии - Ар = Ац ; штриховые - Ар = ( 1/2 ) Ац ; пунктирные - Ар ~ 0

Влияние интенсивности изменения плотности на сдвиг резонансных частот растет с увеличением частоты (Рис. 10). Значение амплитуды вне резонансных областей падает с уменьшением Ар ; в средах типа m = 2 изменения максимальны, а в средах m = - 2 — минимальны.

5.    Заключение

В настоящей работе при построении функции Грина функционально-градиентного покрытия, совершающего гармонические колебания под действием поверхностного источника, использован предложенный в [11–15] подход. Применение специальной замены (7) при сведении системы обыкновенных дифференциальных уравнений 2-го рода с переменными коэффициентами к системе начально-краевых задач Коши позволило обойтись в матрице M ( а 1 , а ₂ , x 3 ) (8), (9) без производных функций, описывающих поведение свойств материала покрытия.

На примере сдвиговых гармонических колебаний функционально-градиентного слоя с монотонным изменением свойств исследовано влияние характера, интенсивности и локализации неоднородности материала на структуру и особенности распространения поверхностных волн. Рассмотрены «акустически однородные», в которых скорости объемных волн постоянны по толщине, и «акустически неоднородные» покрытия. Показано, что «акустически однородные» функционально-градиентные покрытия с различным характером и областью локализации неоднородности могут иметь равные дисперсионные свойства (см., например материалы с m = 1 и m = 2 (Рис. 1 а, б ), а также m = - 1 и m = - 2 (Рис. 2 в, г и Рис. 3 а , б )). Однако при одинаковых дисперсионных свойствах функционально-градиентные покрытия с разным характером и локализацией изменения свойств имеют существенно отличающиеся амплитудночастотные характеристики смещений отдельных поверхностных волн и 2 ( 0, h , ю ) и поверхности и ₂ ( 0, h , ю ) (Рис. 5, Рис. 6 а – г ).

Детально исследована роль интенсивности изменения плотности материала покрытия в формировании структуры поверхностного волнового поля. Установлено, что в отличие от «акустически однородного» слоя, в неоднородном покрытии влияние как характера, так и области локализации неоднородности на 1 -е моды поверхностных волн значительно больше и увеличивается с ростом частоты (Рис. 8 а – е ). Показана возможность управления резонансными эффектами — сдвигом резонансных частот, ростом или подавлением амплитуды смещения поверхности вне резонансных областей (Рис. 9, Рис. 10) за счет целенаправленного изменения свойств материала покрытия.

Работа выполнена при частичной финансовой поддержке РФФИ (проекты № 15-08-06074, 16-01-00647, 16-08-01052).