Особенности распространения волновых образований на основе гауссовских пучков

В работах [1–3] было предложено использовать суперпозицию гауссовских волновых пучков для теоретического описания физически реализуемого волнового процесса и изучения особенностей его распространения в пространстве, а также для формирования поля с помощью антенной решетки. Эта идея аналогична способу представления любого волнового поля, сосредоточенного в конечной области пространства, в виде суперпозиции плоских волн с тем или иным пространственным спектром. При этом волна в общем случае будет иметь искривленный фазовой фронт и неоднородное распределение амплитуды.

Преимущества формирования волнового поля в виде суперпозиции гауссовских пучков заключается в возможности управления параметрами пучка (шириной пучка, начальной кривизной волнового фронта) и угловым спектром, что позволяет достигнуть значительной локализации поля в пространстве. Если рассматривать задачу распространения радиоволн, то этот спектр можно отождествить со спектром излучаемого полезного сигнала.

В данной работе получено и рассмотрено решение приближенного параболического уравнения, описывающего волновое образование на основе суперпозиции гауссовских волновых пуков, имеющих поперечное распределение амплитуды и конечную кривизну волнового фронта. При

распространении такого волнового образования в пространстве происходит изменение амплитуды и искривление волнового фронта, возникает фазовая расстройка между отдельными составляющими поля. Эти особенности волнового процесса необходимо учитывать при описании распространения узких световых пучков, например, излучения оптических квантовых генераторов, а также при использовании гауссовских пучков в системах радиосвязи и беспроводной передачи энергии.

1. Решение параболического волнового уравнения на основе суперпозиции гауссовских пучков

Рассмотрим функцию вида

—°— exp I - ikz + i arctg I — w ( z )      I               I ^z 0

22 \ p       ik p I

-------— .

w ( z )     ² R ⁽ z )J

(

R ( z ) = z 1 + 0 , z ²

w ² ( z ) = w 2 1

2      2     2

p ² = X² + y 2,

z ² )

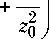
которая является решением параболического

волнового уравнения

2 ik ^ = 0 d z

и описывает простейший тип гауссовских монохроматических пучков [4; 5], w ₀ – начальная ширина пучка, константа z ₀ определяется из

граничных условий, w ( z ) – радиус светового пучка в поперечном направлении, а R ( z ) – радиус кривизны волнового фронта.

В работах [1; 3] было показано, что высокочастотные составляющие гауссовских пучков обладают малой дифракционной расходимостью. Также было предложено использовать суперпозицию гауссовских пучков (1)

да u (р, z, t)= J f (ф(р, z), t, k) A (k) dk,              (3)

-да где A(k) – частотный спектр излучаемого сигнала, для построения решения волнового урав-

да u (р, t, т) = J S (р, t, k) e-ikтdk,                     (7)

- да

где S ( р , t , k ) — пространственный спектр.

Подставляя (7) в (6), получаем уравнение для пространственного спектра S ( р , t , k )

д ² S 1 д S 2 ik д S _п

+      -        = 0.

др ²    р др c д t

Решением уравнения (8) является (см. [7])

да ik         [ ik            ]

S (р, t, k )=     § exp I--(р2 +^2 )lx ct         V ct           7

функция

нения

A u =

1 д ² u c ² д t ² .

^x I 0

ik

I — р^ l S 0 fc k ) d ^ ,

V ct 7

В работе [3] было показано, что суперпозиция гауссовских пучков вида (3) обладает большей локализацией в пространстве по сравнению с одиночным пучком, если спектр A ( k ) сдвинут в высокочастотную область.

Рассмотрим, особенности распространения в пространстве волнового образования (3) с гауссовским поперечным профилем (немонохроматический пучок). Для этого нам необходимо искать решение волнового уравнения (4) в виде (3) с учетом соответствующих начальных условий.

Введем новую переменную т = z - ct , т. к. решение рассматривается в системе координат, движущейся со скоростью c вдоль оси z . Из (4) с учетом осевой симметрии пучка получаем сле-

где I ₀ ( x ) – модифицированная функция Бесселя первого рода, S _o( ^ , k ) — пространственный спектр в начальный момент времени t = t 0 . Подставляя (9) в (7) и учитывая, что 1 0 ( ix ) = J 0 ( x ) [7], где J ₀( x ) – функция Бесселя, получаем решение параболического волнового уравнения (6)

u ( р , t , т ) =

i да да              г ik z                  а

= — fd ^ dk ^ k exp |--(р2 +^)- ik т | x ct                   V ct                 7

0 -да

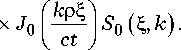
дующее уравнение в новых переменных

Можно считать, что начальный спектр S 0 ( ^ , k ) описывает распределение поля в начальный момент времени в плоскости антенной решетки и содержит частотные составляющие излучаемого

д2и   1 ди  2 д2 и    1 д2u др2   р др   c дtдт   c2 дt2

сигнала.

Так как решение волнового уравнения ищет-

Для исследования особенностей распространения суперпозиции гауссовских пучков, будем искать решение приближенного параболического уравнения, получаемого из точного волнового уравнения (5). Это приближение получается при условии медленного изменения огибающей волнового образования (3) при его распространении (см. [6]). В этом случае можно пренебречь

1 д2 u второй производной       . Тогда уравнение c 2 д tt

ся в виде суперпозиции гауссовских пучков, то возьмем начальный спектр в соответствии с (1) в виде

S0 (^, k) = A (k) exp (-71w2) exp (ik7/2R), (11) где A(k) – спектр излучаемого сигнала s(t). Подставляя (11) в (10) и учитывая, что [см. 8; 9] да10 (2VOt) e-ptdt = - eap, Re (p) > 0, 0                   p получаем

примет вид д2u 1 дu 2 д2 u „

—- +--+--= 0.

др ² р др c д t дт

i ( ^{u ( р} '*' ^{т )} = 2 ct ^exp

2 2 A р r

2 2/2 w c t

x

да да

Запишем решение уравнения (6) в виде разложения по плоским волнам

x J dk J d £ ,kA ( k ) exp

-да

- 1^ 22.

2 ct

V

-

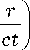
A - ik т

x (12)

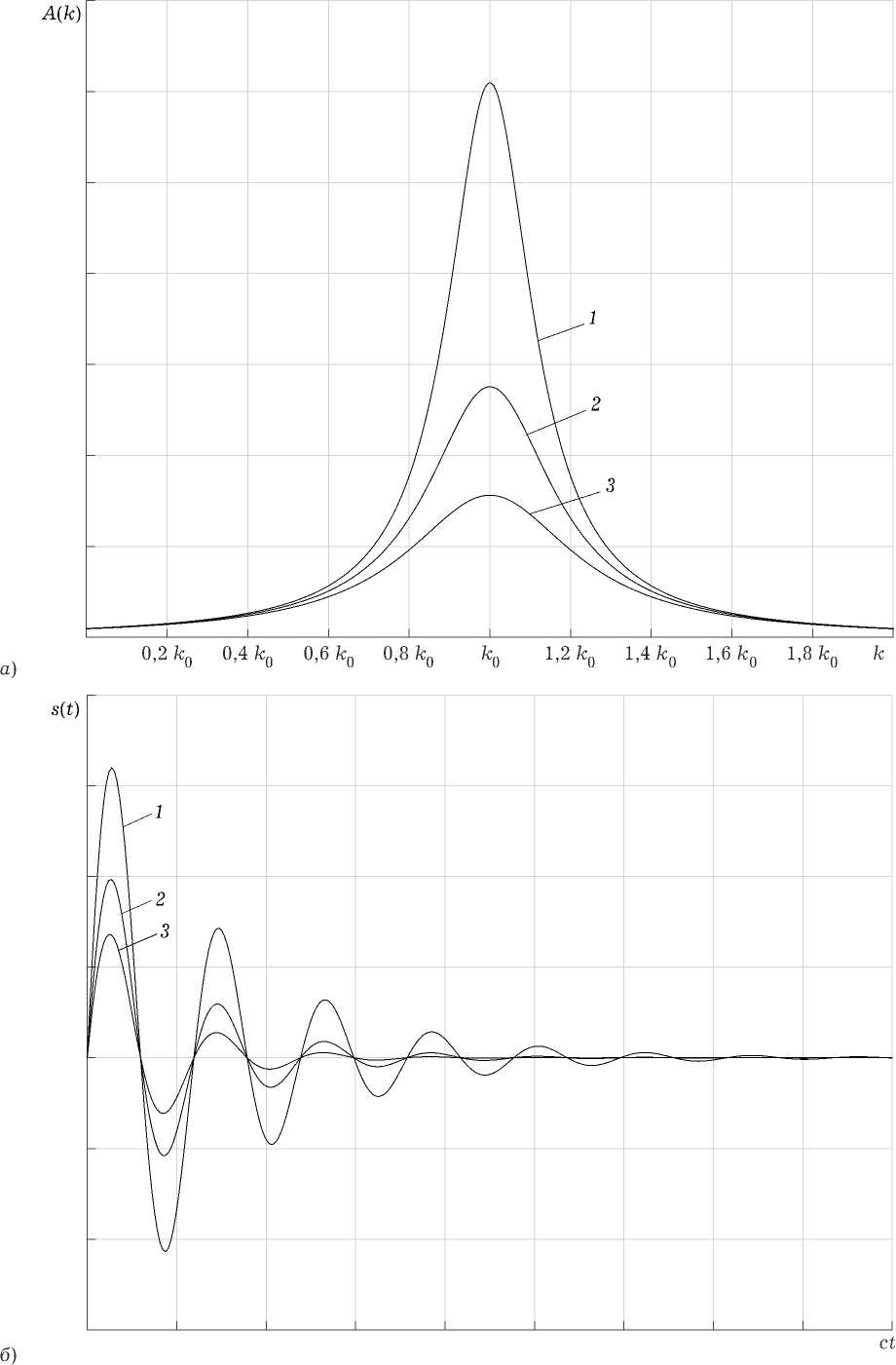
Рис. 1. Вид частотного спектра A ( k ) ( а ) и сигнала s ( t ) ( б ) для значений параметров a = 0,1 k ₀ (кривая 1), a = 0,15 k ₀ (кривая 2), a = 0,2 k ₀ (кривая 3)

^X I 0

где 1 r = 1/ ct - 1/ R .

В качестве спектра A ( k ) для простоты возьмем функцию вида

R2     + a w2 (ct — R )2 + 2 (ct — R)

i n /2

где k = to/ c , a e i ^{п /2} - множитель, определяющий начальную фазу. Спектр (13) соответствует сигналу s ( t ), определяемому преобразованием Фурье [6]:

R ²

w ⁴ ( ct — R ) ²

1 a w2  2r

1         ■ 2,2

a I kkiL w ² 2 r ^J 4 r ² J

Используя параметры R , a , k ₀ можно управ-

лять расходимостью волнового фронта пучка

s ( t ) = e i ^{n /2} f ------ A 2------ e- i ^to t d to =

, (to — to0 ) + a2

и его локализацией в пространстве. При этом имеют место конкурирующие эффекты фокусировки волнового поля и дифракционной рас-

= ^^ O c exp ( — act — i _Ю о t + i n /2 ) .

Вид спектра A ( k ) и сигнала s ( t ) показан на рис. 1, а , б .

Производя интегрирование в (12) с учетом (13) и подставляя 1/ r = 1/ ct — 1/ R , окончательно получаем решение приближенного волнового уравнения (6) с начальными условиями, определенными в (11) и (13).

ходимости, известными для монохроматических пучков [5]. В соответствии с формулой (16) при k o » 1 минимум W ( ct ) достигается при ct « R (точка фокуса). Из (16) получаем, что начальная ширина пучка равна

W ( ct)

1a w2 — 2R

и чтобы она имела физический смысл, необхо-

и ( р , t , т )

x exp

e ^{n /2} i л/2 act

1 ik + a 1

+ ⁰

w2      2   (ct p2 R 2

w

.⁴ ( ct — R ) ² J_

w

ik o + a ( 1

2 I ct

^^^^^^в

R

x

димо

2 R

— >  a . w ²

Так как из (13) следует, что ширина A k спектра F ( k ) пропорциональна параметру a , то (18)

можно переписать как

X exp

—

p ² R ²

( x exp

w ² ( ct — R )' ^ik o P² _—,

2( ct — R )

exp

/ ik o T .

(        2

—

2( ct — R)

2 R

— > A k . w ²

2. Особенности распространения немонохроматического пучка в пространстве

Рассмотрим основные особенности распространения волнового образования (15). При сравнении (15) с начальным распределением поля в (11), можно увидеть, что с расстоянием вдоль оси z изменяется множитель, определяющий амплитуду в направлении, перпендикулярном оси пучка (он также зависит от параметров частотного спектра a и k ₀).

Дифракционная расходимость в (16) определяется зависимостью ширины пучка от расстояния:

Это означает, что для излучения широкополосного спектра необходимо использовать пучки с большим радиусом начальной кривизны.

Зависимости ширины пучка W ( ct ) для разных значений параметров R , a , k ₀ представлены на рис. 2, а , б . Видно, что при k o » 1 имеются хорошо выраженные минимумы. Таким образом, высокочастотные составляющие легче сфокусировать, однако при дальнейшем распространении немонохроматический пучок будет и достаточно быстро расходиться. При увеличении ширины спектра A ( k ) (параметра a ) увеличивается число высокочастотных составляющих, обладающих меньшей дифракционной расходимостью,

и расходимость немонохроматического пучка в целом становиться более медленной. При отсутствии фокусировки ( R ^ да ) наблюдается наиболее медленная расходимость, однако такой пучок нереализуем на практике, так как он яв-

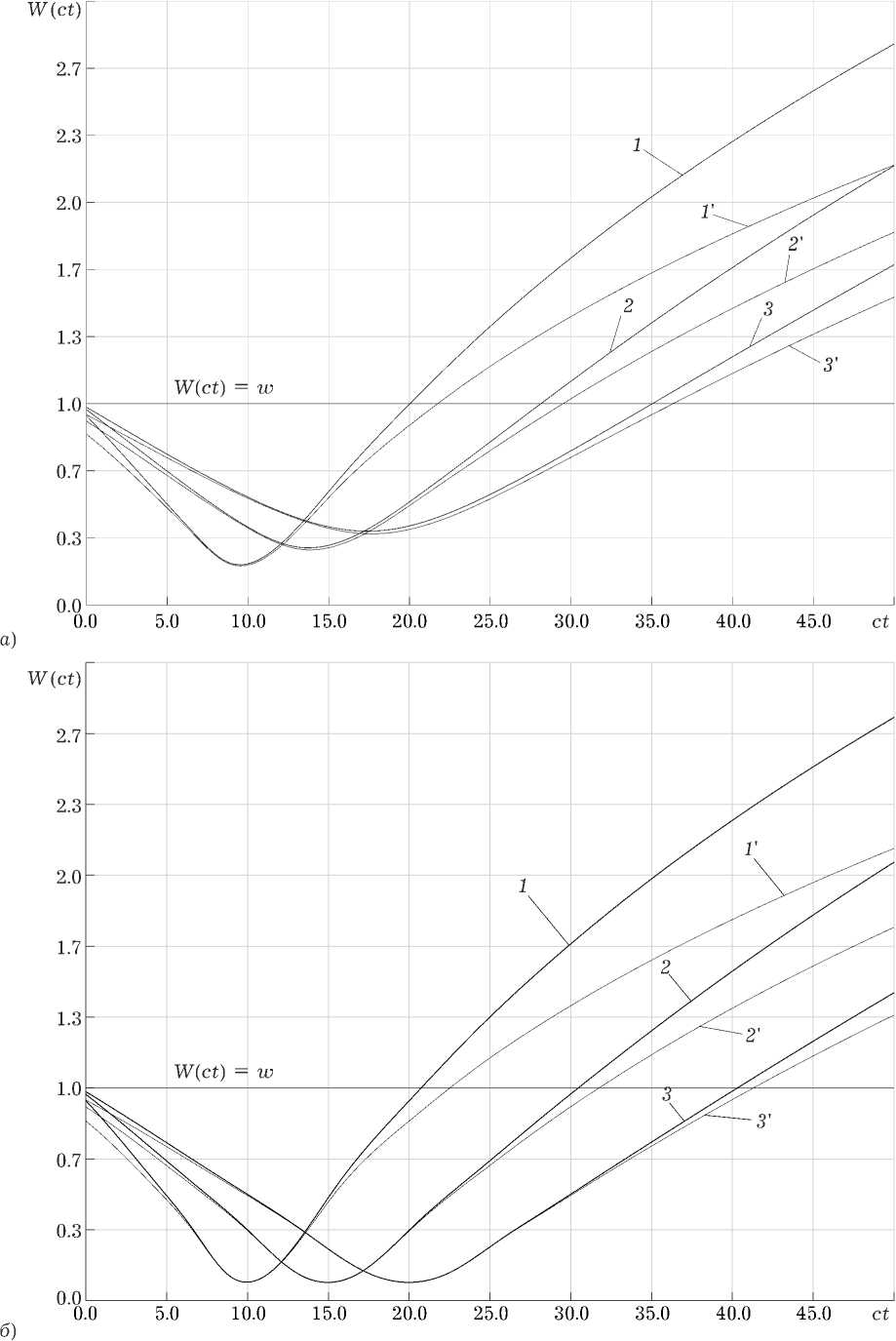
Рис. 2. Зависимость ширины пучка W ( ct ) при разных значениях кривизны волнового фронта R = 10 (кривая 1-1’), R = 15 (кривая 2-2’), R = 20 (кривая 3-3’), ширины спектра a = 30 (сплошная кривая), a = 10 (штриховая кривая), и k ₀: а ) k ₀ = 100; б ) k ₀ = 1000

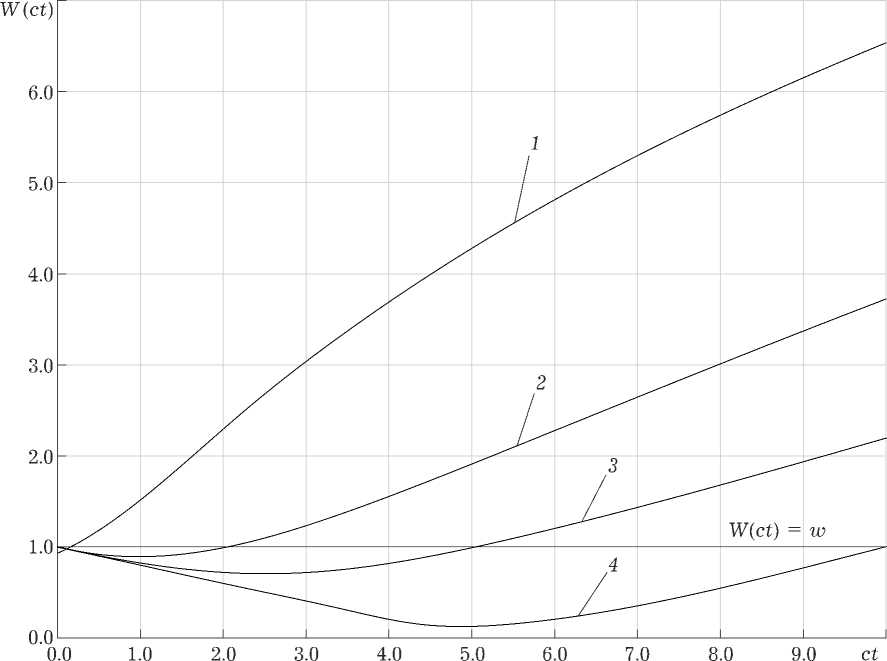
Рис. 3. Зависимость ширины пучка W ( ct ) при разных значениях к₀ = 1 (кривая 1), к д = 5 (кривая 2), к д = 10 (кривая 3), к д = 100 (кривая 4) и кривизне волнового фронта R = 5

ляется квазиплоской волной, для формирования которой потребуется антенна с апертурой бесконечно большого размера.

Таким образом, подтверждается явление малой дифракционной расходимости высокочастотных составляющих волнового поля и целесообразность применение сфокусированных немонохроматических пучков с конечной кривизной волнового фронта.

При этом необходимо соответствующим образом подбирать параметры R , a , k ₀ для достижения требуемого распределения поля в про-

В формуле (15) также можно выделить функцию, описывающую фазовый сдвиг суперпози-

ции волновых пучков

ф ( ct , p ) =

k ₀     p² R __1________

² ct w ⁴ ( ct - R ) f 1 a )²   k 2 ²

I w ²   2 r J     4 r r

^k 0 p ²

2( ct - R )

arctg

( ъ \ ^k0

2 r + a

странстве.

На рис. 3 представлена зависимость W ( ct ) при фиксированном радиусе кривизны R и разных значениях k ₀; при больших k ₀ явление фокуси-

ровки поля проявляется достаточно хорошо, и минимумы более ярко выражены.

На достаточно большом расстоянии вдоль оси z , т. е. при ct ^ м , волна (16) переходит в

i п / a    e ^{п /2}

2 ct   1 _ ik0 + a w2    2R

e - ^{a т}

_e ^{_ ik} 0 ^T

т. е. становится эквивалентной излучаемой плоской волне (15), распространяющейся с затуханием 1 ct .

В (22) второй (линейный по k ) член определяет непосредственно задержку между отдельными составляющими на некоторой эквивалентной частоте k ₀ в соответствии с (1). Остальные члены являются поправками, которое фактически определяют изменение фазового фронта и формы пучка при его распространении.

На рис. 4 представлена зависимость функции ф от расстояния вдоль оси z . Как видно из графиков, в окрестности точки ct « R , где ширина пучка достигает минимума, происходит скачок фазы, который тем больше, чем больше расстояние от оси пучка, то есть составляющие волнового поля запаздывают тем сильнее, чем дальше они находятся от оси z . Это может негативно сказаться на приеме и обработке полез-

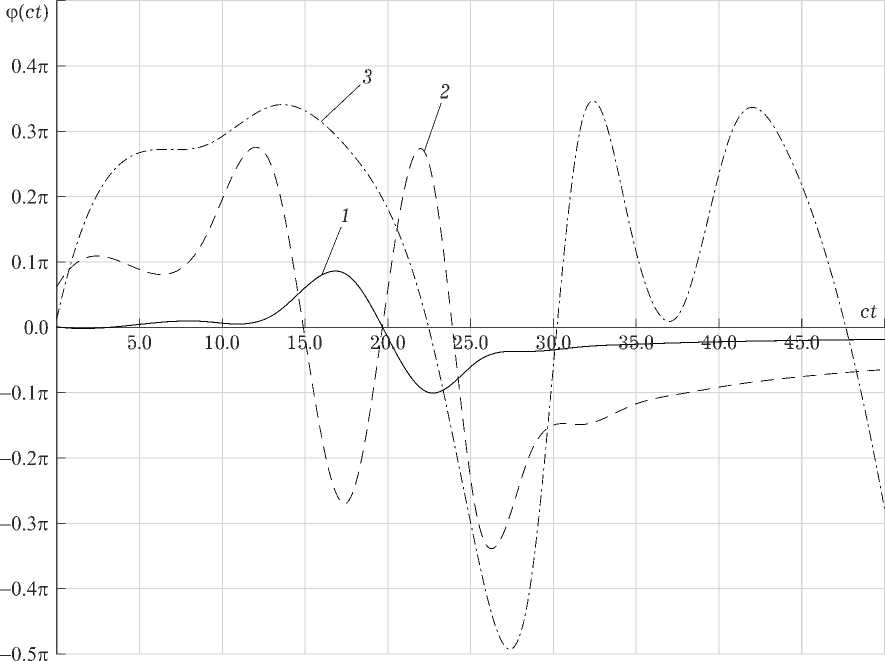
Рис. 4. Зависимость фазового сдвига Дф ( ct ) при разных значениях расстояния р = 0,01 (кривая 1), р = 0,05 (кривая 2), р = 0,3 (кривая 3) от оси пучка и параметрах к о = 1000, R = 20, a = 30

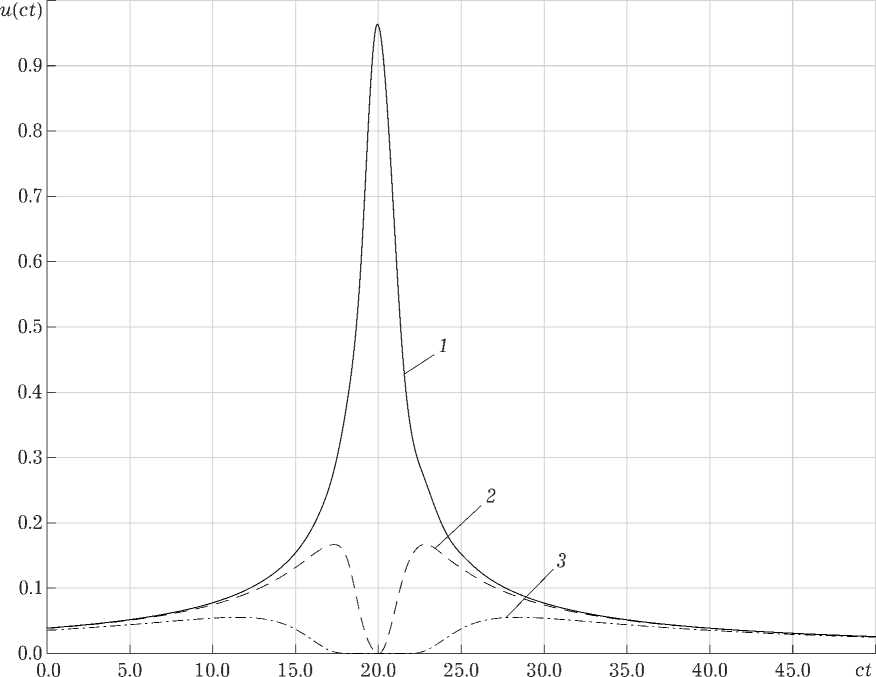
Рис. 5. Временные диаграммы импульса для разных расстояний от оси пучка р = 0,01 (кривая 1), р = 0,05 (кривая 2), р = 0,3 (кривая 3) и параметрах к о = 1000, R = 20, a = 30

ного сигнала. Однако величина поля достаточно быстро спадает при удалении от оси пучка, и в точке ct ≈ R можно пренебречь составляющими с малой амплитудой волны, так как они будут давать незначительный вклад в суммарное волновое поле.

На рис. 5 изображены временные диаграммы импульса u ( ρ , t , τ ) для значения τ= 0, то есть системе координат, движущейся со скоростью c вдоль оси z , и для разных расстояний от оси пучка. На них также видно отличие запаздывания для составляющих, находящихся на разных расстояниях относительно оси пучка.

Заключение

В работе получено и рассмотрено частное решение параболического волнового уравнения, описывающего распространяющееся в пространстве поле в виде суперпозиции гауссовских волновых пучков (немонохроматический пучок). Такое волновое образование имеет конечный спектр, а потому физически реализуемо и может применяться для описания распространения сверхширокополосных импульсов, а также для их формирования с помощью антенных решеток.

Было показано, что с помощью подбора значений параметров пучка и спектра сигнала можно получить значительную локализацию поля в пространстве за счет фокусировки волнового фронта, что приводит к уменьшению ширины пучка. Использование широкополосного спектра позволяет добиться меньшей дифракционной расходимости. Эти обстоятельства могут быть полезны при использовании сигналов на основе гауссовских пучков для радиосвязи. Практически этот сигнал может быть получен с помощью антенной решетки, элементы которой должны

возбуждаться независимо друг от друга. Также возможно усовершенствовать дифракционные свойства импульса с помощью неоднородного распределения элементов решетки [2].

Достоинства гауссовских пучков позволяют использовать их в системах связи, дистанционных измерительных приборах, радиолокации и беспроводной направленной передаче энергии на расстоянии.