Особенности решения обратной задачи кинематики для ротопода

На кафедре «Автоматизация механосборочного производства» Южно-Уральского государственного университета ведутся разработки устройства формирования дополнительных технологических координат на основе механизма с параллельными кинематическими цепями, которое может быть альтернативой двухкоординатным поворотным столам.

На рис. 1 показана трехмерная модель такого устройства, которое состоит из подвижной платформы, основания, модуля привода, кольцевой направляющей, шести штанг и шести кареток, имеющих возможность движения по кольцевой направляющей. Выходным звеном механизма, лежащего в основе устройства, является подвижная платформа.

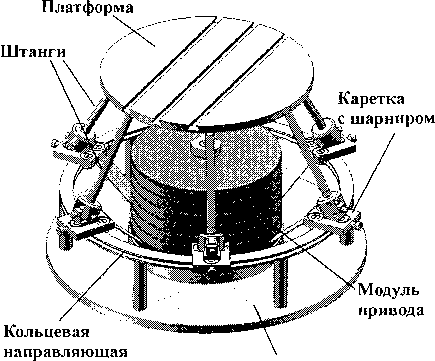
Основание

Рис. 1

При кинематическом анализе данного устройства, а также при построении алгоритмов управления движением подвижной платформы возникла потребность в решении обратной задачи кинематики о положениях, которая формулируется как определение входных (управляемых) координат устройства по известным выходным.

На рис. 2 представлена упрощенная кинематическая схема механизма, состоящая из подвижной платформы (с полюсом С ), соединён- ной с неподвижным основанием с помощью шести штанг постоянной длины. В литературе [1] такой механизм принято называть ротоподом. Сферические шарниры В,-(/ = 1...б) связывают штанги с подвижной платформой, координаты этих шарниров в связанной с платформой системе координат (СК) CX’Y’Z’ будем определять через углы фв :

^х\ = Кпл ^СО5Фв,, ^'b, = ^кпл sinФв, ’ Z = 1... 6 .

Расчет и конструирование

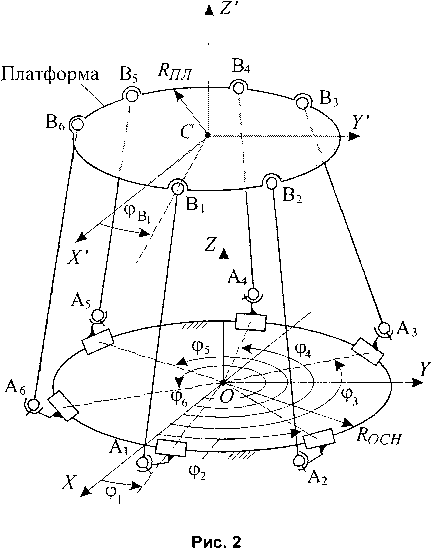
Угловые положения кардановых шарниров A_z (z = 1...6), расположенных на каретках, могут изменяться за счёт перемещения кареток по круговой направляющей. При этом будут изменяться угловые координаты кареток cp_z (z = 1...б). Примем эти величины за входные (управляемые) координаты. Будем считать для простоты, что координаты кардановых шарниров в неподвижной СК OXYZ определяются этими же координатами следующим образом:

^хк,^=косн^С№^ У\,^=косн™^, i = l.-.6. (2)

Координаты z_A кардановых шарниров должны быть заданы; координаты z’_B сферических шарниров примем равными нулю.

Конструкция механизма обеспечивает движение инструмента (детали), закрепленного на подвижной платформе ротопода, по шести независимым координатам: трём линейным Хс, Yc, Zc и трём угловым у, 9, у (на рис. 2 не пока заны). В качестве линейных выступают координаты полюса С платформы в неподвижной СК OXYZ . Угловые координаты определяют разворот подвижной платформы вокруг полюса; в качестве этих координат могут использоваться, например, углы Крылова, определяющие разворот связанной с платформой СК CX'Y'Z' относительно неподвижной СК OXYZ. Шесть описанных координат будут являться для рассматриваемого устройства выходными координатами.

Для получения уравнения математической модели ротопода, связывающей угловые коорди наты шарниров, расположенных на каретках, с выходными координатами воспользуемся уравне ниями:

^£2=(*А, "^^(Уа, “Ув^^А, ~^ZB,)², Z=1...6>                           (3)

которые с учётом уравнений (2) примут следующий вид:

$ ={^ROCH ^СО8Ф₍-^^^(^сн sine?, - №j²+(^zA, ~^zbJ²> A =£ = const, t = 1...6,     (4)

где координаты х_в , у_в , z_B. сферических шарниров должны быть определены в неподвижной СК OXYZ . Пересчет координат сферических шарниров из связанной с платформой СК CX'Y'Z’, в которой они заданы, в неподвижную СК OXYZ осуществляется с использованием следующего

матричного преобразования: Гх ^ ХВ; (к h Ч ^cV^ УВ, тх т2 т3 Ус у'В/ 2В, «1   «2   «3 zc ^'В, < 1 ) (о 0 0   1 J / в котором направляющие косинусы lk.mk,nk ^к-\..3^ определяются через выходные угловые координаты следующим образом (в качестве выходных угловых координат использованы углы Крылова):

l_x = cos уcosу + sin9sinysiny; Z₂ = sinycos9; Z₃ =-cos у sin у + sin 14/ sin 9 cos у ;

m_x = -sinycosy + sin 9 cos ф sin у ; m₂ = cos 4/ cos 9; m₃ = sinysiny + cosy sin 9 cos у;       (5)

n_x = cos9siny ; n₂ = -sin9 ; n₃ = cos9cosy .

Петрова Л.Н.

Раскрывая в (4) скобки и вводя следующие обозначения:

а/ = -ISoch^ , р, = -2Rqch ув.,.

у; =Z2-/(^-zA.+2zA;zB/-хв.-у^.-zBf, z = 1...6, запишем (4) в упрощенном виде:

а,со8фу+Р,зтф,-у, =0, z = 1...6.               .(?)

Каждое из уравнений (7) можно представить в форме квадратного относительно sincpz:

^ яш2ф, + л, зшф, + X,- = 0,(8)

где ^ = а2 +р2, л, = -2у,Р,, \ = у2 -а2, z = 1...6.

Решение уравнений (7) позволит определить угловые координаты ф( (z = 1...6) кареток (кар дановых шарниров), соответствующие заданным выходным координатам Хс, Yc, Zc, ху, ^, 'У, т. е. решить обратную задачу кинематики о положениях. Так как угловые координаты представляются действительными числами, то при решении уравнений необходимо контролировать выполнение следующих условий:                          -

^-44Л>0;

|8Шф,|<1.     '

Выражения для определения угловых координат кареток имеют следующий вид:

Ф,

= arcsin

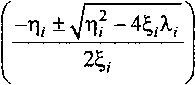
/ = 1...б.

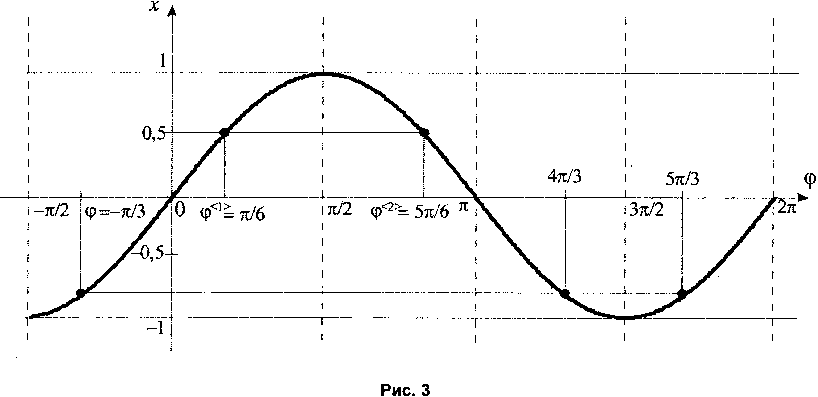
При вычислении углов ф^ используется круговая функция ф = arcsin х [2], главные значения которой лежат в диапазоне Е-/^» ^] • Однако реальные углы ф( должны принимать значения в диапазоне [0,2л] (см. рис. 2). Рис. 3 иллюстрирует случай, когда двум углам о = — и

Ф<2> =— соответствует одно значение функции зшф = 0,5 . Следовательно, при расчете углов б

Ф₍ с использованием (9) без учета этой особенности функции ф = arcsin х часть решений может быть потеряна.

Чтобы избежать потери решений, введем следующие условия:

• -    если определенная с использованием (9) угловая координата лежит в диапазоне 0 < ф < ^, то введем дополнительное значение ф* = л - ф;

  
  
  

Расчет и конструирование

• -    если определенная с использованием (9) угловая координата лежит в диапазоне -^ < ф < О (см. случай ф = -^ на рис. 3), то введем два дополнительных значения ф’ = я - ф, ф" = 2л + ф.

Наличие знака «±» в выражениях (9) приводит к двузначности решения уравнений (7). Каждому найденному с использованием (9) значению угловой координаты будут соответствовать два значения, лежащие в диапазоне [0, 2л]. В результате для каждой угловой координаты будет получено 4 значения, удовлетворяющего соответствующему уравнению (7).

Решение прямой задачи кинематики применительно к ротоподу, имеющему следующие геометрические параметры: ф_в=[10 50 130 170 250 290], 7?_ося = 200 мм, К_пл =100 мм, L = 143,5 53 8 мм, при выходных координатах х_с=0, у_с=0, z_c= 100 мм, ф = 0, 3 = 0, у = 0 привело к следующим результатам:

Ф^О 20 160 180], ф2 =[40 60 120 140], фд =[40 60 120 140],

Ф4=[0 20 160 180], ф5 =[240 260 280 300], фб =[240 260 280 300].

Для каждой из входных координат ф; получено четыре значения. Следовательно, необходимо ввести некоторые условия, которые позволят осуществить выбор одного угла из четырех.

Одним из условий может быть контроль расстояния от шарнира Bz до возможных положений шарнира Az, определяемых четырьмя значениями угла ф7:

^> = дУс^ося^^8^?^^                                           > £ = 1... 4 .

Значения углов, для которых I^^k> ^ L , должны быть отброшены.

После того как будут проконтролированы расстояния Ц^к>. для каждого шарнира каретки останется только два возможных значения его угловой координаты (рис. 4). На рис. 4, а показаны все возможные положения шарниров каретки, на рис. 4, б - только те, для которых выполняются условия Ц^к> = L.

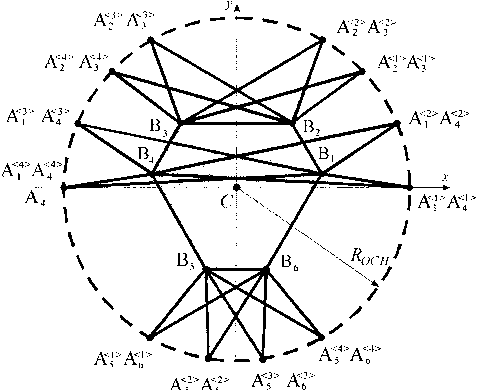
Рис. 4

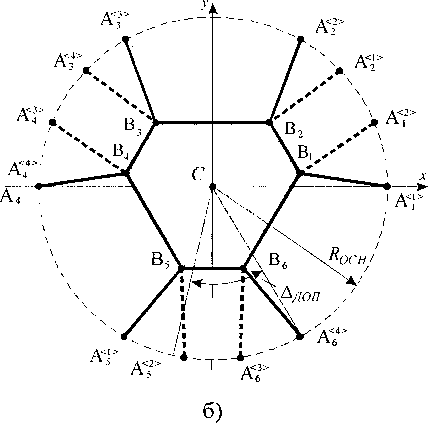
При выборе одного из двух возможных положений шарнира каретки следует учитывать условие отсутствия соприкосновения кареток, которое сводится к проверке неравенств

|ф/ -Ф/+1| -^доп ’ где угол ^дoп задается из конструктивных соображений. На рис. 4, б отвечающие данному условию положения штанг, обозначены сплошными линиями.

Дополнительное условие, которое будет влиять на выбор единственной угловой координаты для шарнира каретки, может быть сформулировано из анализа жесткости устройства в требуемом направлении (см. статью В.А. Смирнова и Е.Ю. Сулацкой в данном Вестнике).

Все рассмотренные выше условия должны быть учтены при разработке алгоритмов управления ротоподом.