Особенности течения неньютоновских сред в осциллирующих реометрических системах

При планировании корректных экспериментов по идентификации реологической принадлежности жидкостей и определения их параметров необходимо учитывать особенности течения сред различных реологических типов. Рассмотрим подробнее два типичных нестационарных случая: затухающие колебания крутильно-колебательного вискозиметра (рис. 1) и вынужденные колебания вибрационного вискозиметра (рис. 2) (см., например, [1]).

В подобных периодических течениях на практике обычно реализуются случаи, когда полная деформация остается сколь угодно малой, хотя ее мгновенная скорость может быть высокой. В этом случае состояние простой жидкости с затухающей памятью можно охарактеризовать как линейное вязкоупругое, а течение описать единственной материальной функцией - комплексной вязкостью. В этом случае для установившегося режима вискозиметрические уравнения могут быть получены аналитически, и в детальном изучении локальных особенностей течений таких сред нет необходимости. Поэтому далее остановимся на рассмотрении течений неньютоновских жидкостей, в реологические уравнения состояния которых входят нелинейно вязкие или вязкопластические составляющие.

Математическая формулировка задачи

Крутильно-колебательный метод

Математическую модель эксперимента для случая длинного цилиндра в цилиндрической системе координат представим в следующем виде:

• 1)    уравнение движения жидкости

dU j^ + 2^                (П

d T   д^     ^                                    ’

• 2)    уравнение движения цилиндра

  

  2 H

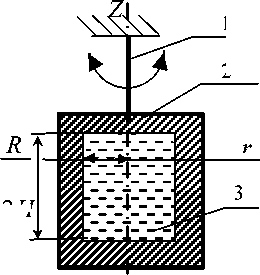
  Рис. 1. Схема метода:

  1 – упругая нить; 2 – цилиндр, совершающий затухающие крутильные колебания вокруг своей оси; 3 – исследуемая жидкость

  
  
  

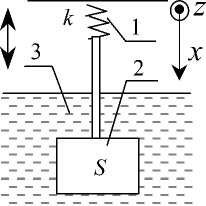
  Рис. 2.Схема метода:

  1 – упругий элемент; 2 – пластина, совершающая плоские колебания под действием гармонич. силы;

  3 – исследуемая жидкость

  
  

  _d 2 _α dT ²

  
  

  d α

  + 2 ∆    + α = P ,

  ⁰ dT ^,

  
  
  
  

• 3)    начально-краевые условия для (1), (2):

  где

  
  

  U ( ^ ,0) = 0, U( ^ ₀ ,T ) = d ".    и (0, T ) = 0, a (0) = a   6 - , d a

  dT                           dT

  
  

  • 4)    реологическое уравнение состояния

    • 4.1)    для ньютоновской среды

  ^σξϕ ^{= D} ξϕ ^,

  
  

  = 0 .

  T = 0

  
  

  • 4.2)    для нелинейно вязкой среды по модели Оствальда–Вейля (см., например, [2])

  
  

  ^σξϕ

  
  

  = bD ξϕ D^{m - 1},

  
  

  • 4.3)    для вязкопластической среды по модели Бингама (см., например, [3])

  _CT = / 1 + Bm/DD>& ПРИ D "  D 0 , ^fp [ k _a D ^        при D <  D 0 ,

  
  

  P = - _{ξ 02} A σ ξϕ _{ξ = ξ 0}

  
  

  = ^{∂ U} - ^U   = ^{MR 2}

  ^{ξϕ =} ∂ ξ ^- ξ ^{, =} 2 K

  
  

  Bm = σ ⁰ , b = ^{q 0 m 1 Kv} , D 0 = ^Bm , v ρ q ₀         v ρ          k _σ - 1

  
  

  U = V dq ₀ , T = q ₀ t , ξ ₀ = R / d , ξ = r / d , d = v / q ₀ , q ₀ = 2 π / τ ₀, ∆ ₀ = δ ₀ /2 π ;

  
  
  
  

t – время, α – угловое смещение цилиндра, α ₀ – начальное смещение, R – внутренний радиус цилиндра, d – толщина пограничного слоя, K_v и m – постоянная и показатель степенного реологического закона, Bm – число Бингама, σ ₀ – предел текучести, ν – кинематическая вязкость среды, ρ – плотность среды, V ( r , t ) – азимутальная компонента скорости , τ ₀ – период собственных установившихся колебаний, q ₀ – циклическая частота колебаний пустого цилиндра, δ ₀ – логарифмический декремент затухания собственных установившихся колебаний, D _ξϕ – ξϕ -я компонента D , D – второй инвариант D , D – тензор скоростей деформации, σ _ξϕ – ξϕ -я компонента тензора напряжений; P – момент сил, приложенных к цилиндру со стороны среды, A – отношение моментов инерции среды в цилиндре 0,5 MR ² и пустой подвесной системы K относительно оси цилиндра, M – масса среды, величины P , M и K отнесены к единице длины цилиндра. Для рассматриваемого течения D = D _ξϕ . При моделировании вязкопластического поведения в (6) принята модель bi-viscosity, в которой для лучшего соответствия модели истинному вязкопластичному поведению модельный коэффициент k _σ ~ 10³ . Затуханием колебаний в отсутствие среды далее пренебрегаем: δ ₀ = 0.

Вибрационный метод

Математическую модель вискозиметрических экспериментов представим как

∂ U ∂ T

_∂ 2 _U

₂ ⋅ k f ; ∂ z

² x       T    ∂ U

+ x = sin + 2 A λ ∂ z

^{⋅ k} tr ^;

z = 0

dx / dT _{T = 0} = 0, x (0) = 0, U ( z ,0) = 0, U (0, T ) = y ⋅ dx / dT , U ( ∞ , T ) = 0;

для среды Оствальда–Вейля:

m - 1                       ^{m -} 1

k_f = mb ∂ U / ∂ z    , k_tr = b ∂ U / ∂ z _{z = 0} ;

для среды Бингама:

kf = k r = ka - при |d UI dz| < D0, kf = 1, kr = (1 + Bm I|dUI dz||_ ^ - при |dUI dz| > D0;           (12)

где x = xk IF , T = to ₀ 1 , X = to ₀! to , to^ = k I m ₀, z = z I d , d = ^v I to ₀ , A = Sv pm ₀ 1F , b = to™ ^{- 1} K_v I(v p ) , Bm = < r ₀ 1(v pto ₀ ), у = F I(kd ), U = VI(d to₀) , V = V_x - скорость колеблющейся пластины, m ₀ - масса подвесной системы, k - жесткость упругого элемента, to и F - частота и амплитуда вынуждающей силы, S - площадь поверхности пластины, x - линейное смещение пластины, z - координата вдоль оси Z , z = 0 - на пластине; в = -/2 Ay , где в - см. [2]; описание остальных параметров - см. после (7).

Сопряженные задачи о движении зонда и среды (1)-(3), (5) или (6) и (8)-(10), (11) или (12) решены численно. Для решения системы нелинейных уравнений в работе использован метод прямых. Полученная система обыкновенных дифференциальных уравнений интегрировалась, в частности, методом Рунге-Кутта четвертого порядка с контролем точности и автоматическим выбором шага по времени, методом Адамса пятого порядка точности в форме Нордсика и пр. Для интегрирования жестких систем, возникающих при определенных условиях эксперимента, был использован метод Гира шестого порядка точности. Производные по координате аппроксимировались разностными отношениями с пятью узловыми точками, обеспечивающими точность порядка четвертой степени шага по координате.

Результаты и обсуждение

Нелинейно вязкие среды

Рассмотрим простейший тип осциллирующего течения - на пластине. Для нелинейно вязких сред можно выделить два вида течения: при вязкости больше и меньше ньютоновской, в зависимости от чего граница области развитого течения приближается или удаляется от пластины по сравнению с ньютоновской (рис. 3 - для дилатантной среды). Это объясняется тем, что глубина проникновения пропорциональна кажущейся вязкости bD m ^{- 1}, определяемой отношением напряжения и скорости сдвига, которая для дилатантных сред при данных условиях эксперимента (когда D <  1) падает с ростом m и при уменьшении D . Так, рис. 3б соответствует малым D ( D '₀| <  0.1, где D '₀ = D'| z , D' - скорость сдвига). Кривая течения для m = 2 на рис. 3а проходит ниже прямой для ньютоновская среды с m = 1, и граница области, где U ~ 0, находится ближе к пластине для среды с m = 2. При в = const с ростом у , т.е. с ростом, например, амплитуды вынуждающей силы F , расширяется интервал значений скорости сдвига, проходимых в процессе колебаний, и при D '₀| >>  1 граница находится существенно дальше от пластины, чем для ньютоновской жидкости. На практике это может означать, что предположение о безграничности среды уже не допустимо и влиянием стенок пренебрегать нельзя.

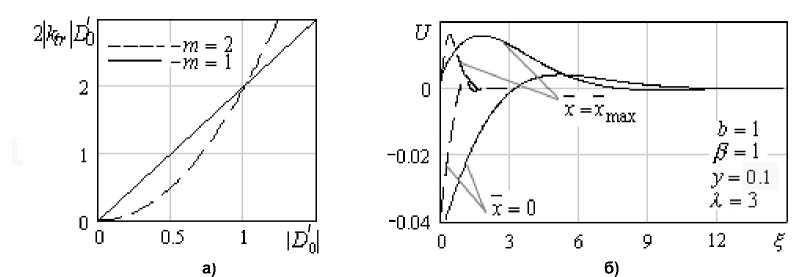
Рис. 3. К зависимости U = U ( Z ) для дилатантной среды при малых скоростях сдвига

На частотных спектрах напряжения и скорости сдвига на пластине (рис. 4), построенных для режима установившихся колебаний, выявлено появление нечетных гармоник вынуждающей силы, обнаруженных ранее в [4] в упрощенной модели с сосредоточенными параметрами. Распределение интенсивностей пиков спектра, в т.ч. вид их огибающей, определяется нелинейными свойствами жидкости и условиями эксперимента, что позволяет исследовать свойства таких сред в рамках Фурье реологии.

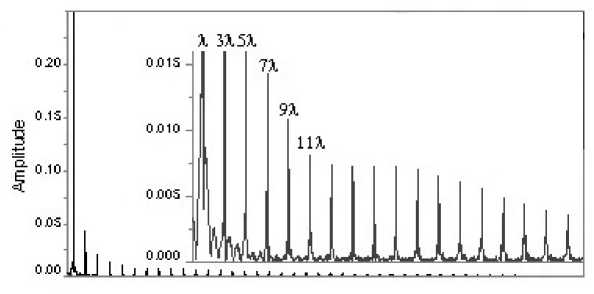
а) б)

Рис. 4. Спектр (а) и зависимость скорости сдвига (б) на пластине от времени

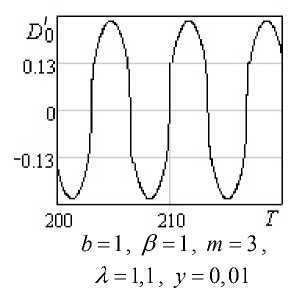
Данные особенности наблюдаются и при течении в крутильно-колебательном вискозиметре. Заметим, что в т.ч. при малых скоростях сдвига, реализуемых в режиме затухающих колебаний, среды с m >  1 относятся к дилатантным, а с 0 <  m <  1 – к псевдопластичным. При численном моделировании с учетом того, что для дилатантных сред область развитого течения находится вблизи стенки цилиндра, расчеты необходимо проводить в интервале ξ ∈ [ ξ ₁, ξ ₀], где ξ ₁ определяется как U (0 … ξ ₁, T ) ~ 0, а для псевдопластичных – в ряде случаев брать большее число точек у оси цилиндра.

Вязкопластичные среды

При заполнении крутильно-колебательного вискозиметра вязкопластичной средой около оси цилиндра всегда присутствует твердое ядро (зона 1 на рис. 5), где сдвиговые напряжения не превосходят предел текучести. Также в потоке имеется тонкая твердотельная прослойка (зона 2 на рис. 5), возникающая у поверхности цилиндра, перемещающаяся в процессе колебания к ядру, граница которого движется в это время от центра, и при достижении ядра сливающаяся с ним (рис. 5–7). В таких зонах скорость U по координате ξ изменяется линейно: dU / d ξ - U / ξ = 0, и, в частности, в случае развитого по всему сечению твердотельного течения U ( ξ , T ) = d α / dT ⋅ ξ . Застойным зонам соответствуют прямолинейные участки, начиная от ξ = 0, на рис. 6, 7 (зона 1) и искривление профиля скорости сдвига при смене знака D ' на рис. 7 (зона 2); это области с D ' <  D ₀ на рис. 5.

Расчет по идеальной модели для вязкопластичной среды (т.е. когда σ _ξϕ = D _ξϕ = 0 при ^σξϕ <  σ ₀ в (6) и пр.), так же как и учет конечной длины цилиндра, значительно усложняет численные формулировки, в т.ч., существенно повышая время расчета, и в то же время не обеспечивает требуемой точности и в ряде случаев сходимости к истинному решению. Так, например, численные модели, основанные на определении на каждом временном слое радиуса твердого ядра вязкопластического течения аналогично выполняемому при стационарных течениях, к примеру, в капиллярной реометрии, не позволяют корректно промоделировать твердотельные прослойки, наличие которых изменяет напряжение на стенке цилиндра, внося часто существенные ошибки в закон колебаний. Использование модели bi-viscosity здесь дает удовлетворительные результаты: при k _σ ~10³… k _σ ~10⁴ расхождение в рассчитанных значениях составляет менее 0,1 %.

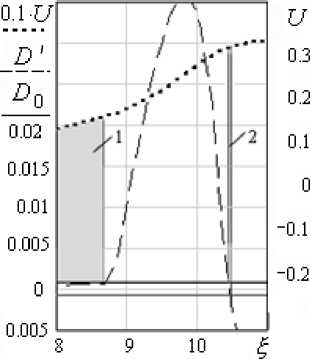
Рис. 5. Зависимости

U = U ® и D = D £ )

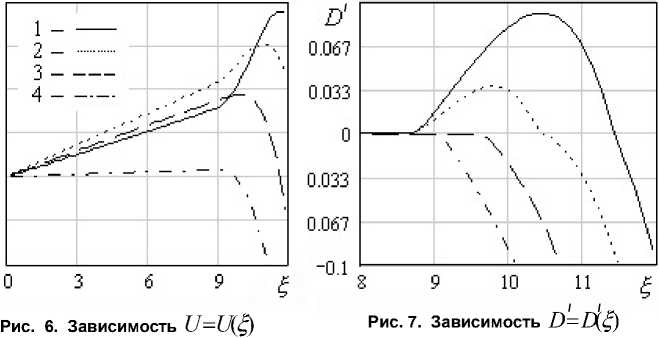
^ 0 = 12 , A = 0,2 , Bm = 0,4 ;

Кривые 1–4 соответствуют моментам времени в течение 1-й четверти полупериода (крив. 1, 2) и 2-й четверти (крив. 3, 4)

– застойные зоны

При течении в вибрационном вискозиметре при значениях z , прилегающих к правой границе расчетной области, образуется неподвижная твердотельная зона, а вязкопластическое течение перемежается твердотельными прослойками (обычно 1-й – 2-мя). Для такой жидкости характерен рост области развитого течения по сравнению с ньютоновской (т.е. смещения расчетной границы U ( ” , T ) = 0 в (10)) вследствие увлечения жидкости твердыми прослойками, что качественно согласуется с результатами для псевдопластичных сред.

Заключение

В работе обсуждены особенности, на которые следует обращать внимание при численном моделировании экспериментов по идентификации реологической принадлежности и свойств неньютоновских сред – нелинейно вязких (модель Оствальда–Вейля) и вязкопластичных (модель Бингама). Так,

• 1)    выявлен рост области развитого течения для вязкопластичных и псевдопластичных жидкостей и уменьшение этой области для дилатантных сред;

• 2)    проанализирована динамика развития твердотельных зон в процессе затухания крутильных колебаний,

• 3)    установлено появление нечетных гармоник вынуждающей силы на спектрах напряжения и скорости сдвига на пластине;

• 4)    выполнены рекомендации по численным расчетам таких течений в осциллирующих рео-метрических системах.