Особенности тока смещения флуксона в неупорядоченном S-I-S-туннельном контакте

DOI:

Динамика джозефсоновских вихрей (флуксонов) в туннельных структурах различных видов [1; 2; 8] в настоящее время представляет предмет неослабевающего интереса как с теоретической, так и с экспериментальной и технической точек зрения (см., например, работы [4; 5; 13–18]), в том числе и в связи с перспективами применения в качестве элементов вычислительных устройств новых типов [14; 18]. При движении флуксона в туннельном S-I-S -контакте, в I -слое которого присутствуют случайные неоднородности (микрозакоротки, сужения и др.), радиационное трение вихря об эти неоднородности приводит к замедлению его движения и остановке – осуществляется «пришпиливание» (пиннинг) флуксона. Для управления скоростью движения флуксона можно ввести в контакт ток – так называемый ток смещения флуксона [19], пересекающий плоскость контакта.

В работе [5] в качестве неоднородности, влияющей на динамику вихря в длинном S-I-S -контакте, рассматриваются случайно образующиеся в содержащем примесные атомы I -слое квантовые резонансно-перколяционные траектории [6; 9].

Приведем кратко основные сведения о квантовых резонансно-перколяционных траекториях. Рассмотрим явление туннелирования электронов через случайно-неоднородный слой, в качестве модели которого выберем прямоугольный потенциальный барьер высотой U 0 , возмущенный расположенными случайным образом одинаковыми локализованными потенциальными ямами, образованными примесями. Если энергия туннелирующей частицы значительно меньше высоты барьера, то радиус локализации электронного состояния на примеси будет намного меньше расстояния между примесями. При этом процесс туннелирования даже при рассмотрении трехмерного барьера сохраняет многие черты одномерности, поскольку из-за сильного затухания в подбарьерной области траектории частиц будут сосредоточены внутри цилиндров с радиусом, равным радиусу локализации. Если энергия налетающих частиц ε не попадает в область энергий туннельных резонансов для данного барьера, то происходит нерезонансное туннелирование. Если же энергия налетающих частиц попадает в эту область, то может осуществиться резонансное туннелирование. В работе [9] показано, что в этом случае при всех значениях энергии существуют маловероятные конфигурации примесных центров, которые приводят к возникновению образований, названных авторами работы квантовыми резонансно-перколяционными траекториями (КРПТ). Такие траектории являются путями, по которым частицы могут туннелировать с коэффициентом прохождения, близким к единице. Нерезонансная прозрачность типичных барьеров чрезвычайно мала, поэтому вероятность реализации резонансных конфигураций и их энергетические ширины в значительной степени определяют среднюю прозрачность слоя. Пространственная структура уединенной КРПТ схематично представлена на рисунке 1.

В работе [6] получено общее выражение для локальной прозрачности при рассмотрении прохождения частицы через m -примесную КРПТ в трехмерном неупорядоченном барьере:

ВДе - е₀ , q , р ,«) = 4а₀^ exp [ -^{а р р} ' - ^П^ - 1 , (1) fc n a Y 2

где q - поперечная компонента импульса частицы на входе в барьер; р = (у, z) -поперечная координата частицы на выходе из барьера; tf ₀ = a ² k ² /(2n(a ² + к²))² ; к² = = е ( к/(2m) = 1); k_q = V е — д ² ; a = у/U 0 — е ; е ₀ - уровень энергии примеси; р _т -

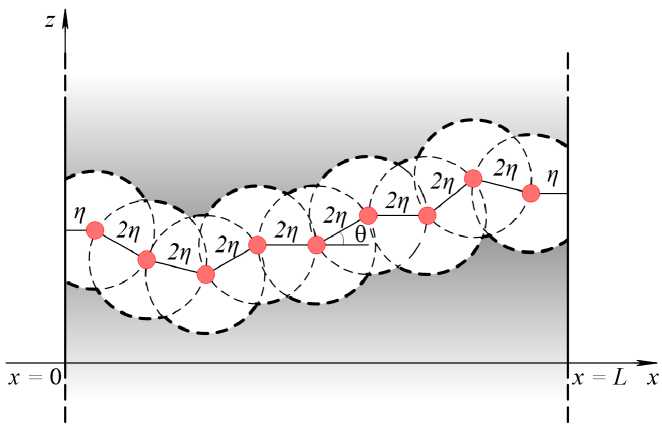
Рис. 1. Пространственная структура уединенной КРПТ. Заштрихованными кружками обозначены примеси, расположенные в узлах ломаной линии с шагом 2 η поперечная координата т -й (последней в КРПТ) примеси; и = 2ап — безразмерный шаг КРПТ; 2п — расстояние между примесями; y = 4а ² и ^{- 1} е ^-и - энергетическая ширина зоны резонансной прозрачности.

В отличие от классических закороток (тонких сквозных перемычек между S -берегами контакта) КРПТ, коэффициент прохождения вдоль которых близок к единице, и вдоль которых, соответственно, может возникать ток, приводят к появлению закороток иного типа – квантовых.

В I -слое реальных контактов примесные атомы присутствуют неизбежно, поэтому задача описания динамики флуксона и управления его движением в таких контактах интересна и актуальна.

В данной работе на основании теории, развитой в [5; 6; 9], показано, что ток смещения флуксона, как функция энергии туннелирующих через плоскость контакта электронов и концентрации примесных атомов в I -слое, имеет особенности (дополнительные максимумы), связанные с туннелированием через примесные конфигурации, составленные разным числом атомов, а также что зависимость тока смещения от энергии туннелирующих электронов при изменении концентрации меняется не только количественно, но и качественным образом. Поведение тока смещения исследовалось численно-аналитическим методом. Метод в различных его вариациях успешно применяется при решении широчайшего спектра задач, возникающих в естественных науках и технических приложениях – см., например, [7; 11; 12], в том числе и в задачах, близких по тематике к данной работе: [20].

1.    Модель. Основные соотношения

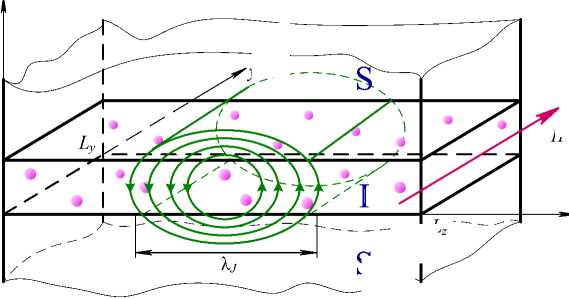
Рассматривается модель S-I-S -туннельного контакта, состоящего из двух массивных сверхпроводящих электродов с одними и теми же свойствами, разделенных плоским длинным L _z ^ Л у узким L _y ^ Л у ( А _; - джозефсоновская глубина проникновения) слоем изолятора толщиной L _x (см. рис. 2). Контакт помещен при температуре Т = 0 в параллельное плоскости контакта магнитное поле (0,Н _у , 0) . Барьерный потенциал

x

L x

y

I

——

H

z

S

Рис. 2. Джозефсоновский контакт с примесями в I -слое, помещенный в параллельное плоскости контакта магнитное поле (0 ,Н _у , 0) . Характерный размер флуксона порядка X j

I -слоя без учета влияния примесей U 0 = const > ц , где ^ - уровень Ферми контакта. В слое изолятора случайным образом распределены одинаковые, притягивающие электроны немагнитные примеси, имеющие энергию однопримесного локального уровня ε ₀ и радиус локализации электронного состояния на нем а ^{- 1} = (U 0 — е ₀) ^{- 1 / 2} (используется система единиц, в которой h = 1 , масса и заряд электрона т = 1/2 , е = 1 ). Большое число ( N ^ 1 ) примесей макроскопически однородно распределено с плотностью п = N/V по объему слоя: V = LS ( L = L _x - толщина слоя изолятора, S = L _y L _z -его площадь). Рассматриваются значения безразмерной концентрации с = па - 3 ^ 1 , то есть случай слабого структурного беспорядка.

Ток смещения флуксона в контакте с неупорядоченным I -слоем определяется следующим образом [5]:

L

(пА ^{3 / 2} ®(в) /                  f А

3 ⁼\~2~)    L ^{д⁽⁵’^С^    Z^^fm ^{( 5,} с).

'           V              т=1

где 5 = ц — Е ₀ ; А - ширина энергетической щели сверхпроводника S .

{ д^.с) = £g;_n"(S,c)

т

-

среднее значение туннельного через (1) и имеют вид:

кондактанса контакта, а д^^с), ^(Ъ.с) вычисляются

В (4), (5)

д^.с)

f m ^es (5.c)

∞

= ^ 0 У Р т ( ^с . ^и )е^хр (- Y^du.

∞

= ^ff 0 ^ Р т ^{( с} . ^{u ) ex}P ( ^— Y2~) ^du.

Р т (с. U) = а ² с ^т е

^стпи 3 [ м ² 0 ² (т.м) ] ^т 1

-

вероятность (на единицу площади контакта) образования уединенной m-примесной квантовой закоротки с шагом и, в (m,u)= [2 (^ - 1)f « 1 - угол, характеризующий извилистость квантовой закоротки, yJu) = 4а2и-1е-и - ширина зоны резонансной прозрачности вдоль m-примесной КРПТ с шагом и,

®(в) = [71 - ^] е—П/в’ в = v/c0; v - скорость флуксона, пропорциональная напряжению на контакте; с0 -скорость Свихарта.

• 2.    Исследование энергетической зависимости тока смещения флуксона

Проанализируем поведение вкладов m -примесных КРПТ в ток смещения флуксона и суммарного тока в пространстве параметров (5, с) .

Вклад однопримесных квантовых закороток ( m = 1 ) определяется следующим образом [5]:

Л = ®(в)

л^0 А 3/2     1/2

(             <^ > ^{1 / 2} ас exp

^{L -} Y^Lj ] •

В случае квантовых закороток с m >  1 начинает играть роль извилистость траекторий, и их вклады в ток, соответственно, оказываются сложнее для вычисления.

Подынтегральные выражения в (4), (5) как функции аргумента и экспоненциально быстро убывают при удалении от нижнего предела и = u _min , следовательно значение интеграла набирается при значениях и , близких к u min , и при каждом фиксированном значении m главный вклад в (4), (5) дают наиболее вероятные - слабоизвилистые квантовые закоротки, длина которых близка к длине кратчайшей закоротки с шагом и_{1 П}ш = aL/m и, соответственно, наибольшей (при данном m ) энергетической шириной Y _m = 4а ² (aL/m) ^{- 1} exp( - aL/m) .

Учитывая это обстоятельство, представим с высокой точностью формулы (4), (5) в виде

δ2

Cs(5,c) = e ^- ' Р _т (с),                                (11)

2δ2

Ш5,с) = e - ' P _m (c),                             (12)

где

∞ рт(с) = °о У рт(с,и¥и-

Подставляя (6), (7) и интегрируя, получаем

Р п (c) =         E ( - 1) ‘ С П - 1 (:      (rnne)^ ^-1^ x

3                 aL k=0

x _г Г ^{3(m —} 1)^{— к} + 1 ,_ ⁽ OL A ³ 1 , (14)

• 3               \^m / .

где С П - биномиальные коэффициенты,

∞

Г(в,а) = У e ^-t t ^s-1 dt а

-

верхняя неполная гамма-функция [3]. Пользуясь формулой

Г(з + п, а) = Г(5 + п) ^ + а * ^{+ п- 1} е ^-а £ „ Ч ., ,        (16)

ВД           7=0 ^гЧ + ^{п -} J)

где п = 1, 2,... , можно для любых m и к выразить все неполные гамма-функции в (14) через Г(1/3, mnc(aL/m) ³), Г(2/3, mnc(aL/m)³) и exp ( — mnc(aL/m) ³). Общее выражение получается громоздким, поэтому приведем результат для квантовых закороток с m = 2, 3 , имеющих в реальных контактах наибольшие вероятности возникновения:

Р^^ W^ (Ч)^ 3,2пс (^ ] ,        ⁽¹⁷⁾

4a ² c ³     f 4        _7/3 / lL- ² Г 1      (lL\ ³'

^p 3 ^{( c )} = —^x ..^3п ^т) Ч,^3пт) г

• + ₃(3ncm [ ₃,3ПС⁽^ ] — ₃(3пс) - 2 ⁽        — 3ПС⁽^ ]} . (18)

Особенности зависимости от 5 вкладов m -примесных КРПТ определяются условием равенства нулю производной m -го члена суммы в формуле (2)

^ = А • S •(д') 3/2 • fm £( — — —) д^с),(19)

77            1

и производной суммарного тока (2)

= А • 5 • (д)-3/2 £ (Ч — 4-) g„(5,c)f,„(5,c),

°5                    т,п \'«'

где А = (п^/2')3/2/Ly. Из (19), (20) видно, что как для m-примесного вклада, так и для суммарного тока особенности при 5 = 0 будут существовать при любом с, то есть на плоскости параметров (5, с) они образуют прямую 5 = 0. При 5 = 0 множество точек, в которых присутствуют особенности по 5 зависимостей jm(5, с) и j(5, с), будут определяться, соответственно, выражениями

Е(i - 4) ■■ 5, п \ Уп

Е^ .12 -  "ЪЛМЛЛМ = °.

т.п Y'n

С учетом (11), (12) представим (22) в виде

Е f А - 4) ададехр U4 + V] = 0.

тп ^Y п    ^Y т                        ^Y п

Для малых 5 ( 5 ^ у _т , т = 1, 2,... ) можно преобразовать (23) к

1^/ 7    4    7 \

5 2 Е ^Р (с) + з Е + T2TJ + 74 ^ т (с)Р п (с) =

_ т=1 У т         ° т<п ^Y тп    У т У п    У п /

= ^Е У Р т (С + Е f У + А ) Р т (с)Р п (с). (24) т =1 ‘ ^т          т<п ^Y 'm    ^Y n/

В уравнении (24) как множитель при δ ² в левой части, так и правая часть положительны, поэтому найдется такое значение с , при котором оно имеет два различных корня. Множитель при 5 ² и правая часть непрерывны по с и, следовательно, корни уравнения (24) будут меняться непрерывно (оставаясь при этом вещественными) при непрерывном изменении с [10]. Таким образом, при выполнении условия 5 ^ у _т , т = 1, 2,... эти корни будут при некотором интервале значений с образовывать непрерывные отрезки линий на плоскости параметров (5, с) . Следовательно, особенности будут проявляться в некотором интервале значений с .

Тип особых точек будет определяться знаком второй производной

42 = А • ( д^{( 5,с )} ) ^{- 3 / 2} ЕГ -1 2 ^- Л ) з п ^{( 5,с )}/ т ^{( 5,с ) -}

• ⁵                          т.п ^Y '^п     ' ^т'

• ^{- А5 2}у ^{( 5,с)}у ^{5 / 2} Е f 4 — 4 )f ^2 -   -    )з п ^{( 5,с )} 3 к ^{( 5 ,с)}/ т ^{( 5 ,с) (25)}

т.п.к ^{Y Vn     У т}' ^{Y Vn     Y k     У т}'

для суммарного тока смещения, и аналогичным выражением, но с фиксированным т для вклада т -примесных КРПТ. При 5 ^ 0 из (25) и из (21), (22) получаются совпадающие в пределе выражения для т -примесных вкладов и суммарного тока, поэтому вдоль 5 = 0 изменение типа экстремума будет происходить при переходе через точку, к которой подходят линии особенностей при 5 = 0 .

Аналитическое вычисление корней даже в частном случае 5 ^ у _т затруднительно ввиду сложной зависимости Р _т (с) , поэтому поведение суммарного тока и его вкладов на плоскости (5, с) при типичных значениях характеристик контакта исследовалось численно.

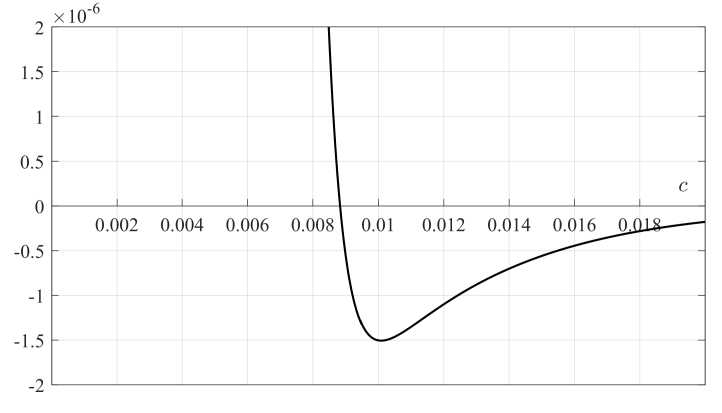
Рис. 3. К нахождению решения уравнения (26)

На рисунке 3 приведен результат численного решения уравнения

Е -Т - 72 p , W=«                     (26)

n=1 ^Yn   Y2/ при типичных значениях параметров контакта aL = 9, U0 = 10 эВ, ц =5 эВ для случая двупримесного вклада при учете влияния возникающих с наибольшими вероятностями КРПТ ст = 1, 2, 3. Конфигурация линий особенностей при 5 = 0 и 5 = 0 для двупримесного вклада показана на рисунке 5б, на нем видно, что линии особенностей при с = 0 примыкают к прямой 5 = 0 в той же точке (с ~ 0, 0087), в которой при 5 = 0 изменяется тип особенности (минимум сменяется максимумом в направлении возрастания с). Результаты аналогичных расчетов для трехпримесного вклада и суммарного тока смещения приведены на рисунках 6б, 7б.

3.    Численное исследование особенностей тока смещения

Подход к получению результатов предполагал следующие два этапа. Первый – проведение аналитических вычислений до того предела, когда дальнейшее продвижение становится уже нецелесообразным из-за сложности и громоздкости получаемых выражений, и второй – использование компьютерного моделирования для анализа полученных результатов. В рамках первого этапа получен легко принципиальный результат – показано, что для S-I-S -контакта с квантовыми закоротками в I -слое обязательно существует некоторый диапазон концентраций, при которых ток смещения флуксона как функция разности δ между уровнем ферми контакта и энергией налетающей частицы будет при малых величинах этого отклонения ( 5 ^ у _т , т = 1, 2,... ) иметь особенности, описываемые уравнениями (24), (25). На втором этапе использование компьютерного моделирования позволило найти эти значения концентрации, а также исследовать зависимость j (5, с) уже без ограничений на значения 5 . Моделирование показало, что для типичных параметров контакта существует широкий диапазон концентраций с , при которых зависимость j (5, с) от 5 имеет множественные максимумы, ассоциированные с т -примесными КРПТ.

Для проведения численных расчетов использовался программный пакет GNU Octave. При исследовании поведения j(5, с) , а также вкладов КРПТ, шаг изменения 5 был выбран равным 0,02у 1 . Неполные гамма-функции в (17), (18) вычислялись с помощью

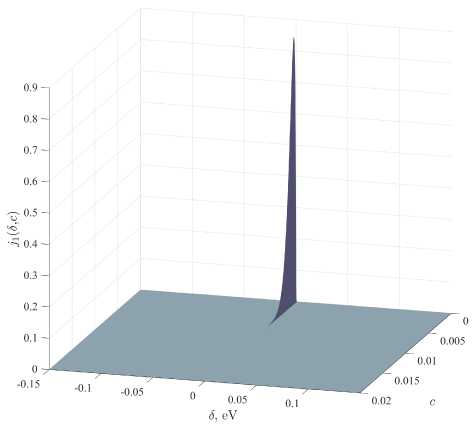
Рис. 4. Однопримесный вклад в ток смещения: график j 1 ( 5, с ) встроенных функций GNU Octave. Проверка прямым численным интегрированием показала адекватность работы этих встроенных функций при фигурирующих в расчетах значениях безразмерной концентрации с и при рассматриваемых характерных значениях параметров контакта.

Результаты численных расчетов j _m (5, с) для т = 1,2,3 и суммарного тока j (5, с) , проведенных для характерных значений aL = 9 , U 0 = 10 эВ, ц = 5 эВ, приведены на рисунках 4-8. Рисунки 4, 5, 6 иллюстрируют поведение т -примесных вкладов в ток j _m (5, с) ( т = 1,2,3 ). Видно качественное изменение зависимости при учете т >  1 : появляются новые особенности, отстоящие от локального однопримесного электронного уровня е ₀ на величину порядка Y _m • На рисунках 5б, 6б сплошные линии составлены точками, в которых dj _m /д 5 = 0 , синим цветом закрашены области, в которых д ² j _m /д 5 2 < 0 , зеленым - в которых д ² j _m /д 5 ² > 0 . На рисунке 7б используется та же схема для выделения линий дj/д 5 = 0 и знака д ² j/д 5 ² . На рисунках 4, 5а, 6а, 7а, 8 величина вкладов в ток смещения и суммарный ток нормированы на максимальную величину суммарного тока, поэтому множители, не зависящие от 5 , с в (2), не оказывают влияния на результаты. Значения с , соответствующие решениям уравнения (24), при указанных значениях параметров контакта, лежат в диапазоне с = 0, 0089 ... 0, 0092 .

Из рисунка 8 видно изменение зависимости j (5, с) при изменении с : при самых низких концентрациях существенен лишь однопримесный вклад (график 1), далее однопримесный вклад становится больше, и параллельно «включается» двупримесный, при этом возникают дополнительные экстремумы (график 2), затем «включается» трехпримесный вклад, что также отмечается появлением дополнительных экстремумов (графики 3, 4). При дальнейшем увеличении с влияние КРПТ уменьшается, а дополнительные экстремумы сглаживаются и исчезают (графики 5, 6).

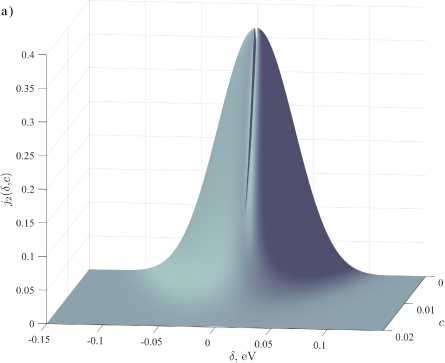
Рис. 5. Двупримесный вклад в ток смещения: а) график j ₂ ( 6, с ) ; б) особенности двупримесного вклада в ток смещения

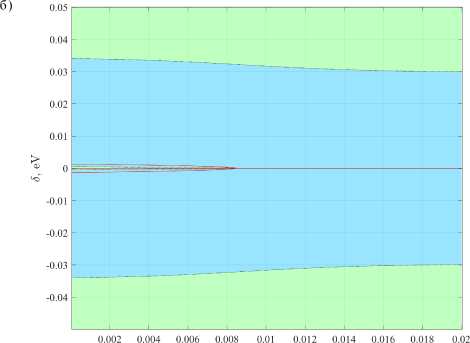
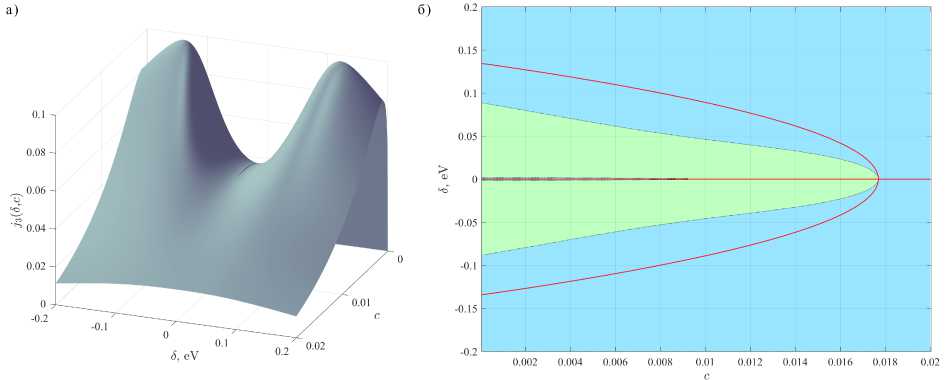
Рис. 6. Трехпримесный вклад в ток смещения: а) график j ₃ ( 6, с ) ; б) особенности трехпримесного вклада в ток смещения

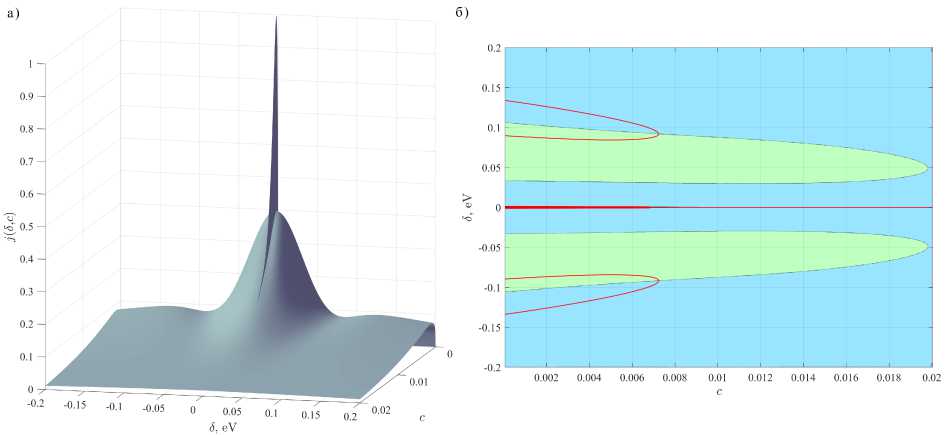
Рис. 7. Суммарный ток смещения: а) график j ( 5, с ) ; б) особенности суммарного тока смещения

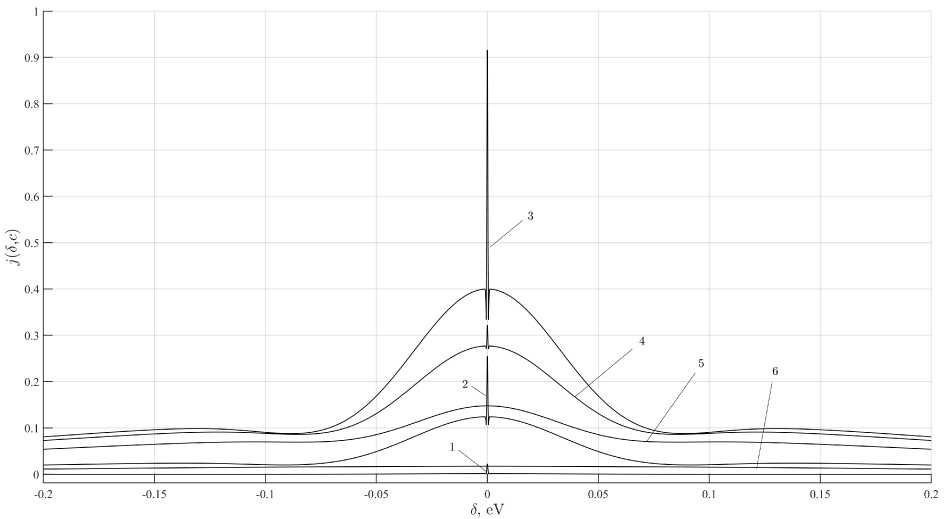
Рис. 8. Зависимость j (5 , с ) при с = 10 ⁷ (1), с = 10 ⁵ (2), с = 9 • 10 ⁵ (3), с = 3 • 10 ³ (4), с = 6 • 10 -3 (5), с = 0 , 02 (6)

Заключение

В работе исследовано поведение тока смещения флуксона в длинном джозефсонов-ском S-I-S -туннельном контакте с неупорядоченным I -слоем в пространстве параметров (5,с) , где 5 = ^ — £ 0 - отклонение уровня Ферми контакта от локального одноэлектронного примесного уровня. Показано, что есть физически существенные значения концентрации, при которых зависимость тока смещения от δ имеет особенности (дополнительные максимумы), обусловленные вкладами КРПТ, проходящих через разное число примесей. Также выявлено не только количественное, но и качественное (появление и исчезновение особенностей) изменение зависимости тока смещения флуксона от δ . Полученные результаты могут быть полезны при интерпретации данных возможных экспериментов, а также при создании технических устройств на основе неупорядоченных S-I-S -контактов.