Особенности вертикальной прокатки упруго-вязких материалов

При производстве шлифовального инструмента применяемого особенно широко в авто, авиа, моторостроении используется гетерогенная, упруго-вязкая масса из смеси упруго-вязкого каучука с жестким недеформируемым абразивным зерном, обладающая в процессе обработки давлением деформационным упрочнением и значительной упругой деформацией [1]. Прокатка таких материалов в промышленном производстве происходит в двухвалковом очаге деформации образованном валками, оси которых находятся в одной горизонтальной плоскости, а прокат расположен в вертикальной плоскости. К геометрическому очагу деформации (рис. 1) протяженностью l_r , как отмечено в работе [2], примыкает зона l ₁ эластического восстановления размеров проката. При задаче в валки с помощью подъемника большой массы кусковой абразивной смеси, до геометрического очага деформации будут расположены зона подачи кусковой массы в валки и зона предварительного уплотнения l ₀ . Зона подачи h _п ограничена стенками загрузочного бункера. В этой зоне при высокой адгезии кусков смеси к валкам и действии массовых сил будет осуществляться процесс начального уплотнения кусков вулканитовой смеси. При безбункерной подаче кусков абразивной смеси в валки, например, с помощью загрузочного транспортера, зона подачи отсутствует. Эти два варианта процесса прокатки будут отличаться в первом случае наличием подпирающей силы T ₀ в зоне подачи на смесь в очаге деформации от действия массы загрузки.

Полный или фактический очаг деформации, кроме линейных размеров ( l ₀ , l_r , и l ₁ ), может быть определен значениями углов а _п = а ₀ +а r + а 1 , где а ₀ - угол, определяющий зону предварительного уплотнения; а r - угол, определяющий геометрический очаг деформации; а 1 - угол, определяющий зону эластического восстановления размеров проката [3].

Показанная на рис. 1 схема прокатки позволяет определить геометрические параметры полного очага деформации протяженностью l _п и подсчитать вертикальную проекцию площади контакта вулканитовой смеси с валками:

F = I п b l = ( 1 0 + i r + 1 1 ) b l, (1)

где b ₁ – ширина листового полуфабриката.

По известным в теории прокатки металлических материалов зависимостям [4] можно подсчитать параметры геометрического очага пластической деформации:

l r =V ( h o - h b ) R ;

^а r

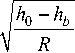
Протяженность зон АА1В1В и ДД1Е1Е (рис. 1 и 2) определяется из следующих выражений:

• l0    = V( hп — hb ) R — 4( ho — hb ) R ;

• 1 1    =V ( h l - h b ) R .

  

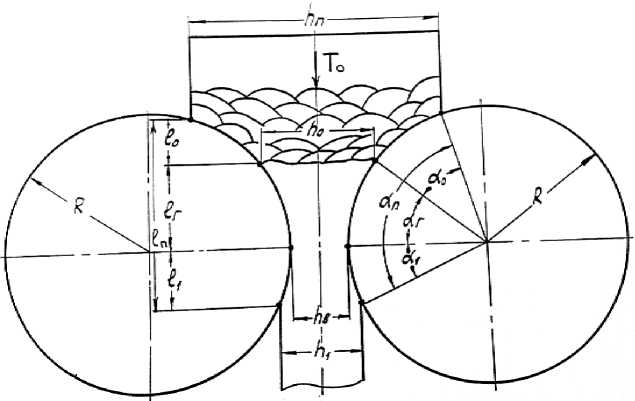
  Рис. 1. Схема прокатки абразивной смеси в двухвалковой клети

  
  
  

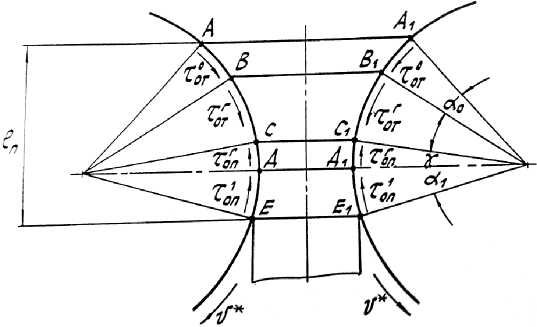
  Рис. 2. Схема действия кинематических и силовых параметров в очаге деформации при двухвалковой прокатке

  
  

В з оне пред вари те л ьн о г о у пл о т нен ия им е ет ме с т о з начител ьно е на руш е ние сп л ош ности, возникающее из-за не ра вном е рного пос ту пл ен ия кус ковой аб раз и в н о й см е с и, п о эт ом у з ап ише м в ыр а жен и е (1) дл я на хож ден ия по л ной п л оща д и кон та к т а с учет ом ко эффициента не с п л ошнос т и k :

F n = kF o + F r + F i , (6) где F _o = 1 0 b 1 , F r = 1_rb_r , F 1 = 1 1 b 1 - соответственно в ер ти к а л ь ные про е к ци и п л оща де й з он АА 1 В 1 В, ВВ 1 Д 1 Д, ДД 1 Е 1 Е.

П ри экспе рим е н т ал ьны х исс л едова н ия х у с т ановлено, что для случая ков шовой за груз к и k = 0,8, а при транспортерной загрузке k = 0, 65.

И с по л ьзу я в ыра жен ия (2), (4) и (5) дл я на хождения значений l ₀ , l_r и l ₁ , имеем

F = b JR x

x [k4hп - hb + (1 - k) 4ho - hb + 4hi - hb ]. (7)

Пр и ве д ен н ы е в р аб от е [ 2 ] э к с п ер и м ен та ль ны е и ссле д о в ан и я ск о р о стн ы х у с ло вий п р о ц есс а пр о ка тк и п о зв оли ли п р е д л о жи т ь сле ду ю щую к и нем ат и ч еск у ю мо д ель п олн о г о о ч ага д е фо рм а ц и и .

Как видно из рис. 2 в зоне АА 1 В 1 В скорость валков и * значительно превышает скорость перемещения вулканитовой смеси и _п и поэтому удельные силы 0

трения со стороны валков т от , направленные по ходу прокатки, втягивают смесь в зазор между валками. На части геометрического очага деформации (зона ВВ 1 С 1 С) скорость валков и * также превышает скорость перемещения смеси и _п и силы трения т от также направлены по ходу прокатки. Используя принятую при прокатке металлов терминологию, можно отметить, что зоны АА₁В₁В и ВВ 1 С 1 С образуют общую зону отставания АА 1 С 1 С. В плоскости СС 1 скорость перемещения полосы становиться равной скорости валков, поэтому эта плоскость является нейтральной.

Скорость полосы превышает скорость валков в зонах СС₁Д₁Д и ДД₁Е₁Е, поэтому удельные силы г1

трения Т от и т от направлены против хода прокатки. Эти две зоны образуют общую зону опережения СС₁Е₁Е.

Для расчета величины опережения воспользуемся формулой, предложенной в работе [2] для процесса двухвалковой прокатки:

i =

^и 1

to R — R ( h i — h b )

Из условия постоянства массы, записанного для критического сечения и плоскости выхода, следует и b py hY = h1p1u1 , где hY, pY - соответственно высота полосы и ее

h_b + 2 R — 2 R ² — R ( h 1 — h b ) h ₁

плотность в критическом сечении. Тогда

Здесь to - окружная скорость валков; е 1 - коэффициент изменения плотности в зоне ДД 1 Е 1 Е,

e_x = ln — /ln —, 1       P i /     h b

h (17) и p y

Учитывая равенство (16), имеем hy=( i +1) h1^.                             (18)

^p Y

где p ь и p 1 - соответственно плотность абразивной смеси в плоскости осей валков и в плоскости

Величину pY определим по формуле, приве-

денной в работе [1],

выхода.

Коэффициент изменения плотности деформируемого материала в зоне АА1Д1Д также зависит от изменения высоты очага деформации:

e о = In   /ln h ¹,                          (10)

p ₀      h ₀

p Y = p o

e 0

h ⁰ h

где p ₀ - плотность материала в плоскости ВВ 1 .

Для описания зоны ДД 1 Е 1 Е введем коэффициент эластического восстановления высоты проката:

= h h = h , — 1.                        (11)

^э      h b       h b

Из условия постоянства массы, записанного для плоскостей по осям валков ДД1 и выхода проката из валков ЕЕ1, u b pbhb = h1P1u1 ,                               (12)

Учитывая выражение (9), получаем hY—e0 =( i +1) hl-p1.                           (20)

h ₀ p ₀

Из геометрии очага деформации следует, что hY= 2 R (1 — cos y) + h0.                      (21)

При 1 — cos y = 2sin² ( y /2 ) , когда величина ар-

гумента мала, допустимо упрощение вида 1 — cos y = Y2/2 .

В итоге выражение для определения критиче-

ского угла примет вид

имеем h1 = u b p b hb   UA ’

Y= — ■^(1— e 0)/ ( i +1) -^--^1-

4 R V    h 0 p 0

.

где и b и u 1 - скорости полосы соответственно в плоскостях осей валков ДД₁ и выхода из валков ЕЕ₁.

Приведем выражение (11) для определения коэффициента эластического восстановления с использованием равенства (13) к виду

Для нахождения опережения, в теории прокатки металлов часто используют формулу Головина – Дрездена [4]

R i =TY h1

к э = U b P 6. — 1

^u 1 p 1

Найдем величину критического угла y , деля-

щего очаг деформации на зоны опережения и отставания, используя полученные эксперименталь-

ным путем значения опережения и скорости на выходе из очага деформации. Известно, что экспе-

риментально опережение определяется по зависимости [2]

i =

*

U 1 — и и

^и 1

* и

— 1.

Отсюда следует, что

^:= ( i — 1 ) .                                          (16)

и

которую можно записать и относительно критического угла в следующем виде:

Y = #. ⁽²³⁾

Нетрудно видеть, что зависимость (22) при условии отсутствия эластического восстановления ( h 1 = h b ), условии постоянства плотности ( p ₀ = p 1 , e ₀ = 0) принимает вид формулы Головина - Дрездена.

Для определения момента и мощности на бочке валков используем зависимости, полученные в работе [5].

Силы трения в зонах отставания и опережения создают момент на бочке валка. Эти силы активны в зоне отставания, и за счет их осуществляется процесс деформации, в зоне опережения они реактивны и направлены против хода прокатки.

Момент на бочке валков для рассматриваемого очага деформации можно записать

M В = R 2 b l ( I a - I p ) ,                       (24)

м В = T cp b 1 R R

h

^{- h}b

R

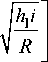
( “ 0

где I_a

= k J

I 0

a r        A a r            y

T xa d «- J t xa d a + J t xa d «- J t xa d a , 0         J    0           0

Y             « 1

ID = [tx_d a + f txdi a.

p xp          xp

Используем теорему о среднем значении интеграла, и на этом основании будем считать, что t _xa ~ t xp ® T cp , тогда выражение (24) преобразует-

Получена формула [5], которую часто используют для нахождения момента на бочке валка при прокатке металлов и сплавов.

Приведенные зависимости позволяют подсчитать параметры, которые достаточны для построения геометрической, кинематической и динамической моделей процесса прокатки вулканитовой абразивной смеси в двухвалковом очаге деформации с вертикальным направлением оси прокатки.

ся к виду

M В = T _cp b 1 R ² [ k a ₀ + a r ( 1 - k ) - a 1 - 2 y] . (25)

Поскольку

h - h a0 = A---, ar

R

^h 0 ^- hb  „ _  ^h 1 ^- hb

, «1 =              ,

R ¹ R

то, принимая во внимание выражение (22) имеем

M В = T cp b RRR [ k^h п - h b + ( 1 - k ) V h 0 - h b -

—

V h 1" - hb - 2 Л | ■ ^(1- e 0? ( i + 1 ) hr ^PL v ^R N      h 0 p 0

.

Мощность на бочке валков определяется по известной формуле

N В = M _В ю .                           (27)

При допущении в формуле (26), что материал в процессе деформации не уплотняется (т. е. P 1 = p ₀, h _п = h ₀ , k = 1), а эластическое восстановление отсутствует ( h_b = h 1 ), она преобразуется к виду