Особенности визуализации знаний и информации в курсе математической физики

Математическая физика – это теория математических моделей физических явлений, занимающая особое положение в математике и физике, находясь на стыке этих наук. Данная дисциплина оперирует сложными математическими моделями, абстрактными физическими понятиями и сложными математическими методами, которые изучаются студентами в процессе их подготовки по математике и физике. Однако, как показывает практика преподавания математической физики, студенты не всегда могут точно определить, какие математические методы, физические законы необходимо применить для решения данной задачи, вывода формулы или метода. Таким образом, для эффективного обучения педагогу приходится постоянно возвращаться не только к основам математики и физики, но и к пройденным темам дисциплины с целью формирования единой системы знаний курса, его образного понимания и готовности применять полученные знания на последующих дисциплинах. Прежде чем объяснить новый материал, необходимо сформировать систему базовых знаний, активизировать ту часть ментальных образов, без знаний которых процесс обучения невозможен. Так, например, в курсе математической физики при выводе уравнения равновесия мембраны необходимо сформировать образ мембраны: что такое мембрана, ее характеристики, какими свойствами она обладает и т. д., также необходимо вспомнить некоторые физические понятия и законы (внешняя поперечная нагрузка, равнодействующая сил, закон Ньютона) и активизировать знания математических методов, необходимых для вывода уравнения. Однако в рамках ограниченного числа аудиторных часов и большого объема содержания дисциплины такая форма работы не всегда возможна [Рукосуева, 2008, с. 243]. Такой ход изложения материала связан с высокой абстракцией математики и физики, сложностью математического языка, в котором каждый символ – уже абстракция. Сложность распознавания математического языка, математических и физических моделей ведет к трудностям восприятия информации в целом, и, как следствие, теряется значимость изучаемого.

Эти проблемы актуализируют применение особого способа представления курса математической физики в виде электронной обучающей системы с использованием методов компьютерной визуализации. Применение различных методов визуализации знаний и информации улучшает процесс усвоения информации и стимулирует когнитивные процессы, позволяет повысить эффективность восприятия материала, обработка которого занимает минимум времени. Тщательно подобранные и взаимосвязанные единым подходом теоретический и практический материалы, задачи и задания, дополнительная информация и другие элементы обучающей системы курсу математической физики в совокупности раскрывают содержание дисциплины, укрепляют межпредметные связи и усиливают практическую направленность курса [Tergan, Keller, 2005, с. 5].

В материале дисциплины «Математическая физика» можно выделить основные конструкции, визуализация которых позволяет наиболее полно раскрыть суть курса и дать понимание фундаментальных идей передаваемых знаний и умений – это содержание, текст, функции, формулы, задачи и графики. Каждая конструкция обладает своей спецификой, поэтому может быть представлена разными моделями визуализации. Рассмотрим их подробнее.

Содержание – то, о чем рассказывается; темы, основной смысл, сущности изложения. Содержание должно быть представлено в виде связанных его компонентов, что позволяет сформировать у студентов целостное понимание курса, установить связи не только внутри дисциплины, но и с другими дисциплинами, без знаний которых невозможно успешное обучение. Содержание можно представить с помощью двух моделей: дерева и ментальной карты.

Дерево (tree)

Показывает иерархию набора данных, в которой элементы являются родительскими или дочерними по отношению друг к другу. Дерево выстраивается в виде соединенных линиями узлов, как правило, сверху вниз (рис. 1) [Ветров].

Ф Осмориыо урм*еимя uhhmwhi^ фнхми

Ф Урмнение переноса ф уравнение гепполсоеодеостм ф Урынеиие р*|иц«и* weuOp »*ы ф Уравнение «опебанмяструим ф Урмнения Лапласа и

• методы решения задачи if rum

Ф Рад Тейлор»

• • неопределим»* интеграл Счкчиь- методы интегрирования

• ♦ Определенный интеграл

Ф Двойной шоеграл

• • Задач» Коши для уравнения переноса

гомермэе уоаеняние тепгопр:яодне>сти ф Зад»-» кош* для »рмн*нм< :оппо41рокмбно<1и

Ф нам*%мые * <^twe ywen* Задаче Коши дм фамшиия юля

Ф Kpaeive аад»м щ* уряеиеиия Лаппма

• Решение задх* Кош* для д*»5«-еицийг\^го «-мнения первого л «яд# а

Принцип суперпозиции

• •    Решение тедами Коши дифференциального уре»и»нмя переого nop#

ФМепцФурке                                   • геиенне »р«не-ияк с-«>aw*» оес«свечной струмы • с> ф Метод р«доп»*ня пер4ы«н>>«л    • Рнмнне л иньш* теллопрм-эдности • систем» Maple

Ф Понятнее о стоенш еосхав

Ряды Фгрье

ф Ряды £УРЬ» АЛ*чИяые И WWtTHMl фуМГфН

• •    Комплексная форма ряд» Фурье

Рис. 1. Фрагмент визуализации содержания математической физики в виде дерева

♦ Понятие интеграла Фурье

Ментальная карта (mind map)

Ментальная карта – это удобная и эффективная модель визуализации мышления, представления об объекте или явлении в целом. Ее можно применять для создания и фиксации идей, анализа и упорядочивания информации, принятия решений и т. д. Содержание, визуализированное с помощью ментальной карты, отражает основные темы дисциплины, основные понятия и фундаментальные знания, представленные как модель знаний предметной области курса в виде графа со всевозможными связями отдельных его единиц, так как мысли образуют структуры, которые не являются последовательными, они связаны множеством возможных переходов (рис. 2) [Колесник, 2005].

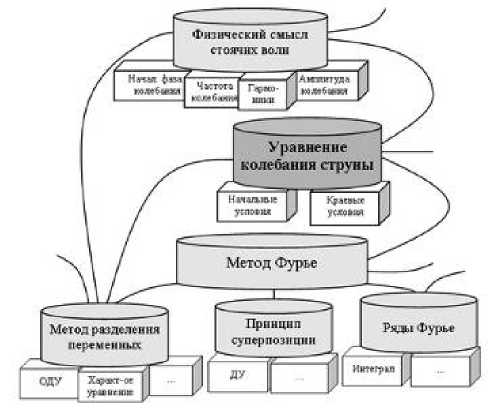
Рис. 2. Фрагмент визуализации содержания математической физики в виде ментальной карты

Текст – любая запечатленная в письменном виде информация, касающаяся конкретной темы изучаемой дисциплины. Тексты, представленные в традиционном виде, обладают некоторыми недостатками. Как правило, это двумерный, линейный текст. Трехмерный звуковой сигнал кодируется в статическое двумерное сообщение, где теряется около 30 % информации. Отражают опыт, тезаурус того, кто написал текст, учат на чужом субъективном опыте. Формируют недеятельностные кодовые образы, а чисто информативные, где теряется еще до 50 % образной деятельностной информации.

Требования к современным электронным текстам вытекают из необходимости ликвидировать эти недостатки, а также приблизить процесс обучения к естественному процессу восприятия мира. Так, подходя к изучению новой дисциплины, каждый студент имеет свой запас знаний, активизация которых позволит более полно понять суть изучаемого.

В качестве визуальной модели представления текста мы предлагаем использовать трехмерный текст, который позволит индивидуализировать содержание материала в зависимости от запаса знаний каждого учащегося.

Трехмерный текст (3D text)

Трехмерный текст – это текст, где каждое понятие (слово, предложение) раскрывается в виде кубика. Понятия раскрываются не на плоскости, а в трехмерном пространстве. Основной текст представлен как бы в двухмерной плоскости, а вспомогательный, разъясняющий основные понятия, размещается по третьей координате. Использование трехмерного текста позволяет не только найти нужную информацию, но и сформировать текст по своему усмотрению, выбирая только те фрагменты, которые студенту кажутся избыточными, уже знакомыми или не представляющими интереса с позиции изучаемой темы, что позволяет ему более осознанно воспринимать сложную информацию [Одноколова, Пак, 2008, с. 191].

Ниже представлен пример трехмерного текста, реализованного с помощью технологии гипертекстового локального сворачивания текста (рис. 3, 4).

Теорема / (Дирихле). Если функция f(x) периодическая с периодом 2я непрерывна или имеет конечное число точек разрьва первого рода на отрезке |-я,я] и этот отрезок можно разбить на конечное число частей, в каждой из которых Дх) монотонна , то ряд Фурье оптосительно функции с ходится к Дх) в точках непрерывное™ и к среднеарифметическому односторонних пределов в точках разрыва первого рода Функция, удовлетворяющая этим условиям, называется кусочно-монотонной.

Рис. 3. Основной текст

Рис. 4. Основной и вспомогательный тексты

Теорема 1 (Дирихле). Если функция Их) пернодтнеская с периодом 2л непрерывна или имеет конечное число точек разрьва первого рода на отрезке [- я,я) и этот отрезок можно разбить на конечное число частей, в каждой из которых Дх) монотонна (<>бщсе название для функций, изменяющихся в одном направлении, то есть для возрастающих, строго возрастающих. убывающих, строго убывающих), то ряд Фурье относительно функции сходится к Дх) в точках непрерьвности и к среднеарифмептческому односторонних пределов в точках разрыва первого рода. Функция, удовлетворяющая этим условиям, называется кусочно-монотонной.

Формулы и функции

Формула – комбинация математических знаков, выражающая какое-либо предложение, правило. Функция – переменная величина, меняющаяся в зависимости от изменения другой величины.

Одна из проблем математических дисциплин – это сложность математического языка, в котором каждый символ является уже обобщением. Данный язык, несмотря на все его достоинства, недоступен части студентов. Громоздкие выводы формул, использование специальных функций и знаков приводит к тому, что студент теряет суть изучаемого процесса или явления, не замечает очевидные факты, а углубляется в математические методы решения, рутинные вычисления и интерпретацию математических знаков. При изложении нового материала преподавателю необходимо указывать на ключевые моменты, комментировать ход решения задачи или вывод формулы. При обучении курсу математической физики с помощью электронной обучающей системы данные проблемы можно решить, используя контекстные подсказки и всплывающие окна [Рукосуева, 2007, с. 140].

Контекстные подсказки (help context)

Контекстные подсказки удобны при кратких комментариях в выводе формул, указании на ключевые моменты материала в словесной форме, являющиеся необходимыми и достаточными для определения используемого метода решения или специальной функции (рис. 5) [Барышкин, Резник, 2005, с. 40].

tsCr + ctij + ^x-ai) 1 г           1 г

2              2й { у 2й ' у

Изменим пределы интегрирования: f/(i)^ =-f Дг)^

= ^^±^^ ₊ ±Т^ Г = ^ + at) + ^-^) ₊ ±Т

2       ^2а {^^J 2а               2         2а *

Рис. 5. Фрагмент вывода формулы Даламбера

Сложим два интеграла ]"Дг№+- [/(г№ = \ ДД<кг.

Всплывающее окно (pop-up)

Математические тексты часто содержат ссылки на ранее выведенные формулы или введенные новые функции, поиск которых замедляет процесс обучения, прерывает ход изучения нового материала. Всплывающие окна используются для отображения информации, скрытой за ссылкой, без изменения материала текущей страницы (рис. 6).

Тригонометрический ряд । I называется тригонометрическим рядом Фурье, а о», ^, Ь, - коэффициентами р дx).91♦2(a„co№x♦^*№c)

2  ч-1   _______ _

Ряд Фурье — способ представления произвольной сложной функции /(х) суммой более простых. В общем случае количество таких функций может

Рис. 6. Всплывающее окно с формулой тригонометрического ряда Фурье

Задача — вопрос, требующий решения на основании определённых знаний и размышлений. Также задача является одним из методов обучения и проверки знаний и практических навыков учащихся, поэтому визуализация как хода решения задачи, так и самого решения очень важна. При введении типовых задач отдельной темы учитель стремится формализовать процесс решения, используя алгоритмы, визуализация которых возможна при использовании блок-схем. Результат задачи можно представить с помощью графиков.

Формализованная блок-схема (block diagram)

Формализованная блок-схема показывает ключевые шаги, которые проходит процесс, в виде связанных друг с другом однонаправленными стрелками блоков. Отображается в стандартизированном формате, где вид блока зависит от его роли в процессе [Ветров]. Ниже представлена блок-схема процесса приведения диффе- ренциального уравнения с частными производными второго порядка к канони- ческому виду (рис. 7).

<*./>« ♦ 2X*./>_V ♦<*.?’>«„ ♦KW»..«,)^eO

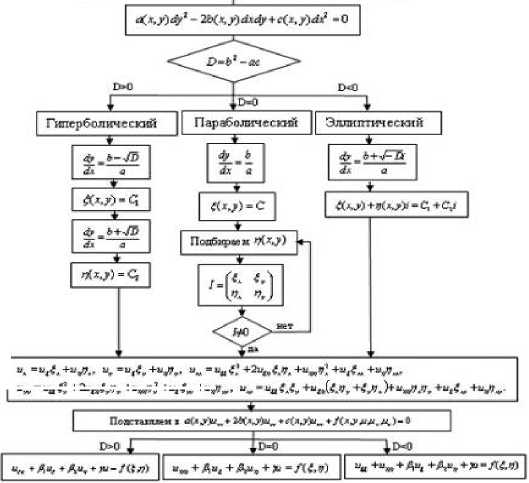
Рис. 7. Приведение дифференциального уравнения с частными производными второго порядка к каноническому виду

График – диаграмма, чертеж, изображающий посредством кривых количественные зависимости различных процессов. График является универсальной моделью визуализации материала математических дисциплин. Так, вывод основных уравнений математической физики невозможно представить без иллюстраций, описывающих изучаемые процессы и явления, специальная функция тяжело воспринимается в математических символах, когда график может разъяснить многое, поиск и анализ решений задач с помощью графиков может облегчить усвоение смысла решаемых задач и представить результаты вычислений в наглядной форме [Рукосуева, 2007, с. 143].

Линейный график (line chart, area chart)

Линейный график объединяет линией набор точек, соответствующих значениям по осям. Такие графики можно построить для функций, зависящих от одной переменной или двух, где вторая переменная является зафиксированной временной характеристикой ( u ( x,t ) , где t - заданное число) (рис. 8) [Ветров].

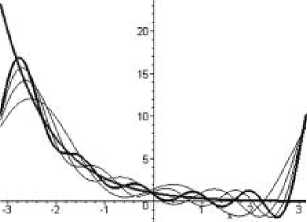
Рис. 8. График функции f ( x, t ) , где t = 1..5

Тепловая диаграмма (heat map)

Сравнивает значения внутри набора данных, закрашивая их одним из цветов в заранее выбранном спектре. Основой является изображение или другая диаграмма, на которой расставлены значения. Цвет зависит от величины параметра и чаще всего накладывается в виде пятен. Например, процесс нагревания пластины [Ветров].

Трехмерный график (3D image)

Трехмерные изображения дают более реалистическую картину, более полное восприятие и формирование образа. Трехмерные графики стоятся для функций, зависящих от двух переменных или трех, где третья переменная является зафик- сированной временной характеристикой рассматриваемого процесса. Примером такого графика может быть визуализация решения задачи Коши для дифферен- циального уравнения с частными производными первого порядка (рис. 9).

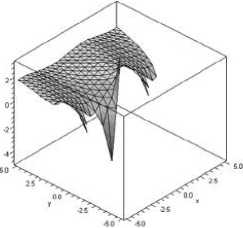
Рис. 9. Решение задачи Коши для уравнения

Рисунок (picture)

Рисунок – изображение, выполненное с помощью графических средств – контурной линии, штриха и т. д. Различными сочетаниями этих средств в рисунке достигается моделирование изучаемого процесса или явления, что облегчает процесс изучения нового материала. Например, для вывода уравнения колебания струны строится рисунок, изображающий элемент струны и силы, действующей на него (рис. 10).

f^

Рис. 10. Колебание струны

Анимированные графики (animation)

Анимация – технология мультимедиа, воспроизведение последовательности картинок, создающее впечатление движущегося изображения. Анимированную графику удобно использовать при рассмотрении процессов и явлений, зависящих от времени, например, колебание струны, колебание мембраны, процесс нагревания стержня, пластины и т. д.

Таким образом, компьютерная визуализация знаний и информации в курсе математической физики представляет одну из основополагающих платформ для эффективного восприятия студентами учебного материала, образного его понимания и применения полученных знаний в дальнейшем процессе обучения.