Особенности выбора представлений полей вспомогательных источников частичных областей

Модель рупорного излучателя

В соответствии с методом частичных областей [1] полагаем, что каждая частичная область электромагнитно изолирована, сторонние источники в областях отсутствуют, а возбуждение областей осуществляется эквивалентными токами, распределенными на поверхностях, ограничивающих области. Накладываем на тангенциальные компоненты электрического поля вспомогательного источника условие равенства нулю на поверхности, ограничивающей область. Тогда по- ле в частичной области возбуждается эквивалентным магнитным током. Поскольку на идеально проводящих участках поверхности, ограничивающей область, касательная составляющая вектора

E равна нулю, эквивалентные магнитные токи, пропорциональные E , отличны от нуля только на неметаллизированных участках поверхности:

bH ( P ) = J j" ( q ) Н м ( P , q ) dS q .                        ₍₁₎

S

Здесь Н м ( p , q ) — возбуждаемые в точке p векторы напряженности магнитного поля вспомогательного магнитного источника (пропорциональные функции Грина данной области), расположенного в точке q, находящейся на поверхности, ограничивающей область; j^M ( q ) - эквивалентный магнитный поверхностный ток.

j^M = [ n , E ( q ) ] ,                                          ⁽²⁾

где n - внешняя нормаль к поверхности S, ограничивающей область; E(q) - вектор напряжен- ности электрического поля в точке q; b - единичный вектор, вдоль которого ориентирован вспомогательный магнитный диполь.

Полагаем, что излучатель возбуждается волнами типа Т, набегающими по волноводу (область V0) из минусбесконечности. В связи с этим в системе существуют только следующие составляющие электромагнитного поля: Н х , Е у , Е z .

Для примера запишем представление для составляющей Н х магнитного поля в области V1. Принимая во внимание совпадение смежных поверхностей S 3 , и S 6 , S 4 , и S 8 , S 2 , и S 10 , а также совпадение неметаллизированного участка поверхности S 1 с S 0, , имеем в точке наблюдения ( Р , 1 ) частичной области V1:

^Нх, , ( P v 1 ) = J ^E „ 0 ( q . ) H " 1 ( p , 1 . 4 s 0 ) dS 0 -

S 0

- J E , 1 ( q S 2 H " 1 ( p , 1 , q s 2 ) dS 2 -

S 2

- J E , 3 ( q_s 6 ) H " 1 ( p , 1 , q 6 ) dS 6 +

S 6

^{+ J E} z , 4 ⁽ q^S 8 ) ^HXV 1 ^{( P v} 1 . q^S 8 ) ^dS 8 .                             (3)

S ₈

Здесь E , E , E , E - тангенциальные составляющие электрического поля об- y ^{V 0}      y^V 1      z , 3      z v 4

ластей V0,V1,V3 и V4 в точках qS qS , qS UqS  поверхностей S0, S2, S6 и Ss, ограничи- вающих область V1.

Учитывая, что каждую поверхность можно рассматривать как плоскость, перпендикулярную продольной оси волновода (направленного по осям y либо z ), составляющие электрического поля целесообразно представлять в виде поперечных компонент электрического поля соответственно ориентированного волновода [1, 2].

Аналогичным образом можно представить поля в областях V2, V3 и V4.

Поле в области V0 представлялось в виде разложения по системе волноводных гармоник.

Для обеспечения единственности решения электродинамической задачи необходимо приравнять тангенциальные составляющие магнитного поля смежных областей на границах их раздела, т.е. совместить точки наблюдения на границах раздела смежных областей. В результате получим систему интегральных уравнений, которая в операторном виде представлена следующим образом:

<

H 2 (y‘, z ' = 0) = HXy 1 (y‘, z ' =0

HXy 2 (y ’, z ' = 0) = HXy з (y', z ' =0

HXy 2 (y', z ' = 0) = Hxy 4 (y', z ' =

H x y i ( У ' = Ь з , z ' ) = H x y з ( У ' = Ь з , z '),

H x y i ( У ' = Ь з + b i , z ' ) = H x y 4 ( У ' = b з + b i , z '), H x y i ( y', z - = d d ) = H x y 0 ( У', z ' = - d ),

где штрихованные y' и z' обозначают координаты точек наблюдения.

Таким образом, приравниваются как тангенциальные магнитные, так и тангенциальные электрические компоненты полей смежных областей.

Решение системы интегральных уравнений выполнялось методом Галеркина.

Для конкретизации представления полей Н М ( Рq ) в частичных областях необходимо

решить задачу о возбуждении соответствующей частичной области бесконечной нитью магнитного стороннего тока, ориентированной вдоль оси Oх и имеющей единичную амплитуду и нулевую фазу. Решение производится в два этапа.

На первом этапе решается задача о возбуждении плоского волновода. Решение неоднородных уравнений Максвелла сводится к решению неоднородного уравнения Гельмгольца для комплексных амплитуд магнитного векторного потенциала А ^M [2]. Вектор напряженности магнитного поля выражается через векторный потенциал. Решение уравнения Гельмгольца представлялось в виде разложения в ряд Фурье для волны, бегущей в направлении оси z (первый волновод) и оси y (второй волновод):

1 ж\

A M ⁽ У’ ^z ) = Г 2 ^e p Yip ^{cos (} Р^{п b} i - У ) ^{cos (} Р^п b i - ¹ У ') ^exP [± Y i р ^{( z} - ^z ')] , b i Р = 0

Здесь:

A M ( У , z ) = ¹ x ГВ           _d

”

2 ^ р Т 1 Г p ^{cos (} p n d ¹ z ^{)cos (} p n d ¹ z ^,)ex p [± Y i r_p ⁽ y - y ') ]

р = 0

γ 1 Г

—

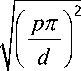
^ i ;

ε

γ 1 p

pπ

N I b i )

—

E i ;

при при

р = 0 р ф 0 .

Нештрихованные у и z соответствуют координатам источников.

На втором этапе к полученному выше решению неоднородного уравнения добавляется решение однородного уравнения Гельмгольца. Это решение для каждой парциальной волны содержит два неизвестных коэффициента :

АМмодн =чг2£рУ11 (Е1 Ре"Y1 рz+E2PeYр2)cos(рпbi—1 у)cos(рпbi—1 у');(7)

^{2 b} 1 р = 0

1 ”

АМодн =412ерY1Гр(Е3Ре Y1 ГрУ + E4peYГрУ)cos-(Pnd 1 z)cos-(Pnd 1 z') .(8)

2 d р = 0

Неизвестные коэффициенты Е определяются из граничных условий для тангенциальных составляющих напряженности электрического поля на торцевых стенках резонатора. В результате получим следующие выражения для магнитного поля вспомогательного источника резонатора

(областьV1), образованного из волновода, в котором распространяется волна в направлении оси z или y (резонатор с продольным направлением по оси z или у ):

Н^м x V 1

1 ”       £

= - «^i—L---p— bl p=0 Y1 psh(Y1 pd)

pn ( , ,X cos ^(y - b3) cos b

f ( y - b 3 ) x . ^b 1              ]

ch⁽Y i p z ) ch ^[ / i p ⁽ d + z ') ] ^пР^и z ' <  z

XS

ch ⁽Y i p z ') ch ^[ / i р ⁽ d + z ) ] при z' >  z ;

Н^м x V 1

=- L  £p 11) p d p=0 Yi rpsh(Y1 rpbi)

pn ,     pn cos ^—z cos ^—z x

d

рπ

d

ch ⁽Y i Г Р ( y ^{- b} 3 )) ch ^[ Y i Г Р ( y '- b ^{- b} i ) ] при y’ >  y

xS ch(YiГР(y’ - b3)) ch [YiГР(y - b3 - bi)] пРи y’ < y.

Таким образом, соотношения для полей вспомогательных источников могут быть представлены различными выражениями.

Выбор выражения для поля вспомогательного источника целесообразно увязывать с видом представления эквивалентного тока, распределённого на конкретной поверхности, охватывающей область. Рассмотрев два варианта представления полей вспомогательных источников, установили, что более предпочтительным является такое представление поля вспомогательного источника, которое характерно для резонатора с продольным направлением, совпадающим с продольным направлением волновода, через поперечные составляющие электрического поля которого выражается эквивалентный поверхностный ток, входящий в подынтегральные выражения.

Проведем вывод коэффициентов, описывающих связь гармоник поверхностного тока на S0, c гармониками поверхностного тока, распределенными на поверхности S3, при сшивании полей областей V0 и V1 по границе раздела S0. Эта группа коэффициентов вычисляется после соответствующих преобразований третьего слагаемого правой части выражения (3). При применении метода Галеркина в качестве весовых функций использованы базисные функции разложения по- верхностных токов на поверхности S0: соs

m0nr„-                                              „

“T^- ( ^{y - y} i ) , базисные функции на поверхности 5 3 . ^b 0              ]

имеют вид соs

m 3 Г π

где m 3 Г - номера гармоник волновода, ориентированного вдоль

оси у, а m о - номер весовой гармоники. В соответствии с методом Галеркина после умножения интегрального уравнения, определяющего связь поля возбуждающего волновода (область V0) с полем в области V1 (см. шестое уравнение системы (4)) на весовые функции, производится интегрирование по точкам наблюдения.

В первом случае при выводе коэффициентов используем выражение для поля вспомогательного источника резонатора с продольным направлением по оси z . Точки наблюдения при этом имеют координаты у ’, Z= - d, точки источников - y = ( b 3 , z ) . Подставляем выражения для электрического поля и поля вспомогательного источника при условии, что z′. В результате получим следующее выражение:

yi +b о      Г г                  По 1 от                  /\

‘                m п                  i                  । m ^ р П ।

Ci0Lm03г = f cos       (y - yi) f (- — )L Y3Гт3Г cos I -^pz Iх yi       L bо             ]- d    l£3 m 3 гX

p^- ( y '- ^b 3 ) ^ch ( Y i p ^z ) ^dzdy '. b i

/ ■ x i

x(-i£i)— L ------ bi p=0 Yipsh (Yipd)

После вычисления интегралов получим:

С 10 L^{m ' 0} m _{3 Г}

εγ

3 Г _{m 3 Г} ε ₃ b ₁

to             о

( - 1 ) ^m 3 г У--------- f F 1 , ^ = 0 2 f m з r ⁿ |

Y1 p A d J

где

F 1 = ^

ра с этом

pπ

b1

^m 0 ^П I ^pn I

I - I к b 0 ) к ^b 1 )

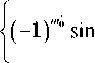
П ( Ь з - > 1 - b 0 ) b ₁

- Sin

f^{( b} 3 - > 1 )

pn  m П при ,   ' o-5L_,

b1     b0

b

⁰ cos

b0

f⁽ b 3 - > 1 )

pπ

при b1

= m0n * 0, b0       ,

pn m П - при ²— = —— = 0 .

b1     b0

Во втором случае используем выражение для поля вспомогательного источника резонато-

продольным направлением случае запишется:

по оси у . Исходное выражение для коэффициента С 10 L^m m ⁰ _{3 Г} в

С 10 L^m m ⁰ _{3 Г}

> 1 ^{+ b} 0

J cos y1

m '₀ π b ₀

1  0 (

( > ' - > 1 ) x J

_ — d к

i ε

к

to

У Y3rm3Г cos

-3 ) ^m 3 Г = ⁰

m, n 1

—³²— z x d )

о p ( - 1 ) ^p

to

x(-io1)1У      / X dp^0 Y1 rpsh ( Y1 rPb1)

cos ^ p ⁿ z Jx ch [ / 1 _pr ( > '- b ₃ - b 1 ) ] dzdy '.

После интегрирования:

c 10 п^0 = m3 Г

ε

γ 3 Гm 3 Г

ε m _{3 Г}

m ' ₀

где

F 1 = ! 1

ε m 3 Г

γ _{3 Г}

ε ₃

s^{h (} Y 1 Гт 3 г^Ь 1 )_л 2

γ 1 Гm

3 Г

+

^{2 m} ° ⁿ к ^b 0 )

1 ^{m 3 Г} x

s^h [ / 1 Гт з г ( > 1 ^{+ b} 0 - ^b 3 - ^b 1 ) ] - s^{h [} Y 1 Гт 3 r ( > 1

_ '1

при

при

при

m 3 г = 0 ;

m ₃ Г ^ 0 ;

при

m 3 Г π

\ к d

b ₃

m 3 г = 0 ;

m _{3 Г} ^ 0 ;

- £3 •

)

Аналитические выражения для вычисления коэффициента С 10 L^m_m ⁰ различны. Соотношение (12) включает в себя суммирование в бесконечном пределе по индексу р , в то время как соотношение (14) позволяет вычислять значение коэффициентов непосредственно. Однако численные значения коэффициентов, вычисленные по соотношению (12), при увеличении числа членов суммирования по индексу р стремятся к численному значению коэффициентов, вычисленных по (14).

В таблице приведены значения коэффициентов С 10 L m ; при различных т 0 и m 3 г , вычисленные по соотношению (12) при учёте разного количества слагаемых ряда по р . В последней справа колонке таблицы приведены значения коэффициентов, рассчитанные по соотношению (14). Расчеты проводились при следующих параметрах излучающей системы (см.рисунок): Ь о =О,ЗО п , Ь 1 = Ь з = Ь 4 =0,23 п , d =0.8 n , £ 0 =1, £ 1 =3, £ 2 =1, £ з = £ 4 =3, У 1 = 0.195 п .

Значения коэффициентов С 10 L m3_r

P	10	50	100	150	500	С 10 Lm ' 0 m 3 Г
z-ч т '0 = 0 m 3 г = 0	0,00000000 -0,538781237j	0,00000000 -0,539275190j	0,00000000 -0,539281207j	0,00000000 -0,539281753j	0,00000000 -0,539281752j	0,00000000 -0,539281752j
т '0 = 0 Ст з г = 2	0,233486849+ +0,00000000j	0,232470465+ +0,00000000j	0,232457916+ +0,00000000j	0,232456777+ +0,00000000j	0,232456780+ +0,00000000j	0,232456780+ +0,00000000j
m '0 = 1 Ст 3 Г = 0	0,00000000+ +0,236506601	0,00000000+ +0,236143398j	0,00000000+ +0,236137785j	0,00000000+ +0,236137316j	0,00000000+ +0,236137353j	0,00000000+ +0,236137353j
С т '0 = 1 т 3 Г = 2	0,129104918+ +0,00000000j	0,1283556224+ +0,00000000j	0,128344520+ +0,00000000j	0,128343542+ +0,00000000j	0,128343619+ +0,00000000j	0,128343619+ +0,00000000j

Как следует из таблицы, при увеличении числа членов ряда по р в выражении (12) значения коэффициента С 10 L^m m ₃ ⁰ _Г стремятся к значениям, вычисленным по выражению (14). Для выбранных размеров излучающей системы совпадение значений коэффициентов в пятом знаке после запятой имеет место при р >100. При увеличении размера b 1 совпадение значений с заданной точностью наступает при учёте меньшего количества слагаемых в выражении (12).

Выводы. Результаты вычисления подобных элементов блочной матрицы показали, что численные значения коэффициентов, рассчитанные по соотношениям (12) и (14), совпадают. При этом совершенно очевидно снижение вычислительных затрат в случае использования поля вспомогательного источника резонатора с продольным направлением, совпадающим с продольным направлением волновода, по поперечному размеру которого производится интегрирование. Это обусловлено тем, что хотя соотношения для расчета коэффициентов имеют один порядок сложности, но в одном случае (см. формулу (14)) вычисления производятся один раз, а в другом случае (см. формулу (12)) – сотни раз.