Особенности вычисления корней уравнения Матье в системе Maple

При решении уравнений Гельмгольца для изотропных и гиротропных эллиптических волноводов соответствующие дисперсионные уравнения выражаются через функции Матье [1]. Следовательно, при решении дисперсионных уравнений приходится вычислять корни уравнения Матье, чаще всего с использованием системы компьютерной математики Maple [2]. При этом приходится сталкиваться со следующими особенностями вычисления корней уравнения Матье в системе Maple:

• 1.    При численном вычислении корней в Maple используется специальная команда fsolve , которая не позволяет для функций Матье получить все существующие на указываемом интервале корни.

• 2.    Для нахождения всех корней функции Матье на заданном интервале требуется анализ работы команды fsolve, на что затрачиваются дополнительные временные и умственные ресурсы.

Целью данной работы является устранение отмеченных выше недостатков вычисления всех корней функции Матье на заданном интервале путем разработки алгоритма и подготовки соответствующей программы — надстройки над существующими функциями в системе Maple, которые позволят контролировать интервал поиска корней с гарантией исключения пропуска корней.

1    Функции Матье в системе Maple

Решая задачу об эллиптической мембране, Матье получил дифференциальное уравнение следующего вида [1]:

О y

—2 + ( a - 2 q cos2 z ) y = 0.                   (1)

5 z

В задачах об эллиптической мембране решения уравнения (1) называются обыкновенными функциями Матье. Они имеют период п или 2п относительно z. Условие периодичности решения этого уравнения определяет ряд значений a в зависимости от q (называемых собственными значениями). Если q = 0, то а = n2(n = 1,2,...) и функции Матье совпадают с тригонометрическими функциями cos nz и sin nz . При q # 0 функции Матье, обозначаемые cen (z, q) и sen (z, q), представляются в виде [3]:

да

ce_n ( z , q ) = E aV cos(2 k + г ) z , k = 0

В системе Maple для вычисления корней обыкновенных функций Матье, являющихся периодическими решениями уравнения Матье (1), доступны функции MathieuCE и MathieuSE для четной и нечетной периодических функций Матье соответственно.

2    Алгоритм вычисления корней Матье в системе Maple

Для численного вычисления корней в Maple предусмотрена команда fsolve() , которая позволяет найти корни уравнения или системы уравнений в численном виде. Синтаксис вызова функций для вычисления корней Матье в численном виде, идентичен для обеих функций и выглядит следующим образом¹:

fsolve ({ MathieuCE ( n , q , z )}, { z }, { z = 0 ..2 Pi });            (4)

fsolve ({ MathieuSE ( n , q , z )}, { z }, { z = 0 .. 2 Pi });            (5)

В данном примере приведено именование аргументов функций, отличное от используемых в официальной документации Maple², но в таком виде оно в большей мере отражает взаимосвязь канонической формы уравнения (1) и аргументов функции в Maple. Отметим, что интервал поиска корней указан от 0 до 2 п , что прямым образом вытекает из условия периодичности решения уравнения (1). В то же время форма записи (4) и (5) не позволяет выполнить поиск всех корней, которые имеются на указываемом интервале. Это связано с тем, что команда fsolve для трансцендентных уравнений выводит только один корень³.

Так как выводимый корень только один, анализируя работу команд (4) и (5) с различными параметрами, можно ошибочно заключить, что возвращаемые командой fsolve значения корней имеют какой-то тренд, смысл которого заключается в следующем: каждый из найденных корней оказывается ближе к какой-либо из границ интервала или к его центральной части (в зависимости от параметров, при которых проводится поиск). Поэтому в зависимости от характера тренда разработка алгоритма вычисления корней может быть связана с природой, определяемой этим трендом.

Если тренд, при котором каждый вычисляемый корень является последним на заданном интервале, то достаточно было бы предложить алгоритм сужения интервала поиска с конца, как это показано на рис. 1. Отметим, что указанный тренд, заложенный в основу команды fsolve , является основным недостатком этого алгоритма и не позволяет вычислить все корни на заданном интервале, что будет показано ниже по результатам численного эксперимента.

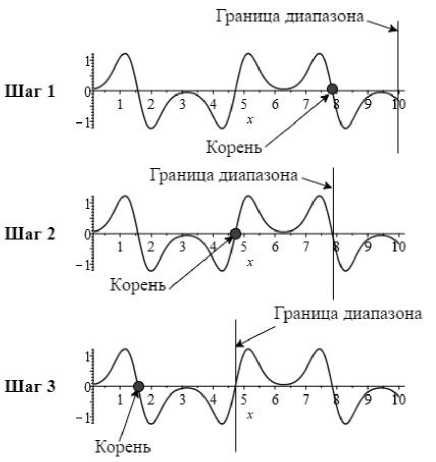
Рис. 1. Схема работы алгоритма А: сужения интервала поиска корней с конца

Алгоритм А вычисления корня по рис. 1:

• 1)    из предпосылки, что определяемый корень является последним, на заданном интервале вычисляется первый корень;

• 2)    верхняя граница интервала сдвигается на позицию того корня, который был найден, и вычисление производится исходя из новых границ поиска, не включая значение новой верхней границы;

• 3)    по аналогии со вторым шагом сдвигается граница поиска с учетом найденного на втором шаге корня и выполняется новый поиск и т. д.

Таким образом, алгоритм А сводится к тому, чтобы вызывать функцию поиска корней каждый раз на новом интервале в предположении о том, что вновь найденный корень является последним.

Альтернативой алгоритму А может служить алгоритм Б, в котором весь интервал поиска корней проходится с определенным шагом с начала интервала. При этом на каждом подынтервале последовательно проверяется наличие корней, как показано на рис. 2.

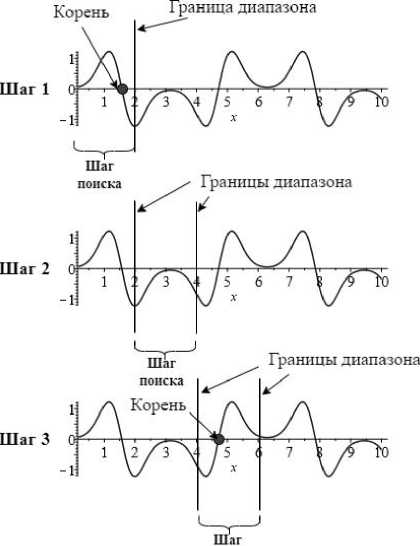
поиска

Рис. 2. Схема работы алгоритма Б: поиска корней с полным перебором

Алгоритм Б вычисления корня по рис. 2:

• 1)    выполняется поиск на интервале между нижней и верхней границами, верхняя граница представляет собой нижнюю границу плюс шаг поиска. Если поиск успешный, корень сохраняется;

• 2)    перенос границы поиска корней: нижняя граница принимает значение верхней границы из шага 1, а верхняя становится больше новой нижней на шаг поиска;

• 3)    по аналогии с предыдущими шагами границы поиска сдвигаются по возрастанию, не зависимо от того, есть корни на конкретном отрезке или нет. При этом значение нижней границы не включается в диапазон поиска.

В работе алгоритма Б большое значение имеет шаг поиска корней и встает вопрос о выборе оптимального шага, и это является основным недостатком.

Отметим, что при экспериментальной реализации обоих алгоритмов учитывался случай, когда корень оказывается на нижней или верхней границе поиска. Поэтому для исключения повторов при указании интервале поиска вводится коэффициент сужения границы, равный 10 ^{- 6}. Для алгоритма А сужения производится по верхней границе, т. е. по значениям найденных корней. Для алгоритма Б сужение выполняется по нижней границе поиска, за исключением первого шага. Сравнение результатов работы обоих алгоритмов, реализованных в Maple, приводится в таблице 1.

Таблица 1

Результаты вычислений c использованием алгоритмов А и Б

Параметры	Периодическая функция Матье: порядок 1, q = 1, интервал поиска от 0 до 4 п
	Четная		Нечетная
Алгоритм	А	Б	А	Б
Найденные корни	1.570796327 4.712388980	1.570796327 4.712388980 7.853981634 10.995574290	0.000000000 3.141592654 6.283185307	0.000000000 3.141592654 6.283185307 9.424777961 12.566370610

Из таблицы 1 видно, что количество вычисленных корней по алгоритмам А и Б различно в результате пропуска корней по алгоритму А.

Краткие результаты экспериментальных вычислений таковы: а) алгоритм А в принципе не применим; б) алгоритм Б за счет большого числа вызовов функции поиска корней ( n = z / s , где z — диапазон поиска, s — шаг) занимает много времени. Очевидно, что добиться сокращения времени работы программы, разработанной по алгоритму Б, можно за счет снижения нерезультативных вызовов функции поиска корней. Лучшим показателем является количество вызовов функции, равное реальному количеству корней на указанном интервале. При этом должна обеспечиваться достоверность отсутствия пропущенных корней.

Отметим, что алгоритм Б пока также не применим из-за трудности определения оптимального шага.

Альтернативой алгоритмам А и Б является алгоритм В. Схема работы этого алгоритма показана на рис. 3. Алгоритм В базируется на модернизации принципа, на котором базировался алгоритм А, с дополнительной проверкой пропущенных корней.

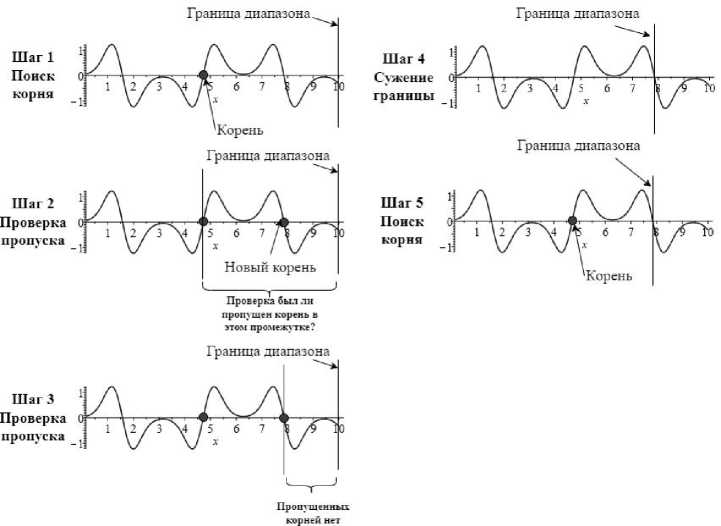
Рис. 3. Схема работы рекурсивного алгоритма В вычисления корней

В алгоритме В на рис. 3:

• 1)    поиск первого корня на всем интервале. Принцип поиска такой же, как на шаге 1 алгоритма А, но без предпосылки, что это будет последний корень, поскольку функция fsolve этого не гарантирует;

• 2)    проверка на пропуск корней. Так как между первым найденным корнем и верхней границей интервала могут быть еще корни, которые функция fsolve не вывела в силу особенностей ее работы. Для проверки пропуска, как в шаге 1, выполняется поиск корней в границах между найденным кор -нем и верхней границей исходного интервала. Если в результате поиска не будет найден новый корень, то найденный на шаге 1 корень считается последним на исходном интервале, иначе осуществляется переход к шагу 3;

• 3)    повторная проверка на пропуск корней. Если по результатам проверки на шаге 2 будет найден корень, тогда снова необходимо убедиться в том, что между новым найденным корнем и верхней границей исходного интервала нет пропущенных корней, т. е. еще раз проводится повторная проверка. Проверка повторяется до тех пор, пока не найдется отрезок между вновь найденным корнем и верхней границей интервала поиска, не содержащий корни;

• 4)    последний корень, найденный на шаге 3, будет последним и для всего интервала поиска, который был задан на шаге 1. Найденный корень сохраняется, а интервал поиска сужается, т. е. верхней границей становится значение этого корня.

Таким образом, для определения всех корней на исходном интервале требуются повторные вычисления по алгоритму В, до тех пор, пока не будут найдены все корни. Алгоритм В имеет рекурсивный характер алгоритмизации и обеспечивает достоверный результат с минимальными временными затратами, что установлено экспериментальными вычислениями.

3    Программа вычисления корней функций Матье в системе Maple

Ниже приводится листинг программного кода, который реализует описанный в предыдущем разделе алгоритм В численного вычисления корней функции Матье. В качестве входных параметров, которые могут изменять режим работы программы, выступают переменные:

• n , q — аргументы функции Матье;

down , up — границы диапазона поиска.

Листинг — Программа вычисления корней функций Матье restart:

• n := 1;

q := 10;

down := 0; #нижняя граница up := 2Pi; #верхняя граница correct := 1E-6; #коэффициент для сужения поиска корней count := 0; #количество корней down_buf := 0;

flag := 0;

a[count] := up+0.1;

for i from 0 to 10000

do if not(type(fsolve({MathieuCE(n, q, z)}, {z}, {z = down .. (a[count]-correct)}), function)) then if (i = 0) then down2 := rhs(fsolve({MathieuCE(n, q, z)}, {z}, {z = down .. (a[count]-correct)})[1])+correct;

up2 := a[count];

else if (flag = 0) then down2 := rhs(fsolve({MathieuCE(n, q, z)}, {z}, {z = down .. (a[count]-correct)})[1]);

else end if;

up2 := a[count];

end if ;

if not (type({fsolve({MathieuCE(n, q, z)}, {z}, {z = (down2+correct) ..

(up2-correct)})), function)) then flag := 1;

down_buf := rhs(fsolve({MathieuCE(n, q, z)},  {z}, {z =

(down2+correct).. (up2-correct)})[1]);

down2 := down_buf;

next;

else if(flag = 1) then flag := 0;

down_buf := 0;

count := count+1;

a[count] := down2;

down2 := 0

else count := count+1;

a[count] := rhs(fsolve({MathieuCE(n, q, z)}, {z}, {z = down ..

(a [count-1]-correct)})[1]);

end if;

end if ;

else break;

end if ;

end do ;

for i from 0 to (count-1)

do printf("%10.9f \n", a[count-i]);

end do ;

Результатом работы программы являются выводимые в главном окне программы значения корней функции Матье.

4    Анализ результатов работы программы

В таблице 2 приведены результаты вычисления корней четной и нечетной функций Матье при различных параметрах в интервале [0;2я]. В [4] приведены значения корней четной и нечетной функций Матье в ин-π тервале [0;—]. Их сравнение с аналогичными корнями из таблицы 2 для

π интервала [0;— ] показывает полное совпадение.

Таблица 2

Результаты вычисления с использованием алгоритма В

Порядок	Четная функция (CE)		Нечетная функция (SE)
n	q = 1	q = 10	q = 1	q = 10
0	–	–	–	–
1	1.570796327	1.570796327	0.000000000	0.000000000
	4.712388980	4.712388980	3.141592654	3.141592654
			6.283185307	6.283185307
2	0.938516101	1.269885505	0.000000000	0.000000000
	2.203076552	1.871707148	1.570796327	1.570796327
	4.080108755	4.411478159	3.141592654	3.141592654
	5.344669206	5.013299802	4.712388980	4.712388980
			6.283185307	6.283185307
3	0.583350428	1.017368826	0.000000000	0.000000000
	1.570796327	1.570796327	1.095728202	1.271383072
	2.558242226	2.124223828	2.045864452	1.870209582
	3.724943081	4.158961479	3.141592654	3.141592654
	4.712388980	4.712388980	4.237320855	4.412975726
	5.699834880	5.265816482	5.187457106	5.011802235
			6.283185307	6.283185307
4	0.417971992	0.759271926	0.000000000	0.000000000
	1.200175985	1.324850974	0.818577798	1.034281683
	1.941416669	1.816741680	1.570796327	1.570796327
	2.723620661	2.382320727	2.323014855	2.107310970
	3.559564646	3.900864580	3.141592654	3.141592654
	4.341768638	4.466443627	3.960170452	4.175874337
	5.083009322	4.958334334	4.712388980	4.712388980
	5.865213315	5.523913381	5.464607509	5.248903624
			6.283185307	6.283185307
5	0.326992806	0.520292319	0.000000000	0.000000000
	0.961929185	1.104181369	0.648458145	0.830440515
	1.570796327	1.570796327	1.268347923	1.340420780
	2.179663468	2.037411285	1.873244731	1.801171874
	2.814599848	2.621300335	2.493134509	2.311152139
	3.468585459	3.661884973	3.141592654	3.141592654
	4.103521839	4.245774023	3.790050799	3.972033168
	4.712388980	4.712388980	4.409940577	4.482013433
	5.321256122	5.179003938	5.014837384	4.942764528
	5.956192501	5.762892988	5.634727162	5.452744792
			6.283185307	6.283185307

Как уже отмечалось, приведенные в таблице 2 значения корней функций Матье вычислены только до 2 π . Для того чтобы продолжить таблицу 2 с теми же параметрами, с которыми проведены вычисления, исходя из условия периодичности функции можно воспользоваться формулой:

Ri = 2 п * k + M [ i - k * C ],                      (6)

где Ri — значение i -го корня; k = i divC — целочисленное деление i на C ; i — номер корня £ [0;2 п ) ; C — количество корней в диапазоне [0;2 п ) ; M — множество корней диапазона [0;2 п ) ; M [ n ] — значение n -го корня из множества M .

Заключение

В работе проанализированы особенности вычислений корней функции Матье в системе Maple и выявлены имеющиеся недостатки, касающиеся вычисления всех корней на заданном интервале. Также показано, что даже при наличии достаточно хорошо работающего программного продукта необходимость программирования в системах компьютерной математики не теряет своей актуальности. Приведенные в таблице 2 численные значения корней функции Матье могут быть полезны при отладке программных продукций, реализуемых на языках программирования, в которых нет встроенных команд вычисления корней функции Матье.

В работе предложены законченный алгоритм вычисления всех корней функции Матье на произвольно заданном интервале и его программная реализация. Проведено тестирование путем сравнения результатов вычислений по рекурсивному алгоритму В с соответствующими данными из [4, 5], которое показало корректность алгоритма. Отметим, что представленная программная реализация алгоритма В может быть адаптирована к поиску всех корней на заданном интервале и для других уравнений, в том числе не имеющих периодических решений, что делает ее универсальной при вычислении корней уравнений, содержащих трансцендентные функции и требующих решения в численном виде в системе Maple.

Представленный программный код может быть внедрен в новые проекты в системе Maple, в которых есть необходимость вычисления всей корней функции Матье и ее производных на произвольно заданном интервале в процессе решения многих прикладных задач.

Основные выводы таковы:

• 1.    Установлены особенности численного вычисления корней функции Матье в системе Maple и отмечены их недостатки.

• 2.    Разработаны алгоритм и соответствующий программный код, устраняющий имеющиеся недостатки.

• 3.    Предложенный программный код может быть внедрен в новые проекты системы Maple.