Особенности засветки бленды солнечным излучением, отраженным от поверхности земли

Космические аппараты (KA), функционирующие на орбите Земли, для определения ориентации обычно включают в свой состав звездные датчики. Основными факторами, снижающими эффективность работы звездных датчиков, являются прямое солнечное излучение и солнечное излучение, отраженное от поверхности Земли. Последний фактор особенно значим для КА на низких орбитах.

Для защиты от боковых помех звездные датчики снабжаются блендами. Одним из основных параметров бленды является кратность ослабления светового потока, понимаемая как отношение освещенности от боковой помехи на входе бленды к ее освещенности на выходе в области размещения первой линзы [1]. Ее оценка проводится как экспериментальным, так и расчетным путем.

При проведении испытаний бленд на помехозащищенность от боковых излучений используются имитаторы астрономических источников излучений, обеспечивающие воспроизведение их геометрических и светотехнических параметров [2,3]. Для оценки влияния прямых лучей Солнца используются имитаторы солнечного света, базирующиеся на источниках в виде параллельного пучка световых квантов. Особенностью засветки оптики отраженным солнечным излучением является расходящийся поток частиц на входе защитной бленды, обусловленный геометрической расходимостью отраженного излучения, формируемого поверхностью Земли. Исходя из указанной особенности, имитаторам Земли требуется настройка конструкции прибора на конкретные параметры орбиты, что затрудняет применение их на практике.

Сложности экспериментального определения коэффициентов ослабления бленды обусловили широкое развитие расчетного подхода к их оценке. Для расчета источников боковых помех в виде параллельного пучка часто используются либо приближенные методы [1], либо пакеты прикладных программ по расчету оптических систем, например, ТгасеРго, либо самостоятельные разработки исследователей [4,5]. Для оценок от расходящегося пучка частиц требуются специальные модули, учитывающие расходимость источника излучений.

Настоящая работа посвящена расчетным исследованиям особенностей формирования светового потока отраженным солнечным излучением на выходе бленды по месту размещения первой линзы для КА, функционирующих на орбитах Земли различной высоты, а также их сопоставлению с полями светового потока для боковой засветки от параллельных пучков частиц. Исследования проводились на основе модели, описывающей формирование боковых помех от солнечного излучения, отраженного от поверхности Земли, на входе бленды. Указанная модель была реализована в рамках программы метода Монте-Карло POKC-RG [6], предназначенной для решения уравнения переноса оптического излучения в трехмерной геометрии.

2.    Особенности математической модели

Математический аппарат, описывающий поля оптических излучений от Земли, формирующихся под влиянием Солнца, к настоящему времени достаточно хорошо развит в связи с необходимостью их учета при оценке внешних тепловых нагрузок на КА (см., например, [7-11]).

Основное допущение указанных моделей заключается в том, что поверхность Земли отражает свет диффузно и равномерно во всех направлениях. В реальности коэффициент отражения значительно различается по всему земному шару: он обычно выше в областях, покрытых льдом и снегом, в пустынях и облачных районах и, как правило, ниже в океанах при отсутствии облаков, т.е. зависит от места и времени. Но для простоты он моделируется так, как если бы он был равномерным. Используя рекомендации работы [12], позволяющие учесть наклон орбиты (примем наклон орбиты более 60°), среднее значение коэффициента отражения выбираем равным 0.273.

Исходя из принятого приближения источник излучения в математической модели формируется путем интегрирования отраженного излучения по всей поверхности планеты, попадающей в конус, центр которого находится на КА, а образующие являются касательными к поверхности Земли (см. рис. 1). Величина угла ymax, определяющая указанный конус, равна

7max = arccos(

R

R + H

),

где R - радиус Земли, H - высота орбиты.

Особенности алгоритмической реализации модели методом Монте-Карло состоят в следующем. Исходными данными являются параметры вышеупомянутого конуса: направляющие косинусы оси конуса, соединяющей центр Земли и начало системы координат, связанной с КА, а также угол полураствора вышеупомянутого конуса. Начальное направление моделируемой частицы определяется в несколько этапов. На первом этапе равномерно в интервале (1 — cos(ymax)) разыгрывается угол у, характеризующий кольцевой слой на поверхности Земли, с которого происходит облучение КА. В силу азимутальной симметрии конуса точка на поверхности, с которой происходит облучение КА, разыгрывается в кольцевом слое равномерно по азимуту. Для полученной точки Р определяется угол между направлениями от центра КА к центру Земли и от центра КА к выбранной точке на Земле, на основе чего определяется угол р отражения от поверхности Земли (рис. 1). Источник прямого излучения от Солнца моделируется в виде параллельного пучка частиц (вектор q^.

Величина угла а между направлениями из разыгранной точки на объект РО' и из центра Земли на объект ОО', который определяет искомое направление излучения от Земли, вычисляется исходя из следующего соотношения (см, например, [9]):

1 — cos 7max COS 7

cos а = —                                 :, у/1 + (cos 7max)2 — 2 COS 7max COS 7

где R - радиус Земли, H - высота орбиты.

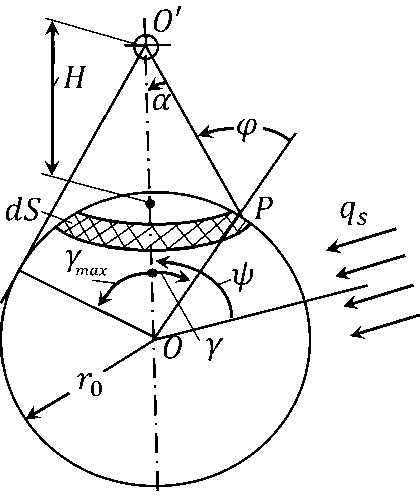
Рис. 1. Схема облучения КА отраженным солнечным излучением; репродукция из [10]

Пространственная протяженность освещаемых Солнцем областей, попадающих на искомый объект, в общем случае зависит от его положения относительно Солнца и Земли. В частности, от направления падения солнечных лучей относительно оси, соединяющей центр КА и центр Земли (угол ^ на рис. 1). Поэтому далее проводится оценка, может ли попасть излучение от Солнца в разыгранную точку на поверхности Земли, т.е. может ли указанная точка быть источником отраженного солнечного излучения. Для этого определяется угол между векторами направления падения солнечного излучения на Землю qs и разыгранным ранее направлением из точки на поверхности Земли на центр объекта РО' (рис. 1). Значение данного угла, равное 90°, характеризует границу освещения поверхности Земли Солнцем (через нее проходит касательная от Солнца). Если указанный угол больше 90°, то поверхность Земли в данном направлении не освещается Солнцем и разыг ранная точка не дает вклада в излучение, отраженное от Земли. Подобные траектории прерываются. В противном случае проводится дальнейшее моделирование траектории ча стицы исходя из разыгранных ранее параметров, а именно, для полученного направления облучения равномерно по площади проекции объекта определяются начальные координаты частицы.

Описанная математическая модель была реализована в рамках комплекса POKC-RG [6], разработанного для расчета распространения оптического излучения в трехмерной среде, и использует метод Монте-Карло в приближении геометрической оптики. Геометрия трехмерных объектов в программе описывается в виде уравнений поверхностей второго по рядка, что позволяет существенно экономить расчетное время по сравнению с воксельным представлением.

3.    Результаты исследований

В качестве объекта исследований рассматривалась круговая цилиндрическая бленда с тремя внутренними диафрагмами, которая обычно является составной частью объективов звездных датчиков. Основными габаритными параметрами бленды являются радиусы входного и выходного отверстий, ее длина и угол поля зрения. К техническим характеристикам бленды также относят такие величины, как угол прямой засветки и угол допустимой засветки. Первая из указанных величин характеризует максимальный угол, при котором наблюдается пространственная неоднородность в распределении плотности потока на выходе бленды, его величина определяется максимальным углом между оптической осью и лучом, соединяющим кромки входного и выходного отверстий. Вторая величина характеризует угол, при котором коэффициент ослабления бленды достигает требуемого по условиям задачи значения.

Общий вид бленды, выполненный специально разработанным для программы РОКС-RG способом визуализации [13], показан на рис. 2. При проведении исследований было принято, что материал внутреннего покрытия бленды обеспечивает диффузный характер отражения, с коэффициентом отражения, равным 3%. Угол прямой засветки выбранной конструкции составил 36°.

Упрощенная схема условий облучения бленды излучением от Земли представлена на рис. 3. Начало локальной системы координат бленды располагали на ее входе. Ось z совпадала с оптической осью бленды и была направлена вне бленды. Направление осей х и у ввиду симметрии объекта определялось произвольно исходя из правой системы координат. При проведении исследований направление оси z варьировалось относительно направления на центр Земли, направления осей х и у пересчитывались соответствующим образом.

Обозначим угол между направлением оптической оси бленды (ось z) и направлением на центр Земли (в надир) символом (3. Угол (3 = 90° будет соответствовать условиям облучения со стороны Земли, когда ось х в системе координат объекта направлена на центр Земли (в надир). Значения углов (3 <  90° - условиям облучения, при которых оптическая ось отвернута от поверхности Земли, а значения (3 >  90° - условиям, при которых оптическая ось повернута к Земле. Угол между направлением оптической оси бленды и направлением облучения со стороны Солнца обозначим символом в'. Значение О' = 90° будет означать облучение Солнцем в направлении оси х бленды. Для удобства дальнейшего изложения введем также угол 0_sun = О' — 180°. У гол 0_sun = 0° будет означать облучение бленды вдоль оптической оси со стороны входного отверстия, a d_sun = 180° - со стороны, противоположной входному отверстию бленды.

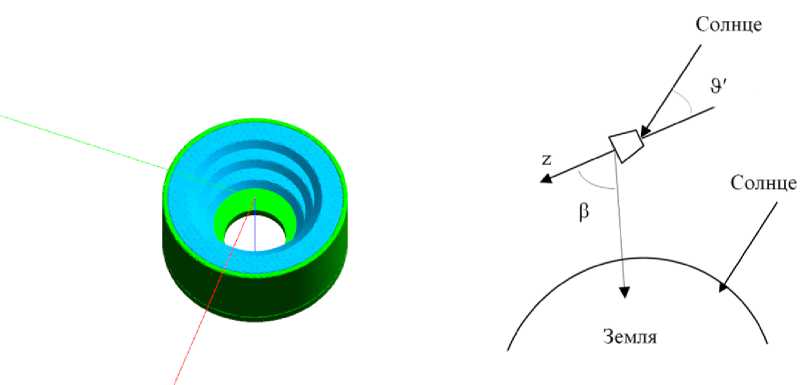
„   _ „      „                              Рис. 3. Взаимное расположение

Рис. Внешний вид олепды                <      п

олепды, Земли и Солнца

4.    Оценка влияния угловой неоднородности отраженного солнечного излучения на коэффициент ослабления бленды

Оценка эффективности бленды, как указывалось выше, проводится путем определения кратности ослабления мононаправленного излучения, ориентированного под различными углами относительно оптической оси бленды, усредненной по ее выходному отверстию. По аналогии с указанной оценкой (назовем ее стандартной) проведем оценку эффективности для источника светового излучения, отраженного от поверхности Земли. Для этого рассчитаем коэффициент ослабления бленды в зависимости от угла поворота ее оптической оси относительно направления на Землю. При этом в качестве нулевой точки отсчета углов примем ориентацию, при которой оптическая ось бленды направлена на центр Земли. Положение Солнца - над блендой, на одной прямой с ее центром координат и центром Земли.

На рис. 4 показана зависимость коэффициента ослабления выбранной нами бленды от угла падения параллельного пучка частиц относительно оптической оси, а также зависимости коэффициентов ослабления отраженного от Земли излучения для объекта на орбитах высотой 600 км и 900 км.

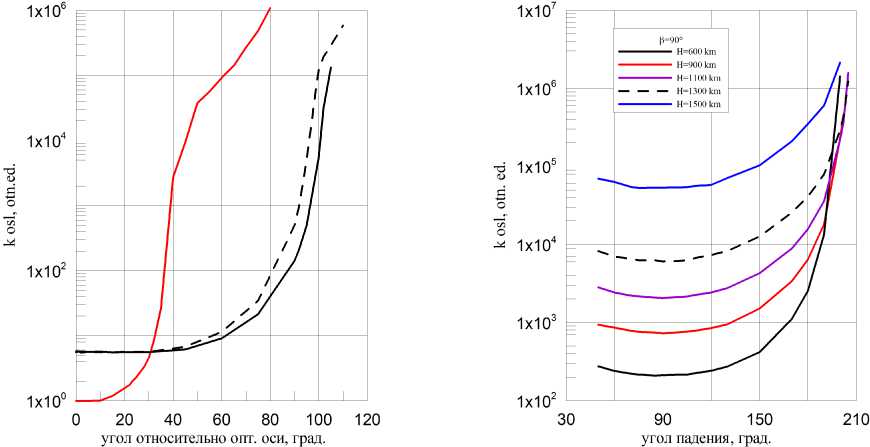
Рис. 4. Угловая зависимость коэффициента ослабления бленды: красный - параллельный пучок, черный - расходящийся (излучение, отраженное от Земли); сплошная - Н = 600км, пунктир - 900 км

Рис. 5. Коэффициент ослабления k_osi_es в зависимости от угла падения Солнца относительно оптической оси бленды 3_sun

Примем, что по условиям задачи нам необходим коэффициент ослабления, равный 2.5е3. Согласно рис. 4 соответствующее значение угла допустимой засветки при облучении бленды параллельным пучком частиц составит 40о. Для зависимостей, относящихся к источнику со стороны Земли, видно, что выбранный уровень коэффициента ослабления достигается при значениях поворота оптической оси на углы, превышающие 90о, т.е. когда оптическая ось отвернута от Земли.

На практике во избежание засветки от Земли при выборе направления оптической оси прибора относительно направления в надир принято ориентироваться на условия облучения, при которых в конус поля зрения оптического датчика ц не попадает излучение, отраженное от поверхности Земли. Для этого угол /3 между направлением оптической оси прибора и направлением на центр Земли должен превышать величину 3min₅ равную сумме угла полураствора конуса видимости поверхности Земли с поверхности КА 3о = ^/2 — 7m_ax и половине угла поля зрения оптики ц/2. Задаётся также некоторый запас в значении угла 3mi_n? чтобы убрать возможное попадание в поле зрения датчика светового нимба Земли [14,15]. В нашем случае в качестве угла поля зрения оптики был выбран угол прямой засветки 3za_sw рассматриваемой бленды, равный 36°. Значения вышеперечисленных углов ymax, 30? 3m_in = 30 + 36^о, для орбит различной высоты представлены в табл. 1.

Их анализ показывает значительность углового размера небесной сферы, недоступной для определения ориентации на низких орбитах функционирования КА с помощью звездных датчиков. В то же время представленные значения граничных углов получены для условий максимальной засветки, когда Солнце находится над объектом, т.е. дают консер-

Таблица 1

Значения углов, определяющих засветку от Земли

Н, км 7max, град. 3о = 90 - 7max, град. Amin = 3о + 36°, град. 600 29.94 66.06 102.06 900 28.80 61.20 97.2 1100 31.47 58.53 94.53 1300 33.82 56.18 92.18 1500 35.93 54.06 90.06 2000 40.42 45.57 81.57 вативную оценку. Но в процессе вращения вокруг Земли направление облучения КА со стороны Солнца непрерывно меняется. И возможна реализация условий облучения, при которв1х допустимая засветка будет обеспечиватвся при меньших значениях углов ориентации оптической оси относительно направления в надир.

Для оценки влияния неоднородности облучения бленды за счет изменения положения Солнца были проведены исследования по формированию ее коэффициента ослабления (k_osi_es) для различных углов падения лучей от Солнца d_sun относительно ее оптической оси, а также для различных направлений оптической оси (угол /3) относительно Земли. В качестве начальной ориентации рассматривалась ситуация, при которой оптическая ось была перпендикулярна направлению в надир, т.е. значение 3 = 90°.

На рисунке 5 приведены зависимости коэффициентов ослабления от угла падения лучей от Солнца относительно оптической оси бленды для орбит в диапазоне высот 600 ... 1500 км при значении угла /3 = 90°. Отсчет углов на оси х начинается не с нуля, поскольку при малых значениях d_sun основная засветка будет от Солнца, а не от Земли (значения угла d_sun, меньшие 90°, соответствуют нахождению Солнца в передней полусфере относительно входного отверстия бленды).

Видно, что для каждой из рассмотренных высот орбиты наибольшая засветка излучением от Земли, соответствующая минимальному значению коэффициента ослабления, происходит для направления облучения при d_sun = 90°. В этом случае Солнце находится над объектом и практически вся освещаемая им поверхность Земли является источником отраженного излучения для объекта на орбите. Наименьшая засветка наблюдается в случаях, когда Солнце находится в задней полусфере относительно входного отверстия бленды в области углов d_sun порядка 180° и выше, поскольку в этом случае на вход бленды попадает лишь небольшая часть излучения от освещаемой Солнцем Земли.

Если в качестве эквивалентности условий облучения для параллельных пучков и расходящегося излучения от Земли исходить из равенства значений коэффициента ослабления бленды, то из приведенных рисунков следует, что условия максимальной засветки от Земли (/3 = 90° и d_sun = 90°) обеспечивают допустимую засветку для орбит высотой 1100... 1200 км и более. На меньших высотах величина засветки от Земли слишком велика и для ее снижения необходима иная ориентация. Проверим высказанное предположение об эквивалентности условий облучения.

5.    Расчет пространственных распределений излучений на выходе бленды

Кратность ослабления бленды согласно своему определению является интегральной величиной для светового потока на ее выходе в области размещения линзы. Очевидно, что излучение от боковых помех, проходящее внутрь бленды, неравномерно освещает выходное отверстие. Рассмотрим, насколько различается указанная неравномерность для параллельных и расходящихся пучков и, соответственно, можно ли в качестве эквивалентности указанных условий облучения исходить из равенства кратностей ослабления бленды.

С этой целью были проведены исследования пространственного распределения освещенности по месту размещения первой линзы на выходе бленды. Радиус выходного отверстия был выбран равным 0.5 см. Массив ячеек регистрации сформировали в результате деления плоскости выходного отверстия на кольца равной площади по радиусу, а каждый из колец - на сектора по азимутальному углу. В частности, были выделены слои толщиной 0 ... 0.22 см, 0.22 ... 0.316 см, 0.316 ... 0.387 см, 0.387... 0.44 см, 0.44 ... 0.5 см, каждый слой был разделен на 12 частей.

Для сравнения пространственных распределений для мононаправленного и расходящегося излучений наиболее подходящими являются условия облучения, которые дают примерно одинаковый интегральный коэффициент ослабления. В качестве сопоставляемых условий облучения были выбраны условия облучения бленды пучком мононаправленных квантов под углом 40° относительно оптической оси (угол допустимой засветки) и условия облучения излучением от Земли на высоте 1100 км с ориентацией оптической оси бленды под углом /3 = 90о. В обоих случаях интегральный коэффициент ослабления составил величину, примерно равную 2.5е3 .

Результаты расчета пространственного распределения излучения для сопоставляемых условий облучения представлены на рис. 6. В частности, на рис. 6а показано распределение плотности потока в зависимости от азимутального угла размещения детекторов во внешнем слое, а на рис. 66 - в среднем слое детекторов.

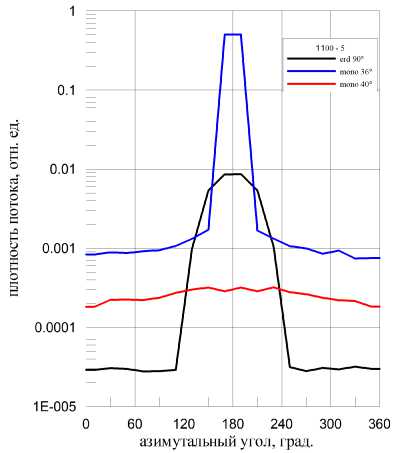
Рис. 6а. Плотность потока квантов в зависимости от азимутального угла для внешнего слоя детекторов (г = 0.44... 0.5 см); высота орбиты 1100 км

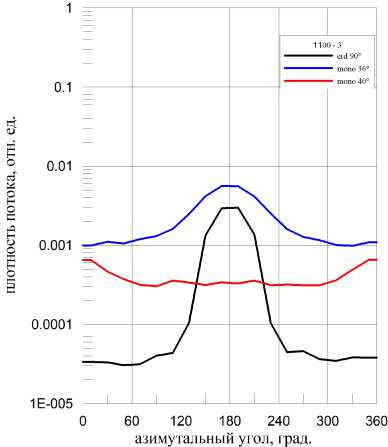
Рис. 66. То же, что на рис. 6а, для внутреннего слоя детекторов (г = 0.316 ... 0.387 см)

Следует иметь в виду, что для наглядности результаты расчетов, представляющие усредненные по площади детекторов величины, показаны в виде сглаженных кривых, а не гистограмм. На рисунках видно, что в случае мононаправленного источника для угла допустимой засветки (40о) распределение потока в плоскости по месту размещения линзы примерно равномерное по площади отверстия, а для сопоставляемой зависимости плотности потока за счет отраженного от Земли излучения распределение имеет ярко выраженный максимум. Его величина выше значения потока для угла допустимой засветки от параллельного пучка частиц в 10... 50 раз. На обоих рисунках также показаны зависимости излучения, падающего параллельным пучком частиц под углом прямой засветки, для которых, как и следовало ожидать, пространственное распределение имеет значительный максимум, особенно на краях отверстия.

Таким образом, равные значения коэффициента ослабления бленды для параллельного пучка частиц и солнечного излучения, отраженного от поверхности Земли, не свидетельствуют об эквивалентности указанных условий облучения для уровня допустимой засветки. Локальные засветки, связанные с пространственно-угловой неоднородностью излучения, отраженного от Земли, имеют более выраженный характер, чем неоднородности для мо-нонаправленного источника. Совокупный анализ интегральных значений коэффициентов ослабления и их пространственных распределений по месту размещения первой линзы показал, что допустимая засветка для условий облучения со стороны Земли обеспечивается при значениях коэффициентов ослабления, определяемых на основе параллельного пучка частиц, примерно в 3... 5 раз больших, чем при существующем стандартном подходе.

Влияние различных ориентаций оптической оси относительно Солнца и Земли на зависимости пространственного распределения плотности потока излучения по месту размещения линзы рассмотрим для орбиты высотой 600 км. Соответствующие результаты приведены на рис. 7а, б, в. В частности, на рис. 7а показана вариация пространственных распределений для различных значений угла поворота оптической оси относительно направления на центр Земли /3 при направлении падения солнечного излучения перпендикулярно оптической оси ( 0_sun = 90°). Видно, что, как и ожидалось, поворот оптической оси на угол, превышающий граничный угол 102.06° (см. табл. 1), обеспечивает допустимую засветку бленды.

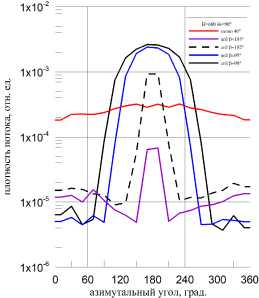
Рис. 7а. Азимутальная зависимость плотности потока квантов во внешнем слое для Osun = 90^о и различных углов /3; высота орбиты 600 км

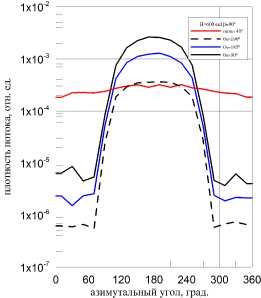
Рис. 76. То же, что на рис. 7а, для 3 = 90^о и различных углов Osun

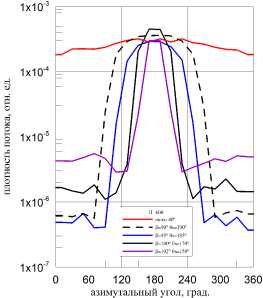
Рис. 7в. То же, что на рис. 7а, для различных углов O_sun и 3

На рисунке 76 приведены результаты расчетов для одной и той же ориентации оптической оси относительно направления на Землю и различных условий облучения со стороны Солнца. В качестве базовой была выбрана ориентация оптической оси перпендикулярно направлению на центр Земли ( 3 = 90°). Анализ данных рисунка показывает, что даже для указанной ориентации оптической оси имеются направления облучения со стороны Солнца, обеспечивающие допустимую засветку (пунктир). По мере увеличения угла 3 ^в интервале 90° < 3 <  (3mi_n = 102.06°) дополнительная область угловых направлений облучения со стороны Солнца, обеспечивающих допустимую засветку, растет, что наглядно показано на рис. 7в.

6.    Определение угловых областей, обеспечивающих допустимую засветку при моделировании траектории

Для оценки величины дополнительной угловой области направлений облучения со стороны Солнца, обеспечивающих допустимую засветку, было проведено численное моделирование траектории КА с заранее заданными исходными данными по параметрам орбиты на время одного оборота объекта вокруг Земли. На базе указанного моделирования для каждого заданного момента времени движения КА формировались массивы данных по источникам облучения со стороны Земли и проводились расчеты соответствующих плотностей потока по месту размещения первой линзы в бленде. При моделировании траектории объекта предполагалось, что ось X бленды была направлена в надир, а оптическая ось ориентировалась перпендикулярно направлению в надир. Результаты расчетов для орбит высотой 600 и 900 км представлены на рис. 8 в виде зависимостей плотности потока от угла между направлениями на центр Земли и на Солнце (угла г‘ = тг — гр).

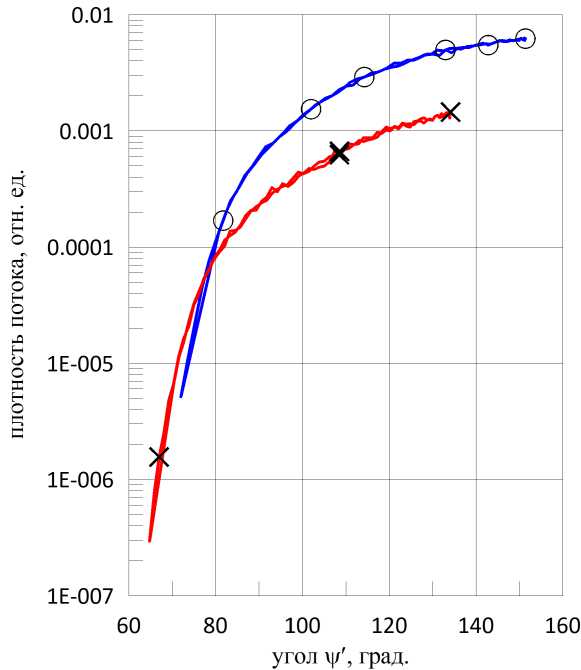
Рис. 8а. Плотность потока внутри бленды на высоте КА 600 км (о) и 900 км (х) при наличии теневой области на орбите

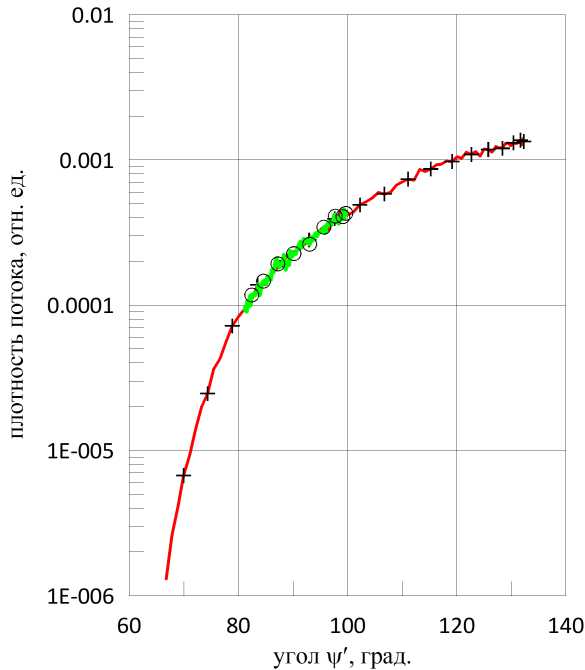
Рис. 86. Плотность потока внутри бленды при движении КА на высоте 900 км при наличии теневой области (+) и без нее (о)

Их анализ показал, что дополнительные угловые области, обеспечивающие допустимую засветку, непосредственно примыкают к области тени на орбите, как бы расширяя теневую область. При этом указанные дополнительные области относятся к ситуациям на орбите, когда угол между направлением в надир и на Солнце меньше 80о. В случае отсутствия теневой области на орбите дополнительные угловые области с допустимой засветкой отсутствуют.

7.    Выводы

Проведенные в работе исследования по засветке бленды в условиях облучения солнечными лучами, отраженными от поверхности Земли, показали следующее.

Равенство коэффициентов ослабления бленды для параллельного пучка частиц и для солнечного излучения, отраженного от поверхности Земли, не является показателем эквивалентности условий облучения в связи с различием пространственной неоднородности полей излучений на выходе бленды. При оценке допустимой засветки выходного отверстия бленды отраженным от Земли солнечным излучением на основе данных, полученных для параллельного пучка лучей, следует ориентироваться на кратность ослабления, большую примерно в 3 ... 5 раз.

Показано, что стандартная консервативная оценка угловой области облучений, обеспечивающей допустимую засветку, на основе выбора области направлений оптической оси относительно направления на центр Земли, образующих угол, равный /3min = f30+/3zasw, в ряде случаев является завышенной. Для каждой из ориентаций из диапазона 90о < ft < ^min при наличии теневых участков орбиты существует дополнительная область угловых направлений оптической оси относительно Солнца, также обеспечивающая допустимую засветку. Предварительный анализ ориентации орбиты, ориентации КА на орбите относительно Солнца и местоположения звездного датчика на объекте может позволить увеличить угловой размер небесной сферы, доступной для определения ориентации.

Дальнейшие исследования предполагается проводить в направлении реализации полученных результатов для конкретных практических ситуаций.