Особенности зондовых методов локального измерения коэффициента холла

Измерения одних из основных кинетических коэффициентов полупроводниковых монокристаллов таких, как коэффициент Холла и удельная электропроводность, позволяют получать информацию о концентрации и подвижности свободных носителей заряда. Для определения электропроводности в настоящее время широко используются зондовые методы благодаря их простоте, надежности и воспроизводимости [1-4]. Однако измерение коэффициента Холла с помощью зондов в настоящее время сдерживается ввиду громоздкости математических выражений для поправочных множителей, входящих в расчетные формулы.

В данной работе ставится цель - усовершенствовать существующую методику зондовых методов измерений коэффициента Холла для изотропных полупроводников в направлении ее физической ясности, простоты и точности [1]. Для достижения этой цели нами предложена довольно простая теоретическая модель определения эффекта Холла, которая содержит минимум упрощающих предположений, приводит к физически простым и ясным результатам.

Расчеты выполнены применительно к пластинам и слоям, размеры которых значительно больше их толщины. В этих случаях распределение потенциала в исследуемых образцах является двумерных. Математическая

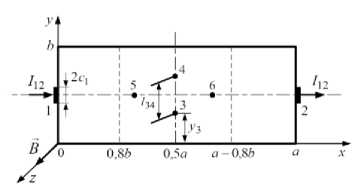
Рис. 1 Схема расположения контактов на полупроводниковом образце

модель предполагает измерение э.д.с. Холла в области относительно слабых магнитных полей, когда можно пренебречь эффектом магнетосопротивления и пригодна только в том случае, когда расстояние между измерительными зондами много больше, чем длина свободного пробега носителей заряда [3].

В рассматриваемом случае по прямоугольному изотропному образцу, электропроводимостью σ, протекает постоянный ток через контакты 1 и 2, расположенные на периметре образца (рис. 1). Толщина кристалла d меньше его длины а и ширины b. Магнитное поле индукцией В направлено перпендикулярно плоскости образца вдоль оси OZ. При этих условиях выражение для потенциала р в области полупроводника удобно представить в следующем виде

Р(х,у) = (о(х,у) + Рн(х,у);

Ро(х,у) = ^L. ста

Здесь р0(х, у) - есть потенциал электрического поля в образце при отсутствии внешнего магнитного поля, р(х, у)- потенциал поля Холла, которое возникает после включения внешнего магнитного поля.

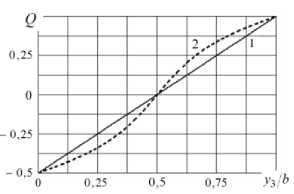
Рис.2 Зависимость множителя

Q от ^у 3 /_ь для различных значений координаты x.

На рис. 2 представлен график зависимости безразмерного множителя Q от относительной координаты холловского зонда у3/^ для различных значений координаты x: линейная зависимость 1 для средней части образца в области значений 0,8 ≤ x ≤ (a - 0,8 b); кривая 2 в приконтактной области при x=0,2b.

Из графиков следует, что в средней части образца в области 0,8 ≤ x ≤ (a - 0,8 b) ряд в правой части равенства пренебрежимо мал, поэтому с погрешностью менее 1% потенциал поля Холла рн зависит от у линейно, т.е. определяется выражением:

I КВу-0,5Ь Рн(у) =   ,      /  .

а     b

Распределение потенциала поля Холла в областях растекания тока вблизи токовых контактов является более сложным.

Из рис. 2 видно, что зависимость

Q (^{У з} /ь)

в приконтактных областях

является существенно нелинейной.

Из проведенного анализа результатов компьютерного моделирования полученных математических выражений можно предложить следующую методику совместного измерения коэффициента Холла и электропроводимости в изотропных полупроводниках.

• 1.    Расположить токовые контакты 1 и 2 и измерительные зонды 3 и 4 согласно схеме на рис. 1. Измерить расстояние между зондами l ₃₄.

• 2.    Через токовые контакты 1 и 2 пропустить постоянный ток I 12 и измерить разность потенциалов U 04 между зондами 3 и 4 при отсутствии внешнего магнитного поля.

• 3.    Затем образец поместить в поперечное относительно слабое магнитное поле и при том же токе I ₁₂ измерить разность потенциалов U ₃₄ между зондами 3 и 4 в магнитном поле. Э.д.с. Холла при этом равна разности измеренных значений E H = U 34 -U 34 .

• 4.    Вычислить коэффициент Холла R :

EHdb !'=^вГ

Для этого при токе I12 через контакты 1, 2 измеряем разность потенциалов U56 между зондами 5 и 6, расположенными в выделенной области 0,8b ≤ x ≤ (a - 0,8b), при отсутствии внешнего магнитного поля и расстояние   l56 между ними (рис. 1). Удельная электропроводность материала образца вычисляется по формуле

_ ^ 12 ^ 56 ° = U₅₆db

Следует заметить, что представленная методика означает распространения известного двухзондового метода измерения электропроводимости полупроводниковых образцов на определение коэффициента Холла.

Отметим некоторые практические рекомендации по реализации данной методики.

При проведении экспрессных измерений в качестве токовых контактов удобно использовать прижимные заточенные зонды, смещенные на некоторую величину ∆ x от границ образца.

Следует отметить полезное для практики правило обратимости токовых и измерительных зондов, которое заключается в следующем. Если пропускать ток I ₁₂ через контакты 1 и 2, то величина э.д.с. Холла между контактами 3 и 4 в магнитном поле будет составлять некоторое значение E ₃₄. Если затем пропускать такой же ток через контакты 3 и 4 ( I ₁₂= I ₃₄) в таком же магнитном поле, то между контактами 1 и 2 возникает э.д.с. Холла E 12 , равная по величине E 12 = E 34 . Если в процессе измерений данное равенство выполнено, то это будет дополнительно свидетельствовать об однородности исследуемого образца и повысит достоверность получаемых результатов. Правило обратимости токовых и измерительных зондов при измерениях эффекта Холла доказывается как теоретическими расчетами, так и экспериментальными измерениями. Данное правило полезно для контрольных измерений на полупроводниках.