Особые положения технологического оборудования с параллельными приводами рабочего органа

В современном машиностроении применяется оборудование, рабочий орган которого связан с основанием несколькими кинематическими цепями, часть из которых имеет приводы [4]. Достоинствами такого оборудования являются высокая жесткость и точность перемещений рабочих органов, малая металлоемкость, недостатками - сложность управления, относительно небольшое рабочее пространство и сложная его форма, а также наличие особых положений, при которых координаты входных звеньев становятся зависимыми друг от друга. Одним из критериев особого положения является равенство определителя матрицы Якоби (якобиана) нулю [1,6].

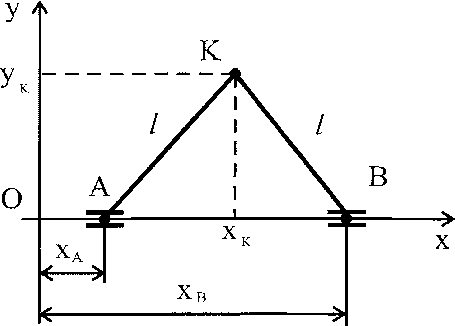
Рис. 1. Кинематическая схема двухкоординатного исполнительного механизма

Определим особые положения двухкоординатного         исполнительного механизма с параллельными приводами (рис. 1).

Данный механизм состоит из ползунов А и В, которые перемещаются по оси Ох и соединены пальцем штангами постоянной длины. Примем длины штанг АК и В К одинаковыми и равными I.

При решении прямой задачи геометрического анализа [6] исследуемого механизма функции положения имеют вид:

хк =^(ха+хв);

I —7-----v                                             ⁽¹⁾

v I Хв Хд I Ук р ~      •

Якобиан для системы (1)

5х_к дх_к дх_А дх_в дУк дУк дх, дх_в

хВ-ха

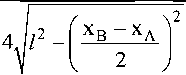
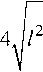
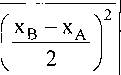
ХА-ХВ

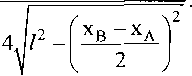
Из равенства

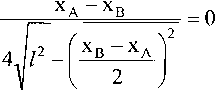
следует, что в особом положении х_А = х_в входные звенья А и В находятся в одной точке (рис. 2, а, б). В данном положении механизм теряет управляемость - «сдвоенная» штанга длиной I может занимать произвольное положение, вращаясь вокруг нижнего «сдвоенного шарнира» АВ.

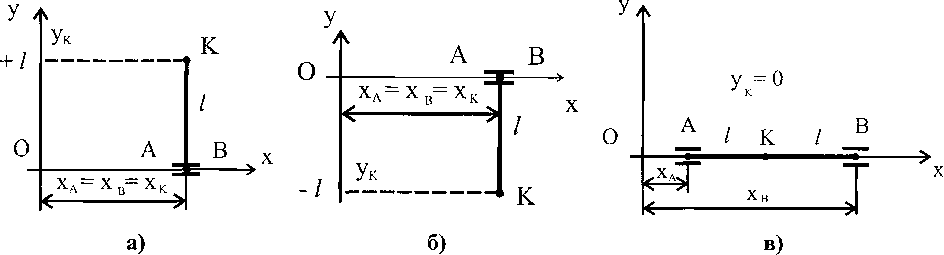
Рис. 2. Особые положения двухкоординатного исполнительного механизма

При решении обратной задачи геометрического анализа исследуемого механизма функции положения таковы:

ХА = ХК хв = хк + Ф “ Ук-

Якобиан для системы (3)

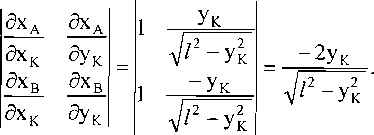
Из равенства

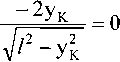
следует, что в особом положении ук = 0 - точки А, В и К находятся на оси Ох (рис. 2, в). В данном положении шарнир К может перемещаться только вдоль прямой, соединяющий шарниры А и В. Координаты хА и хв зависимы.

Итак, особые положения такого механизма:

• 1)    центры шарниров А и В находятся в одной точке (рис. 2, а, б);

• 2)    точки А, В и К находятся на одной прямой (рис. 2, в).

  

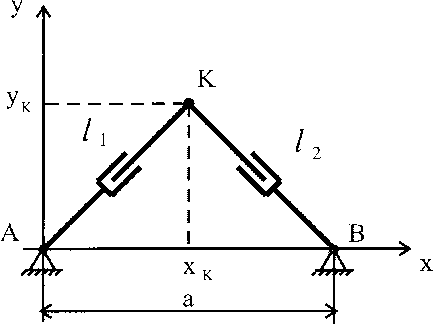
  Рис. 3. Кинематическая схема двухкоординатного исполнительного механизма с переменными длинами штанг

  
  

В результате расчетов при решении прямой задачи геометрического анализа был найден один вариант особых положений двухкоординатного исполнительного механизма с параллельными приводами, а при решении обратной задачи геометрического анализа -другой вариант. Это связано с тем, что в первом случае входными координатами данного механизма являются координаты ползунов А и В - хА и хв, выходными координатами -координаты шарнира К - хк и ук, а во втором случае - наоборот.

Проведем исследование особых положений другого двухкоординатного исполнительного механизма с параллельной кинематической структурой (рис. 3).

Звено такого механизма - шарнир с центром в точке К соединяется с основанием с помощью двух стержней АК и ВК изменяемой длины /1 и /2. Координаты шарниров А и В примем еле-дующими: хА = 0, уА = 0, хв = а, ув = 0.

При решении прямой задачи геометрического анализа исследуемого механизма функции

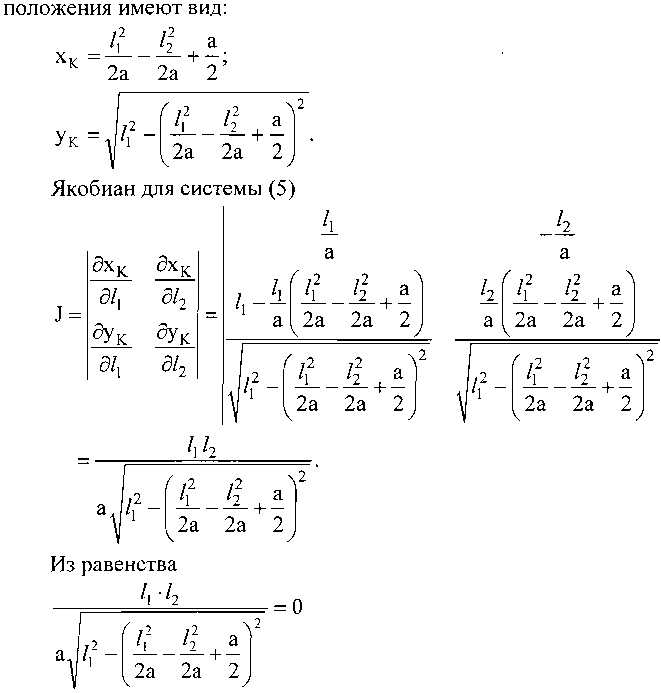
следует, что в особых положениях у исследуемого механизма либо длина штанги АК 7] = 0,72 = а, хк = Ук = 0 (рис. 4, а), либо длина штанги ВК 72 =0,7] = а, хк =а, ук = 0 (рис. 4, б).

При решении обратной задачи геометрического анализа исследуемого механизма функции положения примут вид:

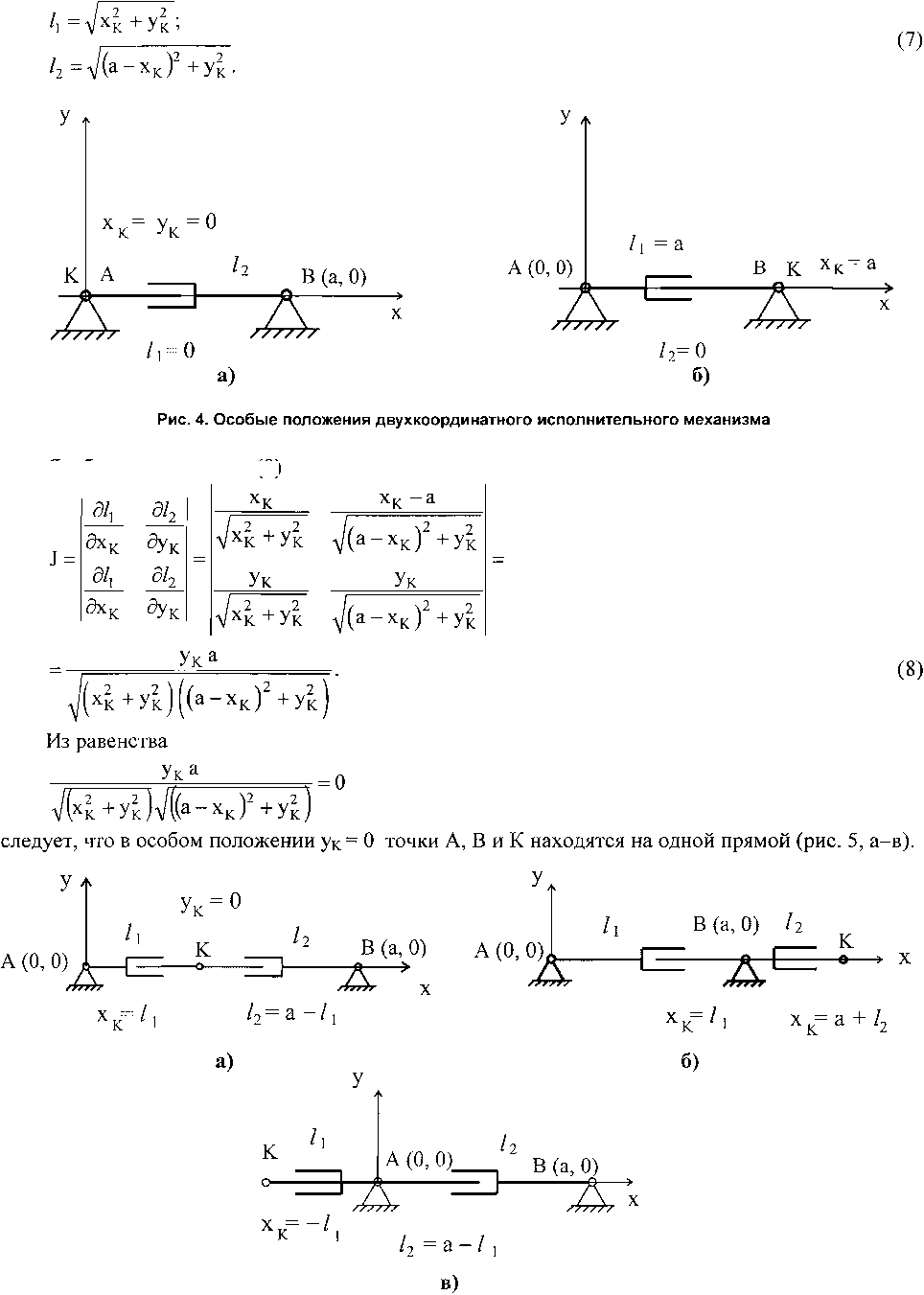
Якобиан для системы (8)

Рис. 5. Особые положения двухкоординатного исполнительного механизма с переменными длинами штанг

В более сложных случаях функции положения определяются в неявном виде [6]. Так, когда переменная у, являющаяся по смыслу задачи функцией аргументов х15х2,...хп, задается посредством функционального уравнения

Р(у,х1,х2,...хп) = 0, (9) говорят, что у как функция аргументов х1? х2,...хп задана неявно [2]. Для m функций (при ш = п) Fb F2, ..., Fm можно составить определитель Якоби (якобиан):

дУ1   9У2      дут

9F2   dF2        5F2

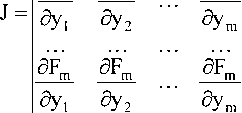
Функции положения в неявном виде для двухкоординатного исполнительного механизма с переменными длинами штанг (рис. 3) имеют вид:

Е =х| +ук — А2 =0;

/ V 2    2                                                                           <¹⁰>

Р2 = (а-хк) + ук -Z2 =0.

При решении прямой задачи геометрического анализа (при задании функции положения в неявном виде) определитель Якоби для системы (10)

дЦ 5^

-2^   0

0   -2Z2

(H)

9/j    5Z2

dF2 5F2

5Zf dZ2

Приравняв определитель (И) нулю, получим

4/Д2=0.                                                                        (12)

Чтобы найти координаты, соответствующие особому положению согласно [3], нужно выражение (12) объединить с одним из уравнений системы (10) и найти их совместное решение.

В результате исследований получим следующие варианты особых положений двухкоорди натного исполнительного механизма с параллельными приводами:

• 1)    длина штанги АК Л = 0, Z₂ = а, х_к = ук= 0 (см. рис. 4, а);

• 2)    длина штанги В К Z₂ =0, 1^ = а, х_к =а, ук= 0 (см. рис. 4, б).

При решении обратной задачи геометрического анализа исследуемого механизма определитель Якоби для системы (10) (при задании функции положения в неявном виде) имеет вид

а^ а^

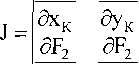
дхк дук

^хк 2ук 2(хк-а)

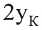
= 4ук а.

Приравняв определитель (14) нулю, получим

4ука = 0.                                                                       (14)

Найдем координаты, соответствующие особому положению. Согласно [3] нужно выражение (14) объединить с одним из уравнений системы (10) и найти их совместное решение.

В результате исследований получили следующие варианты особых положений двухкоординатного исполнительного механизма с параллельными приводами: ук=0, хк =± /ь xK=a±Z2, точки А, В и К находятся на одной прямой (см. рис. 5, а-в).

В результате исследований получили особые положения двухкоординатных исполнительных механизмов с параллельными приводами. Как следует из изложенного выше, процесс вычисления является сложным для рассмотренных простейших случаев. Однако для управления такими механизмами необходимо знать их особые положения, так как в этих положениях теряет-

Сюськина Ю.Л.                           Особые положения технологического оборудованияс параллельными приводами рабочего органа ся управляемость механизмов и имеют место неблагоприятные условия для передачи сил и моментов [1, 4-6].

Поэтому варианты особых положений механизма с параллельными приводами можно найти по следующему алгоритму:

• 1)    составить функции положения в явном или неявном виде по кинематической схеме механизма;

• 2)    определить якобианы при решении прямой и обратной задач геометрического анализа и приравнять их нулю;

• 3)    найти координаты, соответствующие особому положению.