Осторожно, человеко-годы! Опыт наблюдения парадокса Симпсона в эпидемиологических исследованиях риска

Категория «человеко-годы» [9] исторически возникла в связи с анализом риска возникновения нежелательных последствий для здоровья – сначала в популяционных исследованиях, а затем и в когортных. Эпидемиологический словарь определяет это понятие, как «человеко-время (person-time) – измерение, комбинирующее людей и время в качестве знаменателя при вычислении инцидентности и смертности …, когда отдельные лица испытывают риск развития заболевания или смертельного исхода в течение разного времени. Это сумма всех отрезков времени, в течение которых все лица находились под риском». По-видимому, первым исследователем, фактически использовавшим понятие в середине XVII в., был Джон Граунт [3]. Количество человеко-лет наблюде- ния традиционно применялось и применяется для оценок интенсивности смертности или заболеваемости, которые многие практикующие эпидемиологи прямо связывают с терминами «риск» или «показатель риска»:

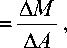
где ∆ M - число «случаев» за период наблюдения; ∆ A – количество человеко-лет наблюдения.

Заметим, что величина λ вошла в оборот еще до начала бурного развития математики, вызванного открытием дифференциального и интегрального исчислений, а также теории вероятности и математической статистики. Англоязычные справочники также определяют

показатель как stratum-specific rate , или как hazard . Именно демографы подтолкнули поиск его приложений как в области дескриптивной статистики, так и математической [3]. Известно, что и само слово «статистика» впервые было использовано Готфридом Ахенваллем в 1746 г. в качестве эквивалентного названия дисциплины «государствоведение» в Марбургском и Геттингенском университетах, то есть в дескриптивном смысле.

Современная теория риска меняет парадигму XVII–XVIII вв., ставя во главу угла категорию вероятности, определяя риск как вероятность наступления нежелательных событий (при комбинации условий – то есть как условную вероятность) [1]. Для научной демографии и доказательной эпидемиологии это особенно актуально, если речь идет об определении возможного вреда здоровью под влиянием таких факторов и в таких условиях, когда персональный ущерб объективно измерить невозможно, но возможно количественно определить закономерности изменения стохастической выживаемости большой группы людей или наступления отдаленных последствий. Поиски научного подхода к измерению такого рода биологических эффектов интенсифицировались с 70-х гг. прошлого столетия в связи с повсеместным ростом химических, фармакологических, радиационных, экологических и прочих техногенных рисков.

На первый взгляд, смена научной парадигмы никак не противоречит категории человеко-лет, поскольку распределение членов однородной изучаемой когорты можно описать функцией распределения по возрасту t :

F ( t ) = 1 - exp

(         ^

- j X( t ) d т

к о        7

где λ( t ) – интенсивность смертности от всех причин; F ( t ) - риск смерти и он же - функция распределения. При этом Х( t ) = = F'(t )/ ( 1 - F ( t ) ) или X( t ) = - S'(t )/ S(t ), где S ( t ) - функция выживания S ( t ) = 1 - F ( t ).

Функция распределения и функция выживания оцениваются эмпирически. Благодаря этому, на любом конечном интервале наблюдения A t при достаточной величине изучаемой выборки N ₀ вместе с условием N ( t ) ~ N ₀ S ( t ) можно прийти к формуле (3):

Х( t ) = - S '( t )/ S ( t ) «

N ₀( S ( t + A t ) - S ( t )) _ _A N _AM (3) ~ N ₀ S ( t ) A t ” AA ~ AA "

Таким образом, в описательном смысле понятия риска и интенсивности риска равноправны. Казалось бы, остается подобрать группу сравнения и сделать выводы. Однако практика применения убеждает нас, что это было бы неверно. И дело не только в том, что отношения интенсивностей рисков и самих рисков в изучаемой группе и группе сравнения различны по смыслу и по величине, но также в том, что каждый из этих показателей определен для однородной группы, а сами показатели должны отличаться только одним изучаемым фактором. Однако именно это обстоятельство исследователями не всегда строго контролируется.

Цель работы – указать на типичные примеры наблюдения парадокса Симпсона при сравнении неоднородных групп, когда неоднородность наблюдается более чем по одному фактору, контролируемому исследователем. Этот парадокс известен еще со времен Карла Пирсона (1900), однако неоднократно «переот-крывался». Неконтролируемые факторы общеизвестны также под именем «мешающих» переменных. Метод сопоставления исследуемой группы и контрольной фактически приводит к оценкам таблиц сопряженности. Они строятся как на принципе непосредственного сопоставления рисков (классические таблицы сопряженности), так и на принципе сопоставления интенсивностей наблюдения событий. В последнем случае как раз и применяется категория человеко-лет. Для иллюстрации математических артефактов, к которым относится парадокс Симпсона, рассмотрим табл. 1.

Нетрудно увидеть, что практически между всеми возрастными группами каждого региона показатели статистически значимо различаются ( p <  0,02). Однако если сравнение производится в каждой возрастной группе между регионами, то статистически значимых различий нет совсем ( p >  0,05). В то же время объединенные (грубые) показатели смертности по этим же регионам могут парадоксально отличаться почти в три раза (8,92 против 2,67 человека на 1000 населения в год; p <  0,001). Причина артефакта демографам хорошо известна. Она заключается в том, что при объединении страт сыграл роль такой скрытый фактор, как региональное различие распределений жителей по

Таблица 1

Сравнительный анализ показателей смертности среди светлокожих женщин Майами и Аляски в 1970 г.

Возраст, лет	Майами			Аляска
	∆ A , чел.·лет	∆ M (умершие)	Показатель, (‰ в год)	∆ A , чел.·лет	∆ M (умершие)	Показатель, (‰ в год)
< 15	114 350	136	1,19	37 164	59	1,59
15–24	80 259	57	0,71	20 036	18	0,90
25–44	133 440	208	1,56	32 693	37	1,13
45–64	142 670	1 016	7,12	14 947	90	6.02
65 и старше	92 168	3 605	39,11	2 077	81	39,00
Все возрасты*	562 887	5 022	8,92	106 917	285	2,67

Примечание: ^* – crude rate .

возрасту. Объединенная региональная страта оказалась неоднородной. Способ исправления ошибки в данном случае известен. Действительно, можно ввести в рассмотрение любое «стандартное» распределение по возрастным категориям, например, просто объединив две административные единицы в одну. Тогда оценка показателя сведется к подсчету средневзвешенного значения по возрастным группам. Пусть, например, структура распределения долей в едином стандарте дается отношениями 0,23:0,15:0,25:0,23:0,14. Для подгруппы «Майами» показатель составит 7,88 ‰ в год, а в подгруппе «Аляска» – 7,63 ‰ в год. Очевидно, теперь по наблюдаемой разнице уже нельзя сделать заключение о статистически значимых различиях в состоянии здоровья жителей двух регионов. Казалось бы, парадокс преодолен.

Однако сама по себе процедура стандартизации неоднородность не устраняет. Не удивительно, что стандартизированный показатель годового риска уже давно подвергается критике [15], поскольку по его величине все же не удается адекватно судить о состоянии здоровья/нездо-ровья популяции. К этому выводу можно прийти и самостоятельно, например, если сравнить три возрастные зависимости интенсивности смертности от рака легкого для трех разных групп населения, в которых стандартизированный риск был арифметически тождественным (рисунок), зато пожизненный риск различался в 1,25 раза. Причем его значения были выше совсем не в той когорте, где наблюдалась максимальная интенсивность специфической смертности.

Действительно, предположим, что когорты 1 и 2 были подвержены разным уровням воздействия некоторого поллютанта. Фоновая, с нулевым уровнем воздействия когорта используется

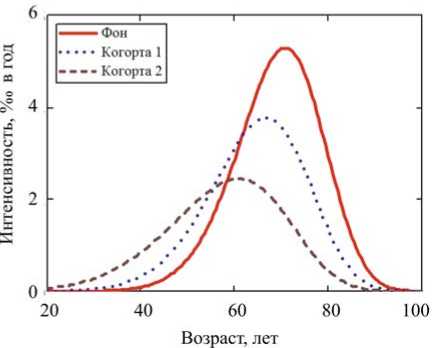
Рис. Возрастная зависимость интенсивности смертности от рака легкого в трех разных когортах мужского пола, обладающих одинаковым стандартизированным показателем 68:100 000 в год. Результат математического моделирования в качестве группы сравнения. Очевидно, если оперировать не категорией стандартизированного показателя риска, а вероятностной категорией ущерба здоровью когорты, то в выборке 2 она будет выше. Это объясняется тем, что регистрация смерти от рака легкого в выборке 2 в аналогичных объемах начнется раньше, что, как можно вычислить, приведет к бόльшей величине кумулятивного эффекта, в качестве которого можно применить пожизненный риск гибели от рака. Таким образом, если откликом на воздействие поллютанта является изменение формы распределения λ(t), то надо правильно выбирать меру биологического эффекта. Она не должна сводиться к «средней температуре по больнице».

Другим примером ошибочного использования годовых показателей риска и пуассоновской регрессии являются работы известной группы исследователей [2, 4, 6–8]. По их наблюдениям, например, уверенно, или статистически значимо, регистрируется снижение заболеваемости артериальной гипертензией вместе с ростом дозы внутреннего облучения на печень свыше 0,05 Гр среди мужчин, контактирующих с соединениями плутония (табл. 2). Между тем доза от плутония 0,05 Гр эквивалентна дозе внешнего облучения 1,0 Зв, что соответствует 50 годам работы на уровне установленного дозового предела допустимого облучения 20 мЗв/год для профессионалов. Таким образом, столь «благоприятное» действие плутония на организм мужчин не находит соответствия действующим нормам радиационной безопасности1. Объяснение этого «феномена» почти такое же, как для табл. 1, однако источников неоднородности страт здесь уже больше, так как выборки составлены из представителей технологически различных производственных участков, причем с двумя совершенно разными видами радиационного облучения. Не помогла даже стандартизация показателя риска, которой авторы работы определенно владели [4]!

Те же исследователи благодаря сравнению неоднородных групп «нашли» не менее парадоксальные результаты. Так, при изучении последствий хронического воздействия ионизирующего излучения на интенсивность смертности от цереброваскулярных заболеваний они «обнаружили», что при альфа-облучении работников мужского пола в дозовом интервале 0,1–0,5 Гр происходил прирост показателя смертности с дозой, а в целом по мужской части когорты «наблюдался» статистически значимый спад с трендом ИОРГр =-0,056 Гр 1 (95%-ный ДИ: от - 0,094 до - 0,018) [8]. До выводов о том, что внутреннее облучение от поступивших в организм радионуклидов было полезным, дело не дошло, но парадокс Симпсона налицо. В другой аналогичной статье на основании проведенных исследований можно обнаружить, что для той же когорты с высоким доверительным уровнем вероятности регулярное употребление алкоголя работниками-мужчинами повышает уровень заболеваемости цереброваскулярными заболеваниями [6]. Для женщин этот показатель, напротив, ниже среди пьющих. И здесь абсурдность и парадокс Симпсона идут рука об руку.

Весьма наглядно несоответствие оценок дозового тренда, наблюдаемое при изучении заболеваемости старческой катарактой, где в основу также положен показатель интенсивности риска возникновения заболевания [2]. Например, в табл. 3 можно видеть, что при однофакторной группировке наблюдений по дозе облучения в основной группе работников, для которых нормы радиационной безопасности² заведомо соблюдались, показатель заболеваемости составил X 0 = 1631/255036 = 6,39 %о • год ^{- 1}. Однако в группе свыше 1 Гр аналогичный показатель составил уже X₄ = 12,31 %о • год ^{- 1}. Тогда избыточный относительный риск на единицу дозы в рамках предположения о линейном тренде должен был бы составить (4):

ИОР_Гр ” —Т⁴--- = 0,89 Гр^-1.   (4)

^Гр X ( D 4 - D 0)          '

Таблица 2

Заболеваемость артериальной гипертензией среди работников ПО «МАЯК», получивших различные дозы внутреннего облучения [4]

Пол	D < 0,025 Гр		0,025–0,05 Гр		D > 0,05 Гр
	Число случаев	Показатель (‰ в год)	Число случаев	Показатель (‰ в год)	Число случаев	Показатель (‰ в год)
Мужчины	1416	21,11 ± 0,5	481	20,65 ± 1,1	963	17,74* ± 0,72
Женщины	694	18,59 ± 0,71	253	21,42 ± 1,68	600	20,61 ± 1,09

Примечание: * – статистически значимое наблюдение.

Таблица 3

Относительный риск (ОР) заболеваемости катарактой в зависимости от кумулятивной дозы внешнего гамма-облучения [2]

Кумулятивная доза внешнего γ-облучения (Гр)	Средняя доза внешнего γ-облучения (Гр)	Человеко-годы наблюдения	Случаи катаракты	ОР (95%-ный ДИ)
(0–0,25)	0,08	255036,0	1631	1
[0,25–0,50)	0,36	69097,1	702	1,23 (1,11–1,35)
[0,50–0,75)	0,62	35678,2	365	1,13 (1,00–1,28)
[0,75–1,00)	0,87	25915,0	321	1,38 (1,21–1,57)
[1,00–1,25)	1,12	18191,8	224	1,43 (1,23–1,66)
[1,25–1,50)	1,37	15147,2	217	1,57 (1,34–1,83)
[1,50–2,00)	1,73	20066,3	296	1,59 (1,39–1,83)
>=2,00	2,67	25498,0	387	1,61 (1,41–1,83)

В области малых доз он еще выше. Однако исследователь Е.В. Брагин и соавт. [2] в своей работе дают иную оценку, сделанную частично с учетом стратификации наблюдений, но по всей когорте, а именно ИОР Гр = 0,28 Гр - 1 (95%-ный ДИ: 0,20–0,37). То есть одна из оценок не попадает в доверительный интервал другой, а сами они различаются примерно в три раза. Парадокс Симпсона налицо. Каким оценкам в этом случае следует доверять? Вероятно, никаким.

В работе Т.В. Азизовой с соавт. [7] попытки раздельного учета влияния двух типов ионизирующей радиации на болезни системы кровообращения (БСК) в рамках раздельного однофакторного анализа также привели к парадоксу. Избыточный относительный риск на единицу дозы при воздействии внешнего гамма-облучения составил 0,05 Гр ^{- 1} (95%-ный ДИ: 0,0-0,11). Был также установлен статистически значимый восходящий тренд смертности от БСК с увеличением поглощенной дозы внутреннего альфа-излучения в печени - ИОР_Гр = 0,27 Гр ^{- 1} (95%-ный ДИ: 0,12–0,48). С учетом относительной биологической эффективности альфа-излучения по сравнению с гамма-излучением получается ИОР Зв = 5,4 Зв ^{- 1} (95%-ный ДИ: 2,4-9,6), что на порядок больше, чем в когорте жертв бомбардировки в Хиросиме и Нагасаки и само по себе должно было вызвать удивление. Но это не помешало авторам написать: «… Результаты … исследования хорошо согласуются с оценками риска, полученными в японской когорте лиц, выживших после атомной бомбардировки …». Стоит отметить, что авторы видели, как «…ИОР_Гр уменьшался и становился статистически незначимым при введении поправки на дозу внешнего гамма-облучения» [2].

В области эпидемиологических исследований действия радиации категория «человеко-годы» используется очень широко. Именно она подталкивает исследователей риска к неоправданным выводам и обобщениям, игнорирующим первоначальный вероятностный смысл введения показателей. Имеется существенный методологический дефект, когда с целью оценки риска смерти в радиационно-эпидемиологических исследованиях измеряется показатель hazard, но не сам риск. Логическое противоречие особенно типично при изучении стохастических событий в когорте. Они обычно зависят от дозы воздействия D, которая кумулятивна по своему смыслу, в то время как показатель риска λ(t) является «мгновенной» характеристикой когорты, которую можно отнести к некоторому возрасту. Однозначная связь λ(t) с дозой кажется логичной для острого воздействия вредного вещества, но совершенно не характерна для пролонгированного действия. Например, хроническое низкоинтенсивное радиационное облучение предполагает корреляцию дозы и возраста. Если обычная для эпидемиологии стратификация производится по обеим этим величинам, то при низких уровнях облучения будет естественным, что для лиц со сравнительно бόльшими возрастами смерти наблюдаемая доза окажется больше. Применение методов максимального правдоподобия по типу руководства Epicure Users Guide [23] приведет к ложной интерпретации этого факта: для членов когорты с бόльшей дозой регистрируемая продолжительность жизни окажется выше, а «мгновенные» показатели специфической смертности λ(t, D) – ниже. Таким образом, применение показателя интенсивности смертности/заболеваемости чревато эпидемиологическим «наблюдением» лож- ного гормезиса, что на самом деле могло бы являться не более чем математическим артефактом. Несмотря на использование сослагательного наклонения в предыдущем предложении, автор уверен, что отмеченный артефакт неоднократно наблюдался в области малых доз, где он очевидным образом должен быть выражен более всего. При этом подобное явление многими исследователями трактовалось как истинный радиационно-эпидемиологический гормезис или даже антиопухолевый эффект [10–16, 18–22, 24, 25].

Обсуждение и анализ проблемы оценки риска. Знание и нормирование основных факторов риска лежит в основе государственного санитарно-эпидемиологического контроля и регулирования. Но любая наука, построенная на опыте, нуждается в своем особом инструментарии. Недостаточно определить понятие риска теоретически. Его необходимо также уметь измерять на практике. Риск всегда обусловлен несколькими внешними и внутренними причинами, то есть является многофакторной величиной. Обеспечить строго однофакторную зависимость риска можно только в эксперименте, который по этическим причинам не всегда может быть выполнен на людях. Альтернативой являются эпидемиологические или клинико-эпидемиологические исследования многофакторного типа. Без получения такой информации невозможна практика управления рисками, требующая умения их прогнозировать в заданных санитарно-эпидемиологических условиях.

Анализ сложившейся практики оценки рисков показывает, что традиционно используемые таблицы сопряженности или однофакторные статистические инструменты трудно приспособить к многофакторным рандомизированным наблюдениям. Как было показано выше, пуассоновская регрессия, построенная на ошибочном использовании категории человеко-лет наблюдения, может приводить к ложным выводам. Одним из вариантов решения проблемы может быть переход к оценке сугубо вероятностных показателей специфического риска, например, условного пожизненного риска. В области радиационной эпидемиологии имеется положительный пример – к нему прямо призывает Международная комиссия по радиологической защите (МКРЗ) [5].

Алгоритм статистического исследования, построенный на принципе оценки кумулятив- ного эффекта, может использоваться и при анализе нерадиационных воздействий, если только их величину можно будет характеризовать некими кумулятивными «дозами». Риск может быть только условным, а значит, будет зависеть от пола, момента начала экспозиции, момента наблюдения индивидуального эффекта в группе, от сопутствующих физиологических процессов, способных повлиять на наблюдаемый маркер эффекта, от статуса курения, от локализации ущерба, от характера воздействия. Фактором, вызывающим неоднородность выборки, может являться даже способ наблюдения биологического эффекта (способ постановки диагноза). Недаром в среде эпидемиологов используется термин «выявляемость». Наконец, исследуемый риск отдаленных последствий зависит от возможности реализации иных смертельных рисков. Все эти факторы являются условиями для реализации условной вероятности, а значит, должны являться условиями и для ее оценки.

Выводы. Оценка пожизненного риска и его дозового тренда в любой неоднородной когорте является сложной статистической проблемой многофакторного анализа, решить которую без специализированных вычислительных средств невозможно. Доступное в настоящее время универсальное программное обеспечение, как правило, слабо пригодно для этой цели. Необходимо создание специализированного программного обеспечения, способного решать задачу оценки рисков как обратную. Прототипом могла бы послужить логистическая регрессия, если только не абсолютизировать роль логистической функции, вместо которой следовало бы использовать более гибкий инструмент аппроксимации. Например, в качестве генератора моделей связи риска с изучаемыми факторами можно применять искусственные нейронные сети. Это позволило бы, в частности, совсем отказаться от идеи стратификации результатов рандомизированных наблюдений и, следовательно, исключить известное влияние назначения границ страт на результаты оценки. Областей приложения в медицине и здравоохранении имеется много – прогнозирование по результатам скрининга (онкология, кардиология, гастроэнтерология и др.), медицинская статистика, когортная и клиническая эпидемиология, клиническая токсикология, а также создание программного обеспечения обработки иной статистической информации, показатели которой имеют вероятностный характер.