Острая фокусировка лазерного света путем резонансного возбуждения в однородном диэлектрическом микроцилиндре

В последнее время внимание уделяется изучению субволновой фокусировки лазерного света на микрочастицах, в том числе на микросферах и микроцилиндрах, радиусы которых сравнимы с длиной волны падающего света [1-5]. Так в [1-4] численно исследовалась фокусировка многослойными микросферами [1], сфероидальными микросферами [2], двухслойными микросферами [3, 4]. Минимальный диаметр фокусного пятна по полуспаду интенсивности среди рассмотренных работ FWHM=0,4 X, где X - длина волны [2], а максимальная протяженность пятна по полуспаду вдоль оптической оси (глубина фокуса) DOF=20 X [3, 4]. В [5,6] рассматривалась фокусировка микроцилидром: эллиптическим[5] и многослойным[6]. Минимальная ширина по полуспаду FWHM=0,46 X была получена в [6]. В [7,8] моделировалась резонансное возбуждение моды шепчущей галереи в диэлектрической микросфере. В [7] с помощью диэлектрической микросферы с нанометровым металлическим шариком получено фокусное пятно с шириной FWHM=0,25 X , для диэлектрической микросферы было получено при помощи резонансного возбуждения фокусное пятно с шириной FWHM=0,4 X [8].

В данной статье рассматривается фокусировка TE-поляризованного лазерного света микроцилиндром. Для 19-ой моды (мода шепчущей галереи) получено фокусное пятно с шириной FWHM=0,22 X вне цилиндра. Это меньше, чем во всех перечисленных работах.

РЕЗОНАНСНОЕ ВОЗБУЖДЕНИЕ

Из аналитического решения задачи дифракции гауссова ТЕ-поляризованного пучка на однородном диэлектрическом цилиндре могут быть найдены решения, соответствующие резонансным возбуждениям — то есть случаям, когда в цилиндре происходит усиление одной из мод Бесселя. Поле внутри цилиндра выражается в виде ряда [9]:

E_m ( r , Ф ) = Е i^jb j C j J j (.knr ) e i * , (1)

где k — волновое число в вакууме; n — показатель преломления света в среде; (r, ф ) — полярные координаты в плоскости сечения цилиндра; b_j — коэффициент разложения, зависящий от геометрии, а C_j — коэффициент, зависящий от конфигурации падающего поля. Коэффициенты определяются формулами

C = Ю0 П exp | - q Ю° - ik(px0 + qy0) - ij arcsin q | dq (2) j M A 4      0 0        J b = Jj( kR) H jiy (kR) - J‘(kR) H «(kR)

j   Jj( nkR) H jiy (kR) - nJ' (nkR) H j1)( kR) , где, соответственно, ю0 — радиус перетяжки гауссова пучка, (x0, y0) — положение перетяжки в декартовых координатах, R — радиус цилиндра, p = ^ 1 -q2 . Можно отметить, что: во-первых, при значениях знаменателя bj близких к нулю можно получить усиление в (1) той или иной Бесселевой моды, а во-вторых, эффект зави- сит только от длины волны падающего света, так как bj не зависит от положения и радиуса перетяжки.

ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ

Резонанс был исследован на диэлектрическом цилиндре с показателем n = 1,59. Был подобран радиус цилиндра, при котором возникает увеличение коэффициента при 19 моде Бесселя. Цилиндра с радиусом R = 2,175 X облучался гауссовым пучком с радиусом ю₀ = 19 X, перетяжка которого располагается на расстоянии 3 X от оси цилиндра. Для анализа было получено по точкам распределение на рис. 1. Значения напряженности для распределения были посчитаны по первым 100 слагаемым (первые 50 для положительных индексов и 50 для отрицательных в (1)) с шагом 1/20 X . Интенсивность рассчитывалась как квадрат модуля напряженности. В рассматриваемом случае свет фокусируется в пятно с DOF = 0,25 X и FWHM = 0,2 X , что более чем в два раза меньше дифракционного предела в воздухе для двумерного случая (FWHM = 0,44 X ). Интенсивность света в точке максимума в п = 48,9 раз превосходит интенсивность падающего гауссова пучка в перетяжке.

Полученная картина интенсивности неустойчива, и при малом отклонении радиуса от установленного значения максимумы на границе цилиндра пропадают. На рис. 2 представлена зависимость отношения значения интенсивности в точке максимума к интенсивности гауссова пучка в перетяжке п . На рисунке пикам соответствуют случаи резонансного возбуждения бесселевых мод. Указанному радиусу 2,175 X соответствует 19 мода, а первому максимуму на графике — 9 мода ( R = 1,05 X ). Ширина максимума для 19 моды составляет 0,003 X .

Кривая для глубины фокуса DOF представлена на рис. 3. Следует отметить, что минимумам на кривой соответствуют максимумы на кривой рис. 2, то есть резонансное возбуждение всегда сопровождается уменьшение размеров фокусного пятна. FHWM при резонансном возбуждении уменьшается до 0,2 X .

При фокусировке цилиндром с R = 2,2 X образуется пятно с DOF = 0,8 X и FWHM = 0,4 X .

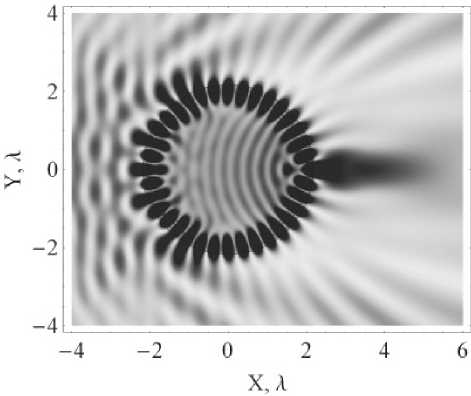
Рис. 1. Негативное распределение интенсивности в сечении цилиндра для случая резонанса

Интенсивность в максимуме превосходит интенсивность в перетяжке в 8,8 раз. Отношение значений интегралов интенсивности по области фокусного пятна (энергетических эффективностей) в резонансном и нерезонансном случае можно оценить отношением произведения DOF, FWHM и п . Для R = 2,175 X и R = 2,2 X отношение отказывается приближенно равным 0,86. Это соответствует потере 14 процентов в энергетической эффективности фокусировки, однако в то же время это указывает на лучшую локализацию энергии при резонансном возбуждении — при уменьшении области фокуса в 6,4 раз эффективность падает всего на 14 процентов. Не исключается возможность сохранения энергетической эффективности, однако это должно означать, что интенсивность в максимуме выше, чем указанное выше, так как точку максимума не удалось точно определить из-за дискретизации распределений.

ЗАКЛЮЧЕНИЕ

В работе численно, на основе аналитического решения уравнений Максвелла, показано, что из решения задачи дифракции монохроматического

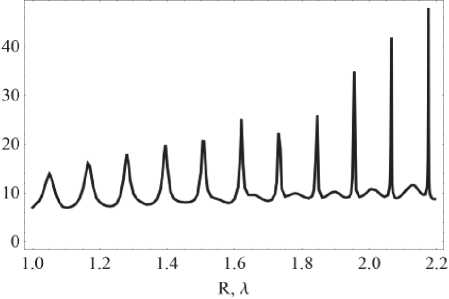
Рис. 2. Отношение интенсивностей п в точке максимума и перетяжке гауссова пучка для различных радиусов цилиндра

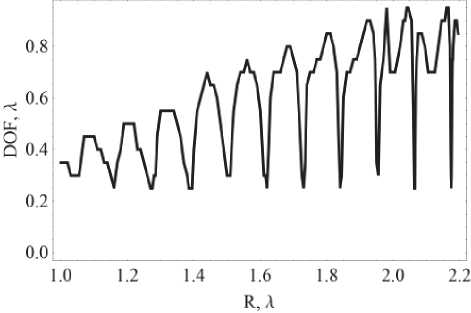
Рис. 3. Зависимость глубины фокуса от радиуса цилиндра

непараксиального гауссова пучка на однородном диэлектрическом цилиндре при радиусах цилиндра, сравнимых с длиной волны света, можно получить фокусное пятно вне цилиндра, размер которого в два раза меньше дифракционного предела. Для рассмотренного решения можно отметить, что в разложении по функциям Бесселя напряженности поля, коэффициент при 19 моде превосходит все остальные. На распределениях это выражается в периодических максимумах вблизи границ цилиндра.