Отражение крутильной бегущей волны в стержне с искусственным дефектом

1.    Постановка задачи

В колонне бурильных труб не все участки могут быть доступны для визуального осмотра и приборного диагностирования. В настоящей работе предлагается методика диагностирования длинных стержней с помощью измерений величин параметров крутильных бегущих волн. В случае стержней конечной длины наличие в них дефектов может быть диагностировано по изменению спектра собственных изгибных, продольных или крутильных колебаний [1–11]. В [1] по известной зависимости перемещения свободного конца стержня от частоты возмущающей силы находится переменная площадь поперечного сечения стержня как функция продольной координаты. В статьях [2–3] исследуются обратные задачи теории трещин в твердых телах. Вычисление массы, скорости движения груза и положение места его удара по стержню исходя из анализа продольных смещений одного из сечений стержня выполнено в [4]. Решению обратных задач о продольных волнах в стержнях конечной длины посвящены работы [5, 6]. В [7] поставлена обратная задача для определения начальной координаты и размера поперечного надреза вала турбокомпрессора по трем собственным частотам крутильных колебаний. В [8] и ряде других работ трещина в стержне моделируется пружиной, а повреждение балки, совершающей изгибные колебания — вращательной пружиной. Обзор таких исследований имеется в [9]. В [10] предложено решение обратной задачи, позволяющее найти координату повреждения стержня и параметр, содержащий его глубину и длину, по характеристикам продольной падающей и отраженной волн в месте наблюдения.

В данной работе рассматривается установившийся процесс отражения от надреза и прохождения крутильной бегущей волны, распространяющейся по бесконечному стержню с полярным моментом инерции поперечного сечения Jp . В точке с координатой xc стержень имеет поперечный надрез длиной l и полярный момент инерции поперечного сечения в этом месте jp (Рис. 1) Предполагается, что поперечный размер стержня и длина надреза l значительно меньше длины волны λ . Не учитываются затухание колебаний в стержне и пространственный характер напряженно-деформированного состояния в зоне надреза. В такой постановке определяются

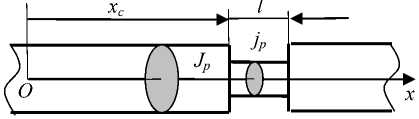
Рис. 1. Расчетная схема

отраженная и проходящая волны по известным параметрам надреза и его координате (прямая задача). Определение координат надреза и его размеров по отраженной волне в точке наблюдения представляет собой обратную задачу.

Дифференциальное уравнение крутильных колебаний стержня имеет вид [11]:

д 2 ф - £ .д ф = 0 c 2 = G д x ² G д t ²              p

где ф — угловое перемещение элемента стержня; c — скорость распространения волны сдвига; G , ρ — модуль сдвига и плотность материала стержня; x — продольная координата на оси, берущей начало в точке наблюдения и совпадающей с осью стержня; t — время. В решаемой задаче угловые перемещения возбуждаются источником, находящимся на расстоянии x = -» , и представляют собой в (1) бегущую волну ф = Ф sin ( ю t - kx ) , где Ф, ю — амплитуда и частота крутильной волны, к — волновое число к = ю/ c . Вводя параметр X = 2п с /ю и переходя к безразмерным переменным q = 2nx /X, q c = 2nx c /X, т = ю t , ф = ф/Ф, e = 2п l /X, падающую и отраженную волны представим в виде:

– до области надреза

	ф = sin ( т - q ) , -*< q < q c , ф 1 = A 1 cos ( т+q ) + B 1 sin ( т+q ) , -»< q < q c ;                              (2)
– для области надреза:	ф 2 = A 2 cos ( т - q ) + B 2 sin ( т - q ) , q c <  q <  q c + e ,                             (3) ф3 = A 3 cos ( т+q ) + b 3 sin ( т+q ) , q c <  q <  q c + e.

За областью надреза проходящая волна имеет вид:

ф4 = A4 cos(т-q) + B4 sin(т-q), qc + е < q <м.(4)

На краях надреза запишем условия равенства угловых перемещений и крутящих моментов:

m = Jp",   q = q c , jp q = q c + e

д(ф+ф1) а(ф2 + фз) ф+ф1 = ф2+ фз,   m   ..—=, — dqd

^д( ф 2 + ф з )

ф2 + фз = ф4 ,       ,---- = m —, dq

• 2.    Прямая задача

Из условий (5), (6) получаем коэффициенты выражений (2)–(4):

gA = |^2m (m2 -1) cos 2^c -(m4 -1) tge sin2qc J tge, gB1 = [(m4 -1)tge cos2^c + 2m(m2 -1)sin2qc J tge, gA2 = -m(m2 -1)(m-1)tge,   gB2 = m(m +1)^2m + (m2 +1)tg2eJ, gA3 = m (m -1){(m2 +1) tge cos2qc + |^2m -(m2 +1) tg2e J sin2qc},                     (7)

gB3 = m(m -1){[(m2 +1)tg2e - 2mJ cos2qc +(m2 +1)tge sin2qc}, gA4 = -2 m (m -1)2 tge,   gB4 = 2 m |^2 m + (m2 +1) tg 2e J.

Отраженную от надреза (2) и проходящую через надрез (4) волны можно также представить как

ф1 = k1sin (т + q - По), ф4 = к4 sin (т - q - V), -»< q < qc,                              (8) qc + e < q < m,                                (9) где коэффициенты отражения к1 и прохождения к4 и соответствующие фазы п0 и ^ находятся по формулам к           (1 - m2) sin s k1 — /                                     ,     k4 — /,

( m ² + 1 ) - ( m ² - 1 ) cos ² s           ( mm ² + 1 ) - ( m ² - 1 ) cos ² s

-2m cos s cos 2^c +(m2 +1) sinesin2cc              (m -1)2 tge gn0 —                                            , tgV —

( m ² + 1 ) sine cos 2 c _c + 2 m cosesin2 ^ _c           2 m + ( m ² + 1 ) tg ² e

Сдвиг фазы между падающей и отраженной волной η в точке с координатой ξ определяется выражением: П ^— П о ^- 2£

Из соотношений (7)–(10) видно, что коэффициенты отражения и прохождения, а также сдвиг фазы между падающей и проходящей волной ψ зависят только от относительных параметров надреза m и ε . Сдвиг фазы между падающей и отраженной волной η зависит как от параметров m и ε , так и от положения надреза ^_c и координаты места проведения замеров ^ . При отсутствии надреза ( m ^ 1) из (10) следует, что к 1 ^ 0, к ₄ ^ 1.

Суммарные угловые перемещения элемента стержня Λ в точке наблюдения ( ξ=0) состоят из перемещений, вызванных отраженной и падающей волнами:

Л —ф + ф 1 — C sin ( т-5 ) .                                    (11)

Здесь амплитуда суммарного углового перемещения С и сдвиг фазы суммарной волны δ вычисляются с помощью формул:

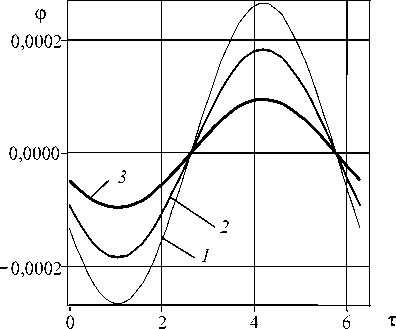
Рис. 2. Зависимости от т углового перемещения элемента стержня в точке наблюдения ^ = 0 в отраженной волне для

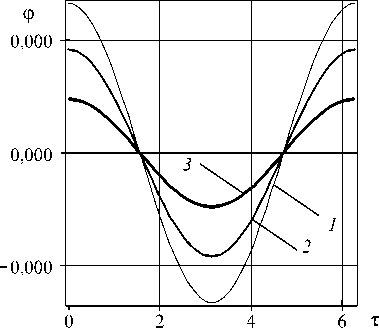
двух положений надреза: £ _с = 2 п/ 3 ( а ), ^ c = 2 п ( б ) при £ = 0,001 и различных значениях m : 1,1 (кривые 1 ); 1,2 ( 2 ); 1,3 ( 3 )

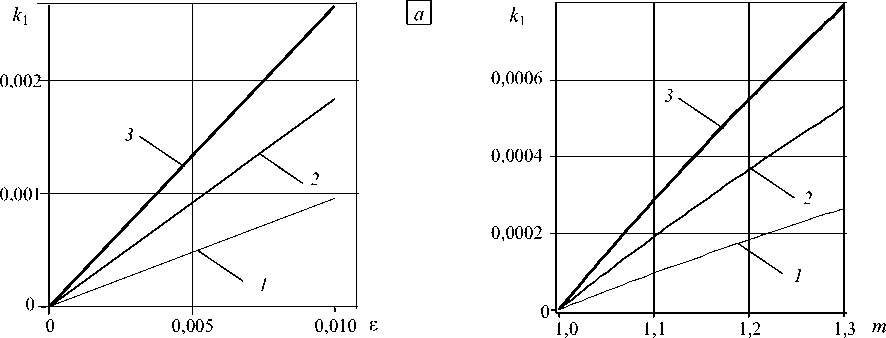
Рис. 3. Зависимости коэффициента отражения k j от £ ( а ) при различных значениях m : 1,1 (кривая 1 ); 1,2 ( 2 ); 1,3 ( 3 ),

б

и от m ( б ) при различных значениях £ : 0,001 (кривая 1 ); 0,002 ( 2 ); 0,003 ( 3 )

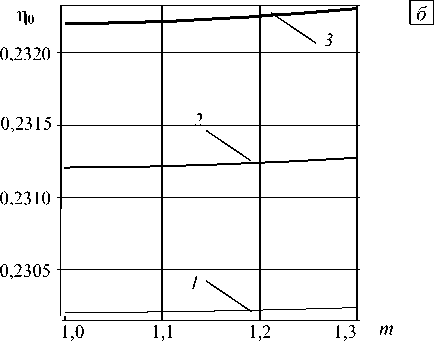
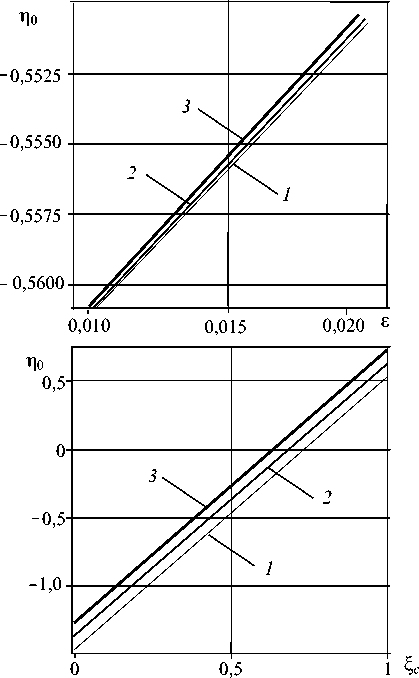
Рис. 4. Сдвиг фазы в отраженной волне П е в зависимости от £ ( а ) при £ _с = 0,5 и различных значениях параметра m : 1,1 (кривая 1 ); 1,2 ( 2 ); 1,3 ( 3 ); от параметра m ( б ) при различных значениях £ : 0,001 (кривая 1 ); 0,002 ( 2 ); 0,003 ( 3 ); от положения надреза ^ _с ( в ) при различных значениях £ : 0,001 (кривая 1 ); 0,002 ( 2 ); 0,003 ( 3 )

в области их малых значений, то есть в случае небольшого надреза. Причем на коэффициент отражения k ₁ не влияет координата надреза ^ _c , что является следствием пренебрежения эффектами затухания в стержне. Сдвиг фазы в отраженной волне п₀ в зависимости от параметров б , m и положения надреза ^ _c содержит рисунок 4. Анализ кривых указывает на периодическую зависимость сдвига фазы в отраженной волне. Таким образом, сдвиг фазы в отраженной волне можно использовать для определения координаты надреза или зарождающегося повреждения.

3.    Обратная задача

Способы определения параметров надреза в стержне по измеряемым с помощью приборных средств характеристикам отраженной и проходящей волн подробно описываются в работе [12].

При m = 1,5; ^ _c = 0,9; б = 0,0001, полученных на основе замеренных параметров надреза, вычисленные значения коэффициентов в решении прямой задачи (7) получаются равными: A 1 =- 0,000009471149704; B 1 = 0,00004057595872; A ₄ =- 0,000008333333254. Следует заметить, что A 1 = ф 1 ( 0; 0 ) , B 1 = ф 1 ( л/ 2; 0 ) , A ₄ = ф ₄ ( 2 п ; 2 п ) . Значения остальных коэффициентов здесь не приводятся.

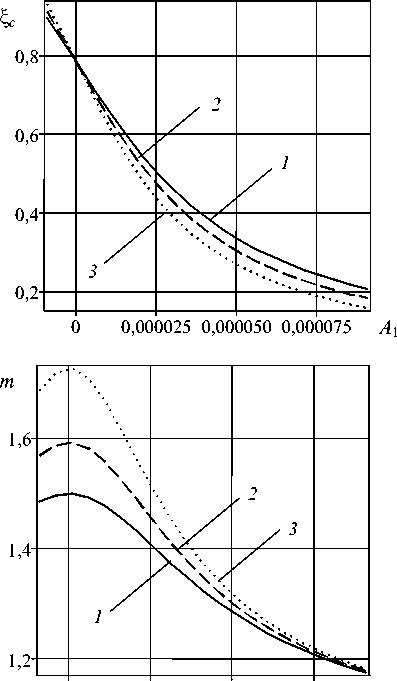
В случае замера характеристик отраженной и проходящей волн A 1 = - 0,000009, B 1 = 0,00004 , A ₄ =- 0,000008 решение обратной задачи дает значения параметров: m = 1,484848488 , ^ _c = 0,8960008533, б = 0,0001010624996. На рисунке 5 приводятся зависимости относительной координаты ^ _c и длины надреза б и параметра m от A 1 при различных значениях B 1 и фиксированном A ₄ =- 0,000008 . Таким образом, трех замеренных величин ( A ₁, B ₁ , A ₄) оказывается достаточно для того, чтобы установить размер дефекта и его местоположение.

Возможно использование и других замеренных параметров падающей, отраженной от надреза и проходящей волн. Требования повышенной точности измерений с помощью приборных средств и применения регуляризации в обратной задаче являются обычными и здесь не обсуждаются.

а

в

0,000025 0,000050 0,000075    A 1

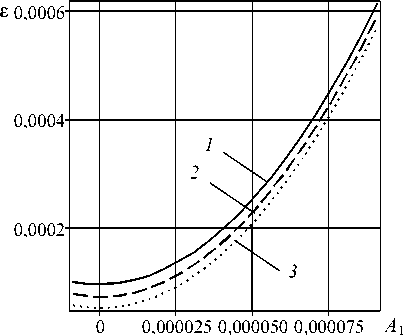
Рис. 5. Зависимости координаты надреза ^_c ( а ), его длины б ( б ) и параметра m ( в ) от A 1 при A ₄ =- 0,000008 и различных значениях B 1 : 0.00004 (кривая 1 ); 0.000035 ( 2 ); 0.00003 ( 3 )

4.    Частные случаи

Далее приводится несколько вариантов повреждений стержня и соответствующие характеристики отраженной, проходящей и суммарной волн.

• 1.    Повреждение стержня при с = с c отсутствует. Тогда: m = 1, к 1 = 0, n ₀ = - 2 £ c , к 4 = 1, V = 0, C = 1, 5 = 0.

• 2.    Имеется небольшое повреждение стержня ( m >  1) или его утолщение ( m <  1) при ^ = ^ c . В этом случае:

• 3.    Обрыв стержня при с = c c . Здесь m ^ « , k 1 = 1, n ₀ = 2 ^ c , к ₄ = 0, V = 0, C = 1, 5 = ^ _c .

• 4.    В точке ξ=ξ c  на стержень надето специальное приспособление, фиксирующее его угловое

m ^ 1, к1 = (m2 - 1)б/2m, п0 = 2^c — п/2, к4 = 1 -(m -1)m )2 б2/8, V = 2^c -л/2,

C = 1 + ( m - 1) m ) б sin2 ^ c /2, tg 5 = ( m - 1/m ) б cos2 ^ c /2.

перемещение. Тогда: m = 0, k 1 = 1, n ₀ = 2 ^ _c , к ₄ = 0, V = 0, C = 2 sin ^ _c , 5 = ^ _c .

Анализ отраженных и суммарных волн в стержне позволяет сделать вывод о том, что амплитуда и сдвиг фазы обуславливаются величиной и положением надреза. Изменение сдвига фазы в отраженной волне от положения надреза ^ c имеет периодический характер. В то же время сдвиг фазы практически не зависит от длины надреза б и параметра m .

Поскольку по сдвигу фазы в отраженной волне можно определить координату надреза или зарождающегося повреждения, полученная методика может быть применена для разработки системы диагностирования повреждений длинных стержневых систем.

Работа выполнена при финансовой поддержке РФФИ (проект № 11-01-00293_а).