Отражение продольной волны от надреза в стержне, погруженном в вязкую жидкость

от частоты возмущающей силы. Решению обратной задачи о продольных установившихся колебаниях в стержнях с повреждением посвящена работа [5]. В [6] рассматривается отражение продольной бегущей волны в стержне с повреждением без учета затухания волн.

1. Постановка задачи

Предполагается, что из удаленной точки стержня круглого поперечного сечения радиусом R слева направо распространяется продольная волна смещения, амплитуда и частота которой в точке наблюдения O с координатой x = 0 равны U и ω. Стержень при этом находится в вязкой несжимаемой жидкости. В точке с координатой x c имеется надрез длиной l (Рис. 1). Длина надреза l значительно меньше длины волны L. В пределах надреза с короткой длиной l и вблизи него имеется сложное пространственное напряженно-деформированное состояние. Однако здесь для простоты принимаем одноосное растяжение–сжатие. Требуется определить отраженную и проходящую волны по известным параметрам надреза, а также расположение надреза и его размеры по отраженной волне в точке наблюдения или по отраженной и проходящей волнам.

xc

l

Рис. 1. Расчетная схема

x

n R ²

Между напряжением с и деформацией 8 примем следующую зависимость:

„f      д8 )         ди

с = EI 8 + Ц-- I,    8 =---,

V      дt )         дx где E, ц — модуль упругости и коэффициент внутреннего трения, и — перемещение, t — время.

Поведение жидкости определяется условием на поверхности соприкосновения

vx = д и] д t (r = R)

и условием несжимаемости

д(rvx ) + д(rvr ) = 0 дx       д r      '

где vx, vr — скорости жидкости в продольном и радиальном направлениях. Касательное напряжение в продольном направлении равно f д vx   д vr )

т = ц l I — - + — r - I.

V д r   дx )

Здесь цl — динамический коэффициент вязкости жидкости. Ввиду малости vr по сравнению с vx и их соответствующих первых производных при продольных колебаниях стержня вторые члены в соотношениях (3), (4) далее опускаем. Тогда vx = Vr 1,       т = цlVr 2.

Величина V = Rдu / дt определяется по формуле (2). На поверхность стержня действует напряжение ц, ди т = —---

.

R д t

Из уравнения продольного движения стержня

2 до        д2и „ „ пR 2 — = пR 2р —- + 2 пR т дx         д t 2

и соотношений (1) и (5) следует:

д ² и a t²"

д ² и      ₂

—:— p a д x ²

д ³ и д x ² д t

к ди а + b— = 0, д t

2 E a = —, ^ρ

b = 2^ , R 2 ρ

₂⁽д и      б ² и

T = п RE — + p-- , д x      д x д t ,

где р , a, T — плотность, скорость звука и усилие натяжения в стержне, b — коэффициент влияния жидкости на продольное движение стержня.

В пределах надреза и вблизи него имеется сложное осесимметричное напряженно-деформированное состояние. Однако здесь для простоты принимаем, что имеет место одноосное растяжение-сжатие; сохраняется соотношение о ( а ) в виде (1). Обозначая функции индексами «1», «2», «3», соответственно, в областях - да <  x <  x c , x c <  x <  x c + 1 , x c + 1 <  x <  да, запишем условия стыкования решений при x = x c и x = x c + 1 :

и 1 = и ₂,     T 1 = T ₂,     ( x = x c ) ,

и ₂ = и ₃,     T ₂ = T ₃,     ( x = x c + 1 ) .

Условия вида (7) приводятся также в статье [7], где предложена универсальная процедура обработки данных разрезного стержня Гопкинсона [8]. Условия (7) с учетом (6) записываются в виде ди,     д2 и и, = и., —1 + p---2

^{1    2}     д x     д x д t

⁽ ди , = m —² + p . д x

д ² и ₂

д x д t ’

и ₂ = и ₃,

д и7     д2 и, m —- + p--2

. д x      д x д t

д и, . д² и,      ,         . a               f

= —3 + p---3,   (x = x +1),   m = —7, дx     дx д t    V c )         nR2

где f — площадь поперечного сечения стержня в зоне надреза. Таким образом, в приведенной простейшей модели надреза фигурируют его координата xc, длина l и безразмерный параметр m. В прямой задаче значения xc, l, m (или отношениe площадей f /nR2 задаются. В обратной задаче значения xc, l и параметра m необходимо определять.

Продольное перемещение в стержне без надреза задается в виде затухающей бегущей волны

u — Ue ^e x sin ( и t - ax ) ,                                                                   (9)

где α и β определяются из уравнений, вытекающих из (6):

to² + a ²p² — a ²a² — 2p a ²аРи — 0, a ² ( 2aP + pиp² — proa² ) — b to — 0.

Решение уравнений (10) имеет вид

to (b+pto )        z, a 2 a (1 + p 2и2) z’ P a ’

где z_i — корни уравнения

4 ( 1 + p²и² ) z 4 +4и² ( 1 — p b + p²и² — p³ b и² ) z ² — и² ( b ² + 2p b и² + p²и⁴ ) — 0,

которые равны

z — ±.

±

и ( J p² b ²и² + и² + b ² + p ²и⁴ + p b - 1 )

2 ( 1 + p ²и² )

Во многих случаях возможно пренебрежение величинами порядка ( рю )² и b ², малыми по сравнению с единицей. Тогда из (11) следует:

ω 1₂              2π a

— —,    в — —( pи + b ) ,    L — ---.                                        (12)

a 2 a                ω

В таком приближении длина волны не зависит от затухания в системе.

2. Прямая задача

Пользуясь в дальнейшем обозначениями

2πx    2πx    2πlβLu t — и t,   ^ —---, L —----, а —---, n — —, u — —,

L^cLL 2π   ⁱU

представим (9) в виде

u i = e - n § sin ( t* - § ) ,     -да< § <  § c .

Решение уравнения (6) имеет вид:

u r 1 = e - n ⁽ § c "^У [ A r 1 cos ( t * + § ) + B r 1 sin ( t * + § ) ]

u t i = e" n§ [ A t i^cos ( t* ^- § )⁺ B t i ^sin ( t* ^- § ) ]

ur2 = e~n(§c+E-§) [ Ar2 cos (t* + §) + Br2 sin (t* + § ) J ut2 = e-n(§-§c-E) [ At2 cos (t* - §) + Bt2 sin (t* - § ) J для области - да < ^ < ^,        (14)

для области £c < £ < £c + £, для области ^c + £ < ^ < да.        (17)

Так как при £ = £c выполняются равенства и 1 = ui + ur 1, u2 = u,2 + ut 1, а при £ = ^c + £ — равенства u2 = ur2 + ut 1, u3 = ut2, то с учетом соотношений sin (§c + £ )* sin §c + £ cos §c,    cos (§c + £ )* cos §c - £ sin §c из условий (8) следует:

• A , 1 = ( m 2 - 1 ) £П [ ( m ²£ + 2 mn + £ ) sin2§ _c + 2 m ( 2 n £ - 1 ) cos2§ _c J , B r ₁ =- ( m ² - 1 ) £n | 2 m ( 2 n£ + 1 ) sin2§ _c + ( m ²£ + 2 mn + £ ) cos2§ _c J ,

  
  

A t ₂ = 2 m £n ( 1 - m ) 2 ( 3 n £ - 1 ) ,

Bt2 =-2mn(4mn£ - m2£2 -m2n£ - 2m -n£ - £2), где

П = e ⁿ § ^c

( 4 m 2 +4 mn £ ( 1 - m ) 2

+ £2 (1 + m2) )

Здесь сохранены члены, содержащие £ ² и n ², но не учтены величины n ² £ ², малые по сравнению с единицей.

Решения (14), (17) можно представить также в виде ur 1 = kr 1 e-n(§c-§) sin (( t* + § ) - фr 1 ) ,    - ” < § < §c ,

ut 2 = kt 2 e - n § sin (( t *- § )-Ф 12 ) , § c + £ < § <”, где kr 1 и kt2 — коэффициенты отражения и прохождения, фr 1 и ф12 — соответствующие фазы:

к, 1 = 4 A;1+B;,,   к, 2 = AA+B^, ф r 1 = arctg (-Br 1/Ar 1 ) ,    ф 12 = arctg (-Bt 2/At 2 ) .

При 8^ 0 коэффициент отражения k r 1 ^ 0, а коэффициент прохождения k t 2 ^ exp( - n ^ с ). При обрыве стержня m ^ 0 и коэффициенты равны: k r 1 = exp( - n ^ _c ), k t 2 = 0. Случай, когда n = 0 рассмотрен авторами в работе [6].

Суммарное перемещение us элемента стержня в точке наблюдения (^ = 0), выраженное через амплитуду С и фазу δ волны, имеет вид us = ui+ ur 1 = C sin (t *- 6),   C = 4 C + C22,   tg6 = - C1/ C2,                      (21)

где обозначено

C 1 = ( m ² - 1 ) an ( ( m 2 c + 2 mn + 8 ) sin 2^ _c + 2 m ( 2 n 8 - 1 ) cos 2^ _c ) ,

C ₂ = 1 - ( m ² - 1 ) an ( 2 m ( 2 n 8 + 1 ) sin 2^ _c + ( m 2 8 + 2 mn + 8 ) cos 2^ _c ) .

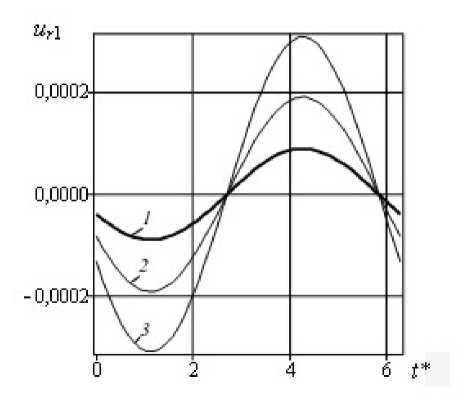
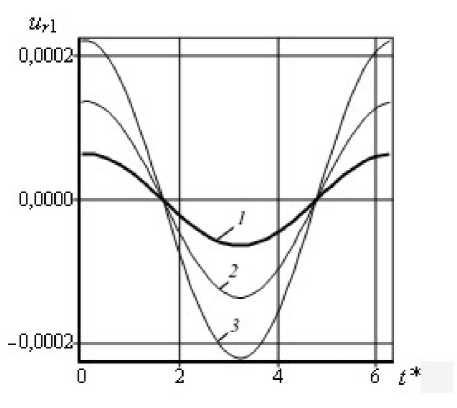
На рисунке 2 приводятся зависимости перемещения элемента стержня в отраженной волне от безразмерного времени t при n = 0,08, 8 = 0,001, ^ = 0 и различных m , вычисленные по формуле u r 1 = k r 1 exp( - n ^ _c )sin( t *- ф r 1 ), для двух значений положения надреза ^ _c . Видно, что отраженные волны зависят от параметра m и координаты надреза. Чем больше отношение площадей m , тем меньше величина сигнала в отраженной волне.

Зависимости сдвига фазы в отраженной волне при n = 0,08 от положения надреза ^ _c и различных значений параметра m представлены на рисунке 3, а , а от параметра m и различных значений ^ _c даются на рисунке 3, б . Анализ графиков показывает, что сдвиг фазы в отраженной волне обуславливается положением надреза ^ _c периодическим образом, а длина надреза 8 и параметр m практически не влияют на сдвиг фазы. Таким образом, сдвиг фазы в отраженной волне можно использовать для определения координаты надреза или зарождающегося повреждения.

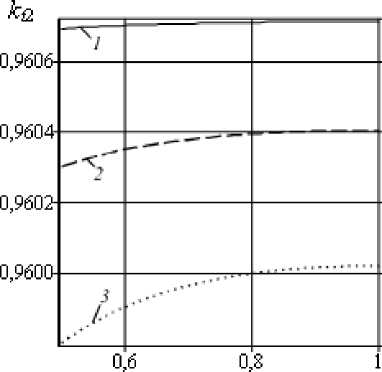
Рисунок 4 содержит зависимости коэффициентов отражения k r 1 и прохождения k t 2 от параметра m . Фрагменты а и в соответствуют различным n (0; 0,04; 0,08) и длине надреза 8 = 0,001, фрагменты б и г — различным длинам надреза 8 (0,001; 0,005; 0,010) при n = 0,08. С ростом параметра m происходит уменьшение коэффициента отражения k r 1 и увеличение коэффициента прохождения k t 2 .

а                                         б

Рис. 2. Перемещения стержня в отраженной волне для положений надреза ^ _c = 2 п /3 ( а ), ^ _c = 2п ( б ) при различных m : 0,9 (кривая 1 ); 0,8 ( 2 ); 0,7 ( 3 )

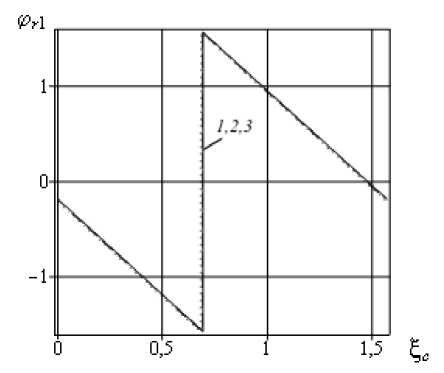
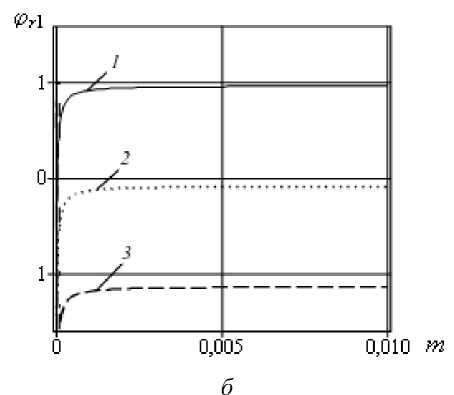
Рис. 3. Зависимости сдвига фазы в отраженной волне от положения надреза ^ c ( а ) при значениях параметра m : 0,9 (кривая 1 ); 0,8 ( 2 ); 0,7 ( 3 ), и от параметра m ( б) при различных значениях ^ _c : п/з (кривая 1 ); 2п/3 ( 2 ); п ( 3 )

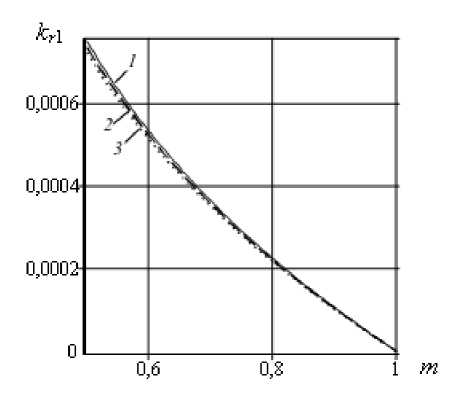
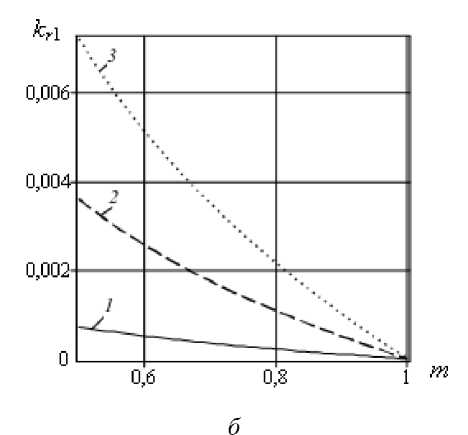
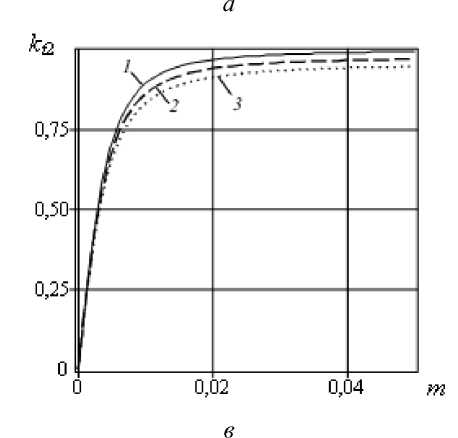
Рис. 4. Зависимости коэффициентов отражения k r 1 ( а , б) и прохождения k t ₂ ( в , г ) от параметра m для координаты надреза ^ c = 0,5 при различных значениях n (фрагменты а , в ): 0 (кривая 1 ); 0,04 ( 2 ); 0,08 ( 3 ); и различных длинах надреза е (фрагменты б , г ) : 0,001 (кривая 1 ); 0,005 ( 2 ); 0,010 ( 3 )

• 3. Обратная задача

Могут быть использованы различные способы определения параметров надреза в стержне в зависимости от измеряемых характеристик волны с помощью приборных средств.

Cпособ 1 . Выделение отраженных и проходящих волн и использование данных измерений перемещения в два момента времени . Выделение отраженных волн может быть достигнуто, например, сравнением данных замеров в точке ^ = 0 стержня с надрезом и в такого же стержня без надреза или сравнением данных в одном и том же стержне по истечении некоторого времени, достаточного для развития наметившегося повреждения. Могут быть и другие способы выделения отраженных волн. Если обозначить через ( u r 1 ) 1 и ( u r 1 ) 2 замеренные значения перемещения в отраженной волне в точке ^ = 0 в моменты времени 1 1 * и 1 * в пределах полупериода колебания, причем для простоты принять 1 * = 0, 1 2 п /2, а через ( u₁ 2 ) 1 — замеренное значение перемещения в проходящей волне в точке ^ 1 = 2 п в момент времени 1 1 * , то из (14) и (18) последует система уравнений:

( u_r 1 ) 1 e ” ^ ^c = ( m ² - 1 ) an ( ( m ² a + 2 mn + a ) sin 22 _c + 2 m ( 2 n a - 1 ) cos 2^ _c ) , ( u_r 1 ) ₂ e ” ^{5 c} = - ( m ² - 1 ) an ( 2 m ( 2 n a + 1 ) sin 2£ _c + ( m ²a + 2 mn + a ) cos 2£ _c ( u t 2 ) i e ” ^{( 2n} - ^ ^c - ^{a )} = 2 m an ( 1 - m ) 2 ( 3 ”a - 1 ) •

Параметры m, t c _c , а определяются из (23) при заданных значениях ( u_r 1 ) 1 , ( u_r 1 ) 2 , ( u t 2 ) 1 и n . Система (23) может быть решена численно. Например, для ( u r 1 ) 1 = 0,0004, ( u_r 1 ) 2 = 0,0007, ( u t 2 ) 1 = - 0,0002 параметры равняются: m = 0,4485; £ _c = 0,4852; а = 0,0009.

Если один из параметров m, ^ _c , а известен, то для нахождения двух остальных могут быть использованы следующие способы.

Cпособ 2 . Выделение отраженных волн, использование данных измерений амплитуды и фазы волны . При обозначениях последних через ( u_r 1 )_1max и ( ф _r 1 ) из (20) следует

( u r 1 L = 4 A r i+ B^ , tg ( ф r 1 ) = - B r J A r 1 . (24)

Cпособ 3 . Измерение перемещений в суммарной волне в два момента времени . Обозначая в (13), (14), (18) через ( u s ) 1 и ( u s ) 2 максимальные значения перемещения в точке £ = 0 в суммарной волне в моменты времени 1 1 * = 0, 1 2 п /2, приходим к системе:

( u s ) 1 e ” ^{5 c} = ( m ² - 1 ) an ( ( m²a + 2 mn + a ) sin 2^ _c + 2 m ( 2 n a - 1 ) cos 2^ _c

[ ( u s ) ₂ - 1 J e ” ^{5 c} = - ( m ² - 1 ) an ( 2 m ( 2 n a + 1 ) sin 2^ _c + ( m ²a + 2 mn + a ) cos 2^ _c

Cпособ 4. Измерение амплитуды C и фазы δ суммарной волны . При этом из (21)

следуют уравнения

C = V С + c 2 ,   tg ( 8 ) = - C /C 2 ,

где C 1 ( m , ^ _c , а ) и C ₂( m , ^ _c , а ) определяются в соответствии с (22).

Cпособ 5. Измерение фаз . Если известны сдвиги фаз в отраженной ϕ r 1 и проходящей ϕ r 2 волнах, то могут быть использованы формулы (20).

Cпособ 6 . Измерение коэффициентов отражения k r 1 и прохождения k t 2 . Из соотношений (20) следует, что по известным коэффициентам отражения k r 1 и прохождения k t 2 можно определить два из трех параметров m , ξ c , ε .

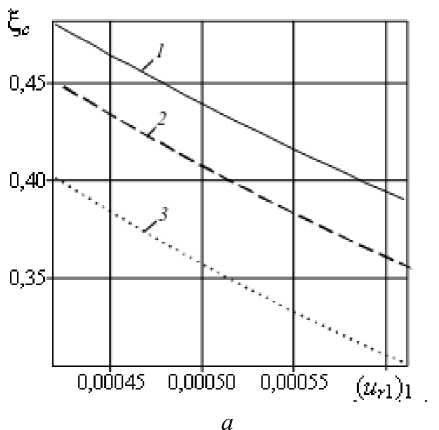
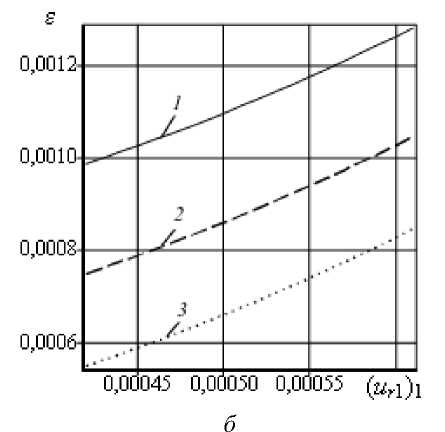
На рисунке 5 приводятся зависимости координаты надреза ξ c , длины надреза ε и параметра m от ( u r 1 ) 1 для различных значений ( u r 1 ) 2 , при ( u t 2 ) 1 = - 0,0002 и коэффициенте затухания n = 0,08 . Кривые показывают, что по трем замеренным значениям ( u r 1 ) 1 , ( u r 1 ) 2 , ( u t 2 ) 1 определяются координата надреза ξ c , длина надреза ε и параметр m.

Возможно использование и других измерений параметров падающей, отраженной от надреза и проходящей волн.

Требование повышенной точности измерений с помощью приборных средств и регуляризация в обратной задаче являются обычными. Они здесь не рассматриваются.

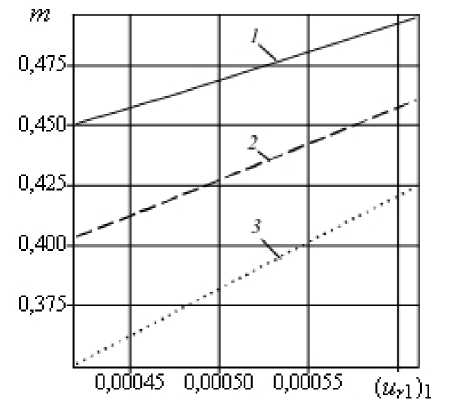
в

Рис. 5. З ависимости координаты надреза ξ c ( а ), длины надреза ε ( б ) и параметра m ( в ) от ( u r 1 ) 1 при ( u t 2 ) 1 = - 0,0002 и коэффициенте затухания n = 0,08 для различных значений ( u r 1 ) 2 : 0,0007 (кривые 1 ); 0,0006 ( 2 ); 0,0005 ( 3 )

Анализ отраженных и суммарных волн в стержне позволяет сделать вывод о том, что амплитуда и сдвиг фазы зависят от величины и положения надреза. При этом зависимость сдвига фазы в отраженной волне от положения надреза ξ c имеет периодический характер. Получено, что длина надреза ε и параметр m практически не влияют на сдвиг фазы. Таким образом, сдвиг фазы в отраженной волне можно использовать для определения координаты надреза или зарождающегося повреждения.

Полученная методика может использоваться при  разработке системы диагностирования повреждений длинных стержневых систем.

Работа выполнена при финансовой поддержке   Российского фонда фундаментальных исследований (проект № 08-01-97008-р_Поволжье_а).