Отражение волн от подвижного упругого слоя в многомодовом волноводе

Волноводные структуры применяются для передачи энергии и информационных сигналов в широком диапазоне длин волн и по волнонаправляющим физическим свойствам обычно имеют взаимные (одинаковые) свойства в прямом и обратном направлениях. Несимметрия структуры и внешние воздействия часто могут стать причиной невзаимности структур для волн, распространяющихся во взаимно противоположных направлениях (это свойство хотя и ограниченно, но уже используется в так называемых невзаимных устройствах СВЧ-, КВЧ- и оптического диапазонов: это ферритовые вентили, циркуляторы, фазовращатели) [4]. Вместе с тем невзаимные свойства волнонаправляющих структур, независимых от их физической природы, не рассматривались.

Рассмотрим эффект Доплера для основной и высших мод многомодового волновода со слоем магнитодиэлектрика, движущимся вдоль оси волновода. Основные свойства могут быть рассмотрены на модели плоского волновода (рис. 1). Пусть однородный слой среды 2 толщиной d с показателем преломления n2 = ^Б2Р2 движется с постоянной скоростью u вдоль оси волновода Ох. Координата левого края слоя описывается во времени зависимостью x = ut, правого - x = ut + d. Слева от границы расположена среда 1, характеризуемая показателем преломления n 1 = ^Б1Ц1. Справа -среда 3 с показателем преломления n3 = ^б3ц3 . Скорость распространения волн в первой среде равна с 1, в третьей - с3. Во второй среде с учетом её движения вдоль оси волновода Ox скорости волн в прямом и обратном направлениях в общем случае различаются с21 * с22. Для анализа особенностей отражения электромагнитных волн, падающих из области 1 на поверхность подвижного слоя, ищется решение волновых уравнений в областях 1–3 с учетом граничных условий на стенках волновода Eт (у = 0, d) = 0 и на подвижных границах раздела сред (x = ut) в виде

E 1 z ^{( x} ) = E 2 z ^{( x} ) ,

H 1 у ⁽ x ) = H 2 у ⁽ x ) ^, E 2 z ⁽ x + d ) = E 3 z ⁽ X + d ) , H 2 у ( ^{x +} d ) = H 3 у ( ^{x +} d ) .

Анализ показывает, что решение существует в том случае, когда частоты падающих и отраженных волн в каждом из слоев в общем случае различны. Решение в каждой из областей ищется в виде [5]:

E 11 z = A 11 ^s i ⁿ k z z ^ex P [ i ( ^ю t — k 11 x ) ] ’ E 12 z = A 12 ^sin k z z^exP [ i ( ® 1 t ^{+ k} 12 ^x ) ] ,

	z .	a
	CDi — G) -	C21	CO -^- 3
	E 1	62 Ц2 2	u 3	X

Рис. 1. Отражение и прохождение волн через подвижный слой в волноводе

Fig. 1. Reflection and transmission of waves through a moving layer in a waveguide

_ ^k11 д   i l « ^uk 11 ) t ,^k 12 д   i ⁽« 1 ^{+ uk} 12 ) t_

A11 e         +    A12 e—

P1

- ^k21 д _p ( ( « 2 ^{— uk} 21 ) t .^k22 _д    i ( « 3 ^{+ uk} 22 ) t

=     A21e         +    A 22e, p2

i «₂ d                      i « 3 d

А p c 21 p i ⁽« ^{— uk} 21 ) t         c 22 p i ⁽« 3 ^{+ uk} 22 ) t _

21 e e           + 22 e e           —

x <  0,

E 21 z

E 22 z

= A 21

= A 22

sin k z z exp i («. 2 t + k 21 x ) ; sin k z z exp i ( « 3 1 — k 22 x ) ,

i « 4 d

• -А p c 31 p i ⁽ «4 ^{— uk} 31 ) t

• — 31 e e            ,

i «₂ d

• _ k 214 P c 21 p i ⁽ «2 ^{+ uk} 21 ) t ,

A 21e     e          + p2

i « 3 d

• ₊ k 22 A e c 22 e i ⁽« 3 ^{+ uk} 22 ) t =

P 2 ²²

i«4 d kSLA p c 31 pi («4 — uk 31) t

A 31 e     e p3

x <  0 <  d ,

E 31 z = A 31 sin k z z exp ^ i ( « 4 1 — k 31 x ) ] ,

x >  d , где в общем случае волновые числа прямых и обратных волн могут различаться k ^ ^ k ^, k 21 ^ k 22 .

Проекция волнового числа на ось Oz с учетом граничных условий в плоскостях у = 0, у = а равна k zm = m ^л / а , m = 1,2,3... — индекс моды. Продольные волновые числа определяются соотношениями:

^k 11 = ^k 12

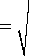
„ 2

2 «     ,2

Пи--К

1 2 zm c

k 21 =

2 « 2, n ² .2

c 21

—

k

. 2

zm

I ю 2    „ v     22 «L_k2 ,

22 2 2 2      zm ^,

V ^c 22

^k 31 =

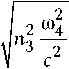
2 2 k_zm

Для кусочно-однородной конфигурации преобразования мод на границах раздела сред не происходит. В этом случае распространяющиеся в волноводе моды, характеризуемые индексами m , между собой не взаимодействуют, и можно независимо рассматривать распространения и отражения отдельно каждой моды. Подстановка искомых решений в граничные условия для компонент поля E z , Н у при x = ut , x = ut + d дает соотношения между амплитудами A ^ и частотами « i для каждого типа волн с произвольным индексом m , который для простоты записи в системе уравнений опускается:

i ( «- uk 11 ) t         i ( « 1 + uk 12 ) ^t _

A 11 e         + A 12 e          —

Pi ( « 2 ^{— uk} 21 ) t + д i (( «3 ^{+ uk} 22 ) t

= A 21 ^{e          +} A 22 ^e          ,

Эти соотношения должны выполняться для любого момента времени t , что приводит к условию « — ukn ( « ) = « 1 + uk 12 ( « 1 ) = « 2 — uk 21 ( « 2 ) = = « 3 ^{+ uk} 22 ( « 3 ) = « 4 ^{— uk} 31 ( « 4 ) .

Отметим, что частоты « 1 - отраженной от левой границы подвижного слоя волны в первой среде, волны, « ₂ - прошедшей во вторую среду, частота волны во втором слое « 3 , отраженной от правой границы подвижного слоя 2, частота « ₄ волны, прошедшей в среду 3, в общем случае отличаются от частоты падающей волны « и зависят:

от скорости движения границы раздела сред u , от скорости движения каждой из сред и , и , U 3 , от типа волноводной структуры и индекса моды m . Следует отметить, что соотношения выполняются

для различных типов кусочно-однородных вдоль оси Oz волноводных структур.

Рассмотрим основные особенности, которые вносит поперечная вариация поля. Частота « 1 отраженной от подвижного слоя волны с индексом m определяется через частоту « падающей на

границу волны с тем же индексом уравнением

« — uk11 mz («) = «1 m + uk12mz («1 m ), которое для плоской структуры, показанной на рис. 1 может быть представлено в виде

«-

« ²

un

\ 1 c c²

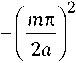
2 « ²

= « + u n

^{1        1} c ²

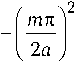
(здесь c 1 = c ). Для волновых чисел падающей и отраженной волн имеем соотношение

2fc2-fc2 ⁿ 1 ^k    k zm

—

2 k zm .

Физика волновых процессов и радиотехнические системы. 2021. Т. 24, № 2. С. 73–78

Physics of Wave Processes and Radio Systems, 2021, vol. 24, no. 2, pp. 73–78

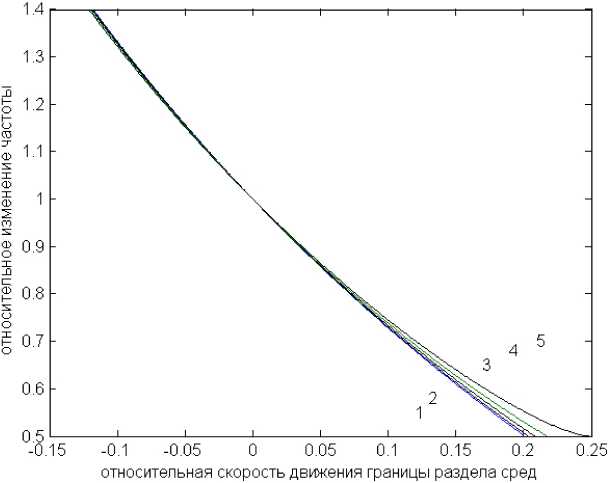
Рис. 2. Зависимость изменения частоты о 1 / го отраженных волн от относительной скорости u / c движения границы раздела сред (1 - m = 0; 2 - m = 1; 3 - m = 2; 4 - m = 3; 5 - m = 4, n c / о a = 0,2, n = 1)

Fig. 2. Dependence of the change in the frequency о 1 / о of reflected waves depending on the relative velocity u / c of the movement of the interface between the media (1 - m = 0; 2 - m = 1; 3 - m = 2; 4 - m = 3; 5 - m = 4, n c / о a = 0,2, n = 1)

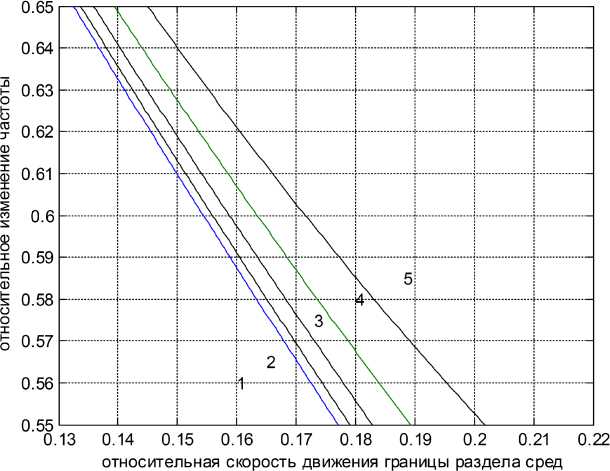
Рис. 3. Зависимость изменения частоты О 1 / о отраженных волн от относительной скорости u / c движения границы раздела сред (1 - m = 0; 2 - m = 1; 3 - m = 2; 4 - m = 3; 5 - m = 4, n c / о a = 0,2, n = 1)

Fig. 3. Dependence of the change in the frequency о 1 / о of the reflected waves depending on the relative velocity u / c of the movement of the interface between the media (1 - m = 0; 2 - m = 1; 3 - m = 2; 4 - m = 3; 5 - m = 4, n c / о a = 0,2, n = 1)

Частота отраженной волны о 1 в волноводе, включающего движущуюся границу раздела сред, зависит от номера моды m .

На рис. 2–3 показана зависимость относительного изменения частоты отраженных волн от относительной скорости движения границы раздела сред u / c для различных мод. Если слой 2 неподвижен, тогда u / c <  0, как и следовало ожидать, эффект Доплера не наблюдается ( о 1 / о = 1).

Увеличение частоты

с - и о4 = —--о с3 - и

наблюдается

при движении слоя навстречу волне ( и / c <  0 ) , уменьшение частоты ( о 1 / о <  1 ) наблюдается при

«убегании» слоя от волны ( и / c >  1). Случай m = 0

соответствует одномерной структуре и сводится к известному соотношению [1; 2]:

с - и о =----о .

с + и

С увеличением индекса моды m скорость изменения частоты № 1 / № в зависимости от скорости движения границы раздела сред и / с уменьшается и при некотором критическом значении скорости ( и / с >  1 ) , различном для разных мод m , зависимость № 1 / № принимает аномальный характер: уменьшение частоты с ростом скорости меняется на увеличение частоты. При этом сохраняется условие ( № 1 / №< 1 ) .

Частота отраженной волны № 1 m зависит от индекса возбуждаемой моды m . Это означает, что если граница раздела 1 и 2 сред является неоднородной (например, слой переменной толщины), то отражение от границы раздела сред в волноводе сопровождается возбуждением высших мод и каждой моде соответствует свой доплеровский сдвиг отраженной волны, и спектр отраженного сигнала обогащается увеличением числа мод и увеличением числа частот в отраженной волне.

Движение слоя приводит к тому, что каждой моде соответствует отдельная частотная составляющая № 1 m эффекта Доплера, формируется многомодовый и соответствующий ему многочастотный эффект Доплера [3].

Для волны, прошедшей в третью область, частоты мод прошедших волн № 4 m в общем случае отличаются от частоты волны, падающей на границу раздела подвижного слоя, и определяются уравнением

^{№ — uk} 11 m ( ^№ ) = ^№ 4 m ^{— uk} 31 m ( ^№ 4 m ) •

В частности, для плоской структуры:

^№ 2

№ — U    П ²

У с ² 1

—

m п

2 a

I = ^№ 4 m

—

№4 m „2 n с2   3

—

m п

2 a

.

Частоты прошедших в третью сред мод не

за-

висят от параметров второй среды. Отметим, что если параметры первой и третьей сред одинаковые ( n i = n з ) , то прохождение моды m = 1 не приводит к сдвигу частоты прошедшей волны и № = № 41 . Однако частоты прошедших волн более высокого порядка ( m >  1 ) , которые могут возбуждаться неоднородностями структуры, не совпадают с частотой падающей волны ( №*№ 41 ) . В частном случае m = 0 подвижной границы раздела в свободном пространстве ( и / с * 0 ) имеем известные соотношения для отраженной и прошедшей волн:

С — и

№ 1 =----- № ,

С 1 + и

С — и № 4 =----- № .

^С 3 ^{— и}

Для прошедшей волны уменьшение или увеличение частоты доплеровского сдвига зависит от соотношения скоростей распространения волн в первой и третьей средах, и, если скорости волн в этих средах совпадают, доплеровский сдвиг для прошедших волн не наблюдается [6; 7].

В многомодовых волноводных структурах с подвижными средами может наблюдаться эффект Доплера для каждой моды, доплеровский сдвиг частоты зависит от индекса моды, в случае неоднородной структуры будет наблюдаться многомодовый эффект Доплера: отражение многих мод с различными частотными сдвигами по отношению к частоте падающей на неоднородность волны.

Заключение

Изучено влияние невзаимности параметров сред, заполняющих волноводную структуру, на параметры акустических и электромагнитных волноводов. Невзаимность структуры приводит к изменению критических длин волн или частот мод, распространяющихся в волноводе, в частности, к изменению количества распространяющихся мод. Движение среды, вызывающее невзаимность параметров, приводит к изменению волновых чисел и наиболее существенно при скоростях движения сред, сопоставимых со скоростью распространения волн в неподвижной среде.

Рассмотрено прохождение волн через подвижную границу раздела сред в волноводе. Получены соотношения для расчета частот отраженных и прошедших подвижную границу раздела сред в волноводе для основной и высших типов волн в зависимости от скорости движения границы раздела сред и самих сред. При наличии неоднородностей, вызывающих порождение многомодового режима, возникает формирование многокомпонентного спектра частот, соответствующих модовым компонентам, многочастотного эффекта Доплера для отраженных и для прошедших неоднородность волн.

Установлено, что отражение от движущейся границы раздела сред приводит к зависимости изменения частоты отраженного сигнала как от скорости движения границы раздела сред, так и от номера моды. Для высших типов волн эта зависимость наименьшая для малых скоростей движения границы иус <  0,3 и наибольшая при больших скоростях и/с >  0,7.

Физика волновых процессов и радиотехнические системы. 2021. Т. 24, № 2. С. 73–78

Physics of Wave Processes and Radio Systems, 2021, vol. 24, no. 2, pp. 73–78