Отрицание мультиплексора

В работах [1–3] предложены избыточные, так называемые функционально полные толерантные (ФПТ), базисы для реализации логических преобразователей отказоустойчивых, адаптируемых к отказам автоматов. Остаточные базисы соответствующих логических элементов позволяют с помощью реконфигурации схемы логического преобразователя, например, так, как это возможно в программируемой логической интегральной схеме (ПЛИС), реализовать хотя бы часть наиболее важных функций. Такой подход соответствует внутренней избыточности по терминологии теории надежности в отличие от внешней – структурного резервирования [3].

Особенность представления бинарных переключательных функций в избыточных

(функционально полных толерантных) бази- сах):

X 1 X 2 V x 3 x 4 ,

(x 1 V X2)(x3 V X4)(2)

заключается в двойственности базиса и необ- ходимости представления произвольной функции в виде f = f1.1. f 1.2 V f 21 f 2.2, _ f = (f 1.1 V f 1.2)(f 2.1 V f 2.2).

Поэтому при синтезе схем автоматов в избыточных функционально полных толерантных (ФПТ) базисах возникает необходимость отрицания (инверсирования) ортогональных по некоторым переменным конъюнкций дизъюнктивной нормальной формы – ДНФ и конъюнкций в конъюнктивной нормальной форме – КНФ.

1. Правило отрицания ортогональных конъюнкций ДНФ бинарных переключательных функций

a

b

c

dx

—

—

-   0

-

-

Пусть задана бинарная переключательная функция:

-

-

ax i v bx_x .

Получим ее отрицание (инверсию), ис- пользуя закон Де-Моргана:

В матрице (11) каждая строка для данного значения развязывающей переменной преобразуется в количество строк, равное числу переменных перед x .

ax i v bx_r =

= ( a v x_r )(b v x i ) =

• 3.    Отрицание ортогональной дизъюнкции КНФ

= ab v ax i v xb v x_rx 1 .

Покажем, что

Исключая первую конъюнкцию по закону обобщенного склеивания, а последнюю по закону противоречия, получим:

ax i v bx_x = ax 1 v bx_x .

Представим это правило в матричной форме:

( a v x 1 )( b v x j ) =

= ( a v x 1 )( b v x^ ).

Использ уем дистрибути вный закон:

( a v x 1 )( b v x_l ) =

abx		abx
1 - 0	^	0 - 0
- 11		- 01

= ax_Y v bx 1 =

( a v bx, )( x_l v bx 1 ).

Поэтому, учитывая закон Порецкого

Здесь отрицается (инверсируется) диагональ "a-в". Это правило инверсии ДНФ с так называемой развязывающей (ортогональной) переменной x .

( a v bx, )( x j v bx 1 ) =

= ( a v b )( a v x 1 )( b v x_t ).

Далее, применив закон обобщенного

склеивания, получим:

( a v x 1 )( b v x_l ).

2. Инверсирование двух сложных ортогональных конъюнкций

Рассмотрим пример инверсии 2 ортогональных конъюнкций из трех переменных каждая:

abx v cdx = ( a v b v x )( c v d v x ) =

= / / v /d v ax v b / v b d v bx v xc v v xd v xx =            (9)

= ax v bx v xc v xd =

= ( a v b ) x v ( c v d) x .

• 4.    Отрицание ортогональных ДНФ

Усложним конъюнкции перед x , т.е. введем ортогональные ДНФ:

( ab v c ) x v ( de v f ) x .        (16)

Применяя вышеприведенное правило, получим:

( ab v c ) x v ( de v f ) x =

( a v b ) cx v ( d v e ) fa ..

Иначе:

acx v bcx v dfx v efa .

В табличной форме:

Таким образом, инверсия матрицы: abcdx

11 - - 0

- - 111

приводит к матрице:

Исходная таблица 1

a	b	c	d	e	f	x
1	1	-	-	-	-	0
-	-	1	-	-	-	0
-	-	-	0	0	-	1
-	-	-	-	-	0	1

Инверсная таблице 1 таблица 2

a	b	c	d	e	f	x
0	-	0	-	-	-	0
-	0	0	-	-	-	0
-	-	-	1	-	1	1
-	-	-	-	1	1	1

• 5.    Использования правила отрици-ния в самосинхронных автоматах

Самосинхронный автомат строится путём введения двойственного (бифазного) канала и индицирования входных и выходных сигналов [4, 5] (рис. 1):

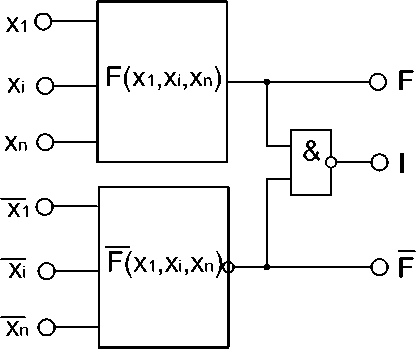
Рис. 1. Самосинхронный комбинационный автомат с индикацией только выходных сигналов

Так, предлагается ФПТСС элемент – функционально полный толерантный элемент (элемент с избыточным базисом) самосин-хронный (рис. 2):

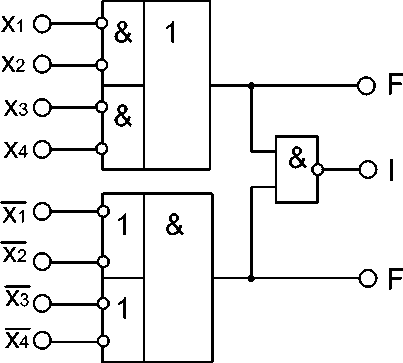
Рис. 2. Базовый ФПТСС элемент

Один канал реализован на избыточном базисе:

x 1 x 2 v x 3 x 4 (2ИЛИ-2И-НЕ), двойственный канал реализован на избыточном базисе (2И-2ИЛИ-НЕ):

( x 1 v x 2 )( x 3 v x 4 ).

Парафазные переменные подаются через дополнительное устройство – формирователь спейсера[4, 5], не указанные на рис.2.

В случае обнаружения отказов (кроме отказов выходов), например, при фиксации незавершения переходного процесса, возможно использование остаточного базиса, общего для двух элементов.

Однако в ряде случаев двойственный канал может быть построен иначе. Так, для реализации исключающего ИЛИ (суммы по модулю два), например, некоторых переменных A, B:

Ab v ab .(19)

Используя базис

(x 1 v x2 )(x3 v x4 ) = xx v x3x4,(20)

можно пол учить

AB v AB = AB v AB, соответственно, двойственная функция будет

Ab v aB = ab v AB..(22)

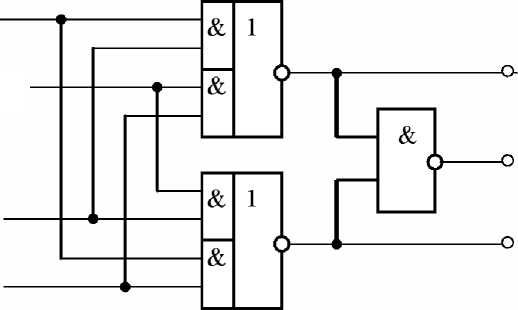
Таким образом, в выражениях (21), (22) используется также правило инверсии. Само-синхронная реализация [4–5] представлена на рис. 3.

На рис. 3 АВ – бифазное А (не А), ВВ – бифазное В (не В), Y – выходной сигнал, YB – бифазный выход (не Y), I – выход индикатора окончания переходного процесса. Основной канал реализует функцию

AB v AB = AB v AB ,       (21)

двойственный –

AB v AB = AB v AB. (22)

То есть двойственность реализуется за счёт только входных сигналов в отличие от схем рис. 1, 2.

A(0)AB (0)

B(0)BB(0)

Y(l)

1(0)

YB(1)

Рис. 3. Самасинхронная реализация функции исключающего ИЛИ (суммы по модулю 2)

• 6.    Инверсия выражений

с ортогональностью по нескольким переменным.

Отрицание мультиплексора

Пусть задана функция мультиплексирования с четырех направлений 4–1:

z = ax 2 x 1 V bx 2 x . V

¹             (23)

v cx₂x i v dx₂x_{ .

Преобразуем ее:

z = x 2 ( ax i V bx, ) V

¹               (24)

v x ₂ ( cx i v dx_Y ).

Очевидно, что отрицанием этой функции будет выражение, в котором согласно правилу (3) отрицаются ДНФ в скобках, а они, соответственно, также отрицаются:

z = x 2 ( ax i v bx, ) v

¹                (25)

v x ₂ ( cx i v dx_{ ).

Получаем выражение:

z = ax 2 x 1 V bx 2 x . V

¹               (26)

v cx₂x i v dx₂x_Y .

То есть "отрицание мультиплексора" – это мультиплексор, у которого отрицаются входы данных a,b,c,d.

Поэтому в схеме самосинхронного мультиплексора 2-1AiBi, i=1…8 [5] (рис.4):

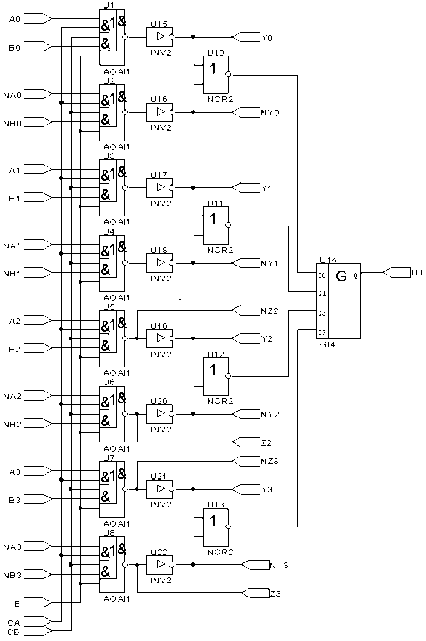
Рис. 4. Самосинхронная реализация мультиплексора 2–1

Оба канала AiBi-NAiNBi (N – бифазные сигналы) реализованы на однотипных элементах АОАI1. То есть первый канал реализует функцию:

Y i = AX V B i X ; X = CA; X = CB .

Двойственный канал реализует отрицание мультиплексора:

NY = NA X ∨ NB X .     (28)

• 7.    Самосинхронный логический элемент конфигурируемого логического блока (КЛБ) программируемой логической интегральной схемы

Современные программируемые логические схемы (ПЛИС) типа FPGA ( field-programmable gate array ) содержат конфигурируемые логические блоки (КЛБ) [6], состоящие из логических элементов ЛЭ, программируемых локальных и глобальных матриц соединений-ЛМС, ГМС (рис. 5)

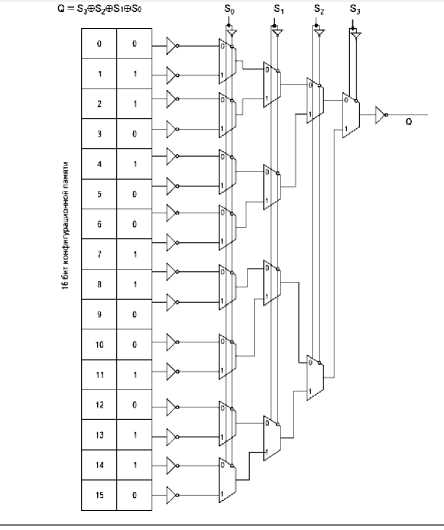
Рис. 6. Логический элемент ПЛИС FPGA

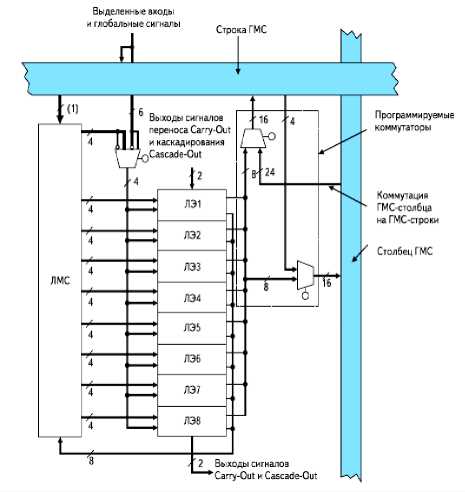
Рис. 5. Конфигурируемый логический блок (КЛБ) ПЛИС FPGA

Причем каждый логический элемент ЛЭ строится как постоянное запоминающее устройство ПЗУ (LUT – Look Up Table), представляющее собой мультиплексор 16–1, входы данных которого настраиваются так называемыми конфигурируемыми ячейками памяти [6] (рис. 6):

На рис. 6 входные сигналы – S0,S1,S2,S3, элемент настроен на реализацию суммы по модулю два S0 ⊕ S1 ⊕ S2 ⊕ S3. Элементарные мультиплексоры 2–1 реализуются так же, как в коммутаторе (это тоже мультиплексор) [6] (рис. 7).

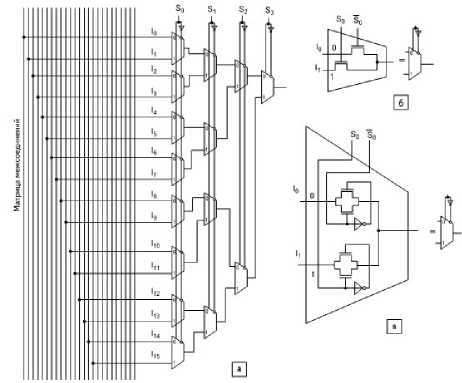
Рис. 7. Коммутатор сигналов с локальных межсоединений на вход КЛБ

Таким образом, для получения второго канала СС схемы - дерева мультиплексоров необходимо проинвертировать данные конфигурируемой памяти (рис. 8):

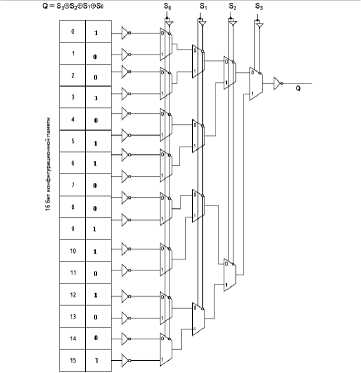
Рис. 8. Двойственный канал самосин-хронного логического элемента ПЛИС FPGA

Таким образом, на базе существующих конфигурируемых логических блоков – КЛБ (рис. 5), содержащих 8 ЛЭ, можно путем доработки (введения индикаторный элементов и блока спейсера) построить 4 самосинхронных элемента.

Заключение

Таким образом, правила отрицания (инверсии) ортогональных конъюнкций ДНФ (дизъюнкций КНФ) позволяют упростить алгоритмы представления произвольных логических функций в избыточных (ФПТ) базисах. Отрицание логической функции мультиплексора – генератора функций n переменных получается путем отрицания переменных данных.

Это позволяет строить самосинхронные логические элементы ПЛИС FPGA путем введения двойственного канала с отрицанием разрядов конфигурационной памяти. Подобное дублирование может быть также использовано для контроля правильности функционирования КЛБ в отказоустойчивых системах.