Overlapped Segmental Active Constellation Extension for the PAPR Reduction of the OFDM-OQAM System

Published Online April 2016 in MECS

Orthogonal frequency division multiplexing (OFDM) is one of the most popular multicarrier modulation schemes which has been widely used in many broadband communication systems [1]. However, each subcarrier of OFDM system uses rectangular pulse shaping, which cause relatively serious out-of-band (OOB) radiations. Besides, the insertion of the cyclic prefix (CP) will reduce the data transmission rate of the OFDM system. In order to overcome the drawbacks of the OFDM systems, the OFDM with Offset Quadrature Amplitude Modulation (OFDM-OQAM) technique has drawn significant interests in recent years [2-3]. OFDM-OQAM systems provide lower side lobes when compared with OFDM system due to the use of pulse shaping filters [4]. Moreover, the OFDM-OQAM systems provide higher spectral efficiency and lower narrow-band interference since it operates without CP [5]. Based on the above advantages, the OFDM-OQAM method has attained as a viable alternative for Cognitive Radio (CR) applications.

However, as a multicarrier modulation technology, the OFDM-OQAM system inevitably produces high peak-to-average power ratio (PAPR), which degrades the efficiency of the high power amplifier (HPA) [6]. In the OFDM systems, much research has been done to deal with the PAPR problem, which can be classified into three categories: signal distortion algorithm, probability algorithm and block coding algorithm. The signal distortion algorithm limits the OFDM signal below a given threshold by nonlinear distortion and includes: signal clipping [7] and companding transformation [8]. The probability algorithm improves the PAPR performance by significantly reducing the probability that large peak power signal appears and optimizing multicarrier signal PAPR statistical properties. It includes selective mapping (SLM)[9], partial transmit sequence (PTS)[10, 11], and tone reservation (TR)[12]. The coding algorithm [13] limits the signals that can be used for transmission, only the signals whose peak value is lower than the maximum peak threshold are allowed to be sent. Among these technologies, Active Constellation Extension (ACE) technique is one of most effective methods. Though ACE technique increases little transmission power, it can effectively reduce PAPR without introducing interference and sending additional side information. The essence of ACE algorithm is to solve the nonlinear programming problem. The computation is usually very large and is not for the project implementation. In practical applications, some approximation algorithms are usually used to solve this problem, such as Projection Onto Convex Sets (POCS)[14,15], Smart Gradient-Project (SGP)[16], and so on. The POCS algorithm can approximate the optimal results in theory, but this algorithm involves Inverse Fast Fourier Transform (IFFT) and Fast Fourier Transform (FFT).

Due to the likeliness between the OFDM and the OFDM-OQAM system, most research in recent years has been focused on employing the conventional PAPR reduction schemes for the OFDM systems in the OFDM-OQAM systems. Whereas, because of the filtered OQAM-OFDM signals are overlapped with adjacent data blocks, it’s not very advantageous to employ these algorithms into OQAM-OFDM systems directly.

In recent years, several schemes for PAPR reduction specifically in the OQAM-OFDM systems have been proposed. The clipping-based technique is discussed for OFDM-OQAM in [17], simulation results show that the algorithm designed for the OFDM system can be fully applied to the OFDM-OQAM system with similar performance in the synchronized case. An overlapped selective mapping (OSLM) scheme was proposed in [18], for this modified algorithm, the current data block and its adjacent data blocks are jointly considered to choose the optimal phase rotation sequence. Besides, a sliding window tone reservation (SW-TR) technique was proposed in [19], which uses the peak reduction tones of several consecutive data blocks to cancel the peak power of the OFDM-OQAM signal inside a window. In [20], an effective partial transmit sequence (PTS) technique is proposed by employing joint multi block Optimization for OFDM-OQAM signals. In [21], a novel segmental PTS (S-PTS) scheme is proposed, the key idea of the S-PTS scheme is to divide the overlapped OQAM-OFDM signals into a number of segments, and then some disjoint sub blocks are divided and multiplied with different phase rotation factors in each segment. Aim at the overlapped structure of the OFDM-OQAM signals, all of the above schemes provide effective solution for the high PAPR problem, and the main idea can be summarized as: deal with the multiple adjacent data blocks simultaneously instead of optimizing each data block independently.

In this paper, we proposed a modified technique called overlapped segmental Active Constellation Extension (OS-ACE) for the OFDM-OQAM system. In this new OS-ACE scheme, the input filtered signals are divided into several segments and then the ACE scheme is operated on each segment. For a better PAPR reduction performance, the adjacent segments are overlapped with each other. The simulation results show that, compared to the conventional ACE scheme directly used in the OFDM-OQAM system, the modified scheme can provides a better PAPR reduction performance while maintain the same BER performance. Furthermore, the OS-ACE scheme used in the OFDM-OQAM system even shows better performance than the conventional ACE scheme for OFDM system.

The rest of the paper is organized as follows. In Section II, OFDM-OQAM system model is illustrated, followed by the modified PAPR reduction schemes being proposed in Section III. In Section IV, simulation results are given to compare the PAPR reduction performances of the proposed technique and the conventional technique. Finally, the concluding remarks are given by Section V.

• II.    Signal Model

In a baseband OFDM-OQAM system with N subcarriers, real valued symbols modulated by offset QAM are transmitted on each sub-carrier, and then the transmitted signal can be written as [2]:

M - 1 N - 1

4 n ] = Ц x^kmg^km [ n ]               (1)

m = 0 k = 0

Where M represents the number of input data block x^k denotes the baseband modulated signal on the k^th subcarrier of the m^th data block, g^k [ n ] represents the pulse shape of index ( m , k ) in the synthesis basis which is derived by the time frequency translated version of the prototype filter function h [ n ] in the following way:

g k [ n ] = h ( n - mN ) e j             (2)

Where фф = n (m + k) - nmk and N represents the number of Subcarriers.

The OFDM-OQAM system model is show in Fig.1, to understand the OFDM-OQAM signal structure better, we rewrite the complex input symbols x^k as:

x m = a^k m + jb^k m ,0 ^ k ^ N - 1,  0 ^ m ^ M - 1     (3)

Where b^k and a^k are the imaginary and real parts of the k^th subcarrier on the m^th symbol respectively. For two successive subcarriers, the time offset T /2 is introduced onto the real part for the first one and onto the imaginary part for the second one where T is the symbol duration, so the number of the input data block M has to be even. Then, the time domain staggered symbols are passed through a bank of transmission filters and are modulated with N subcarriers modulators. Thus, the OFDM/OQAM modulated signal s [ n ] in (1) can be written as

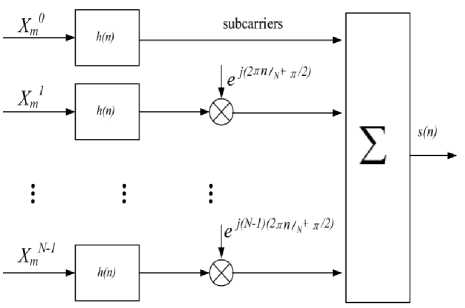
Fig.1. The OFDM-OQAM System Model

M - 1 N - 1                                        N . к

^{s [} n ] = ED a k h ( n — mN ) + jb k h ( n — mN --)] e j m   (4)

m = 0 k = 0                    m             2

Here h [ n ] is the discrete time filter obtained by sampling the continuous time filter h ( t ) , and the length of the prototype filter h [ n ] is LN . Apparently, the OFDM/OQAM filter impulse response has L times the symbol duration, and the time staggered real and imaginary parts of the input symbols, which leads to the overlapping of adjacent data blocks with each other.

The definition of PAPR in the OFDM system is the ratio of the maximum to the average power of the transmitted symbols. Let s [ n ] represents the transmitting complex symbols of duration N , and then the PAPR of this continuous-time baseband signal can be expressed as:

composed of multiple overlapped data blocks, instead of on each data block independently. For our OS-ACE scheme, we firstly divide the overlapped data blocks into several segments and then reduce the PAPR of each segment.

The structure diagram of the modified scheme is showed in Fig. 2. The time domain OFDM-OQAM signal on the m^th data block s [ n ] can be expressed as a superposition of N subcarriers

N - 1              N - 1                  2 n k^_t

PAPR =

max s [ n ] ²

0 <  n <  N - 1

E [| s [ n ]| 2 ]

Where E [] represents the expectation operation. Since the OQAM-OFDM signals are overlapped with adjacent data blocks due to the bank of filters and the time offset between the real and imaginary parts, the conventional definition of PAPR for OFDM systems no longer match perfectly to the OQAM-OFDM systems. However, it was declared that as both systems transmit the equivalent of one complex symbol at the same rate N , we can keep the same measurement for the OFDM/OQAM to provide a fair comparison with the OFDM system.

The PAPR is a random variable, so it is possible to characterize the PAPR distribution (probability that PAPR exceeds a given threshold у ) using complementary cumulative distribution function (CCDF) defined as:

Pr( PAPR > / ) = 1 - ( 1 - e"^y ) N (6)

s m [ n ] = X a m ^ m [ n ] = z x k h ( n ^- mN ) e N e ^    ⁽⁷⁾

k = 0                k = 0

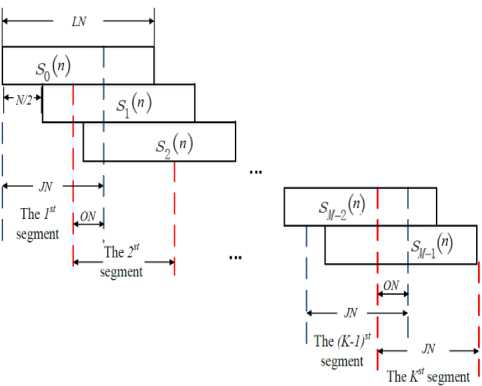
Fig.2. The overlapped segmental scheme for the OFDM-OQAM signals

As the length of the filtered data block is LN (which is the same with the length of the prototype filter) and the overlapped part between two adjacent data blocks is N/2 , we can obtain the overall length of the M input data block:

N z

N oi = - ( M - 1) + LN

• III.    Proposed Active Constellation Exension Scheme

In the OFDM systems, the signal is processed by the conventional clipping scheme in each data block independently. However, the signals in the OFDM-OQAM system are overlapped with multiple adjacent data blocks, and the actual PAPR in a certain time interval depends on several consecutive data blocks [19]. If we conduct the conventional ACE scheme in the OQAM-OFDM systems directly, the peak signal in each data block may be decreased. However, the True PAPR in a certain time interval might not be reduced effectively, since the current data block is affected by multiple consecutive data blocks. Therefore, directly applying the conventional ACE technique to the OFDM-OQAM systems is not very effective.

In the OFDM-OQAM system, since the adjacent filtered signals are overlapped with each other, we conduct the ACE scheme on the signal which is

As can be seen from Fig.2, the overlapped signal is divided into P segments and the length of each segment is JN , where J is an integer no less than 1 . The overlapped part of two adjacent segments is expressed as ON . The value of O ranges from 0 to J-1 . Notice that O cannot be equal to J , otherwise the OS-ACE scheme wouldn't make sense. Theoretically, the larger the length of each segment J , the more data blocks can be processed each time, so the better the PAPR performance. However,when J is larger than L , the performance improvement will not be significantly any more. That is because the length of each filtered data block is LN , and only the overlapped part of adjacent data blocks can have influence on the former data blocks. The PAPR performances with different J and O are given in Section IV.

Specifically, when J=1, O=0, it means each segment is the same length as one data block and there is no overlap between two segments. Under this special circumstance, the modified OS-ACE scheme is just equal to the conventional ACE scheme.

After J and O are defined, the number of the segments P can be obtained by:

N ol    - ( ^M — 1)/ ² + ^L

JN - ON     J - O

Where po~| means the round up operation. As M represents the number of input symbols and is usually set larger than four figures, L is usually set as 4. Considering M >>  L , L can be ignored and the simplified expression of P can be obtained by:

P -

M

2( J - O )

From equation (10) we can conclude that the number of the segment is primarily determined by J-O, which represents the time offset between two adjacent data blocks.

Then the filtered signals are divided into P segments and the modified OS-ACE scheme is conducted on each segment. Assume that the previous p - 1(1 <  p <  P ) segments have already been processed, then extract the signal s [ n ] in the p^th segment from s [ n ] , and s [ n ] can be expressed as:

sm[n],(P —1)(JN — ON) < n < (P —1)(JN — ON) + JN sp [n' i --;o,

else

Step1: Operating the clipping scheme on the signal s [ n ] in the p^th segment. If the amplitude of s [ n ] exceeds the preset threshold, it will be clipped to A, otherwise s [ n ] will remain unchanged. Then the clipped signal can be written as:

Sp ^{[ n 1 -}

s p [ ⁿ L

" A^, [ n ¹

I Sp [n 1 < A ,1 Sp[ n1 > A

Where ф [ n ] is the phase of s_p [ n ]. It can be seen from (12), the phase information of s [ n ] remain unchanged after clipping operation.

Step2: The negative clipped portion of the signal c[n]is calculated as c„ [ n 1 -*

^p       0

f А_езФ_Р ^{[ n 1}

^- s p ^{[ n 1}

s p ^{[ n 1} >  A s p ^{[ n 1} <  A

Step3: Demodulate c[n]to obtain the extension regions Cm[k] where m and k represents the pth segment frequency domain symbol and subcarrier respectively.

Step4:  maintain only those real and imaginary components of Cm [k] which fall within the allowable extension regions and set the rest to zero.

Step5: For oversampling or digital frequency domain filtering, set OOB components to zero, i.e., null all points greater than N.

Step6: Modulate C^m [ k ] to obtain the time domain portion of the corrected clipped signal c ˆ [ n ] .

Step7: And add c ˆ [ n ] to the original time domain signal s_p [ n ] to obtain s_p [ n 1

ssp[ n 1 - sp[ n1 + c:p[ n1                    (14)

Step8: transmit s ˆ [ n ] if it meets PAPR requirements, otherwise repeat from step (1) replacing s [ n ] with s ˆ [ n ] .

After the signal in the p^th segment has been Active Constellation extended, increase p by 1 and repeat the procedure until all P segments have been processed.

Since the proposed OS-ACE scheme reduces the PAPR by correcting the distorted constellations of P consecutive overlapped data segments. As for the proposed OS-ACE scheme, the data in the overlapped part need to be compared twice, which will result in ON more complex additions ( O is the Overlapped factor and usually set less than J ), so the increase of complexity in the modified scheme can be ignored in the OFDM-OQAM system, by considering a reasonable value for O so the computational complexity and the PAPR reduction performance can be well balanced.

• IV.    Simulation Results

  In this section, the PAPR reduction performance and the BER performance of the proposed OS-ACE technique are conducted for comparison. The OFDM-OQAM system employs 64 subcarriers with 5000 input data blocks. The length of the prototype filter h[n] is set as 4 N , which means the time duration of the filtered signals is about four times of that of the input signals. The Complementary cumulative distribution function (CCDF) is applied  as  measurement of PAPR reduction

performance in the simulations.

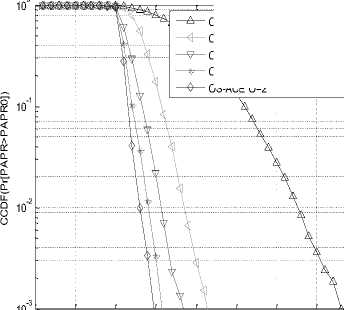
Firstly, we compare the PAPR performance of the modified OS-ACE scheme with different lengths of the overlapped part O . In the simulation, the clipping ratio is CR=1.8 , the length of each segment is set as 3N, i.e. , J= 3 ; and the length of the overlapped parts is O=0, 1, 2, where O=0 means there is no overlap between adjacent segments. It can be seen from Fig.3 that the OS-ACE scheme is effective in reducing the PAPR for the OFDM-OQAM system, and a larger O can improves the performance of the OS-ACE scheme a little.

The PAPR performance of the OS-ACE scheme with different J is shown in Fig. 4. It Is obvious that the overlapped segment structure is quite effective in reducing the PAPR and among all simulated conditions, the best PAPR reduction performance is achieved with J=5, O=4. It can also be concluded from the results that the larger the length of each segment J, the better the PAPR reduction performance. When J is increased to 4, the performance difference can be ignored. Besides, the increasing of O can also help to improve the PAPR performance, but the performance improvement is not as evident as that of when J increases. From equation (9) we can know that the number of the segments P is determined by (J-O), and a larger O means higher computational complexity. As a result, we will use J=4, O=2 in the following simulations to reduce the calculation costs.

Fig.5 shows the proposed PAPR performance of OS-ACE technique with different thresholds conditions. The clipping ratios are: CR1=1.8, CR2=1.9, CR3=2.0 . For the OS-ACE scheme, the length of each segment is J=4 , and the overlapping length is set as O=2 . It can be concluded that the best PAPR performance in the CCDF range from 10 ^{- 2} to 10 ^{- 3} is achieved with CR=1.9(5.58dB) . Therefore, we fixed CR=5.58dB in the following simulations for the OS-ACE technique.

In addition, the PAPR reduction performance of the OFDM system and the OFDM-OQAM system are compared in simulation. Both of the systems employ 64 subcarriers and 5000 input data blocks. The clipping ratio is set as CR=1.9 in the conventional and the modified ACE schemes. From the simulation results shown in Fig.6, we know that the conventional ACE scheme directly used in the OFDM-OQAM system is not as effective as that used in the OFDM system. However, when the modified OS-ACE scheme is applied, the PAPR reduction performance of the OFDM-OQAM system is better than that of the OFDM system with the conventional ACE scheme.

OFDM-OQAM Original

OFDM-OQAM Conventional ACE

OS-ACE O=0

OS-ACE O=1

OS-ACE O=2

PAPR0(dB)

Fig.3. PAPR performance of the OS-ACE scheme with different O (overlapping values)

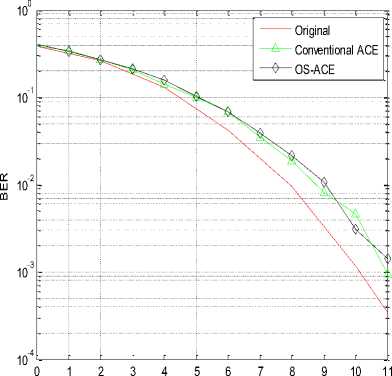
The Bit Error Rate (BER) performance as a function of Signal to Noise Ratio (SNR) is shown in Fig. 7. As in the simulations above, the clipping ratio of both ACE scheme is CR=1.9 , and J=4, O=2 is set for the modified OS-ACE scheme. As can be seen from the results, the BER performance of the conventional ACE scheme decreases the SNR by about 1dB at BER=10^-3, and the modified OS-ACE scheme shows almost the same performance as the traditional ACE scheme. Considering the better PAPR reduction performance, we can conclude that the proposed OS-ACE scheme can improve the performance of the whole OFDM-OQAM system.

10-1

10-2

10-3

rWWWSM

OS-ACE J=2,O=1

OS-ACE J=4,O=1

OS-ACE J=4,O=2

OS-ACE J=4,O=3

OFDM-OQAM Original

OFDM-OQAM Conventional ACE

3        4        5        6        7        8        9       10       11

PAPR0(dB)

Fig.4. PAPR performance of the OS-ACE scheme with different J and O

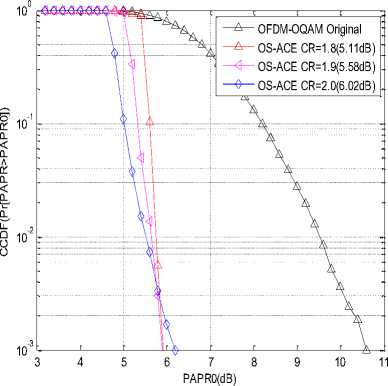
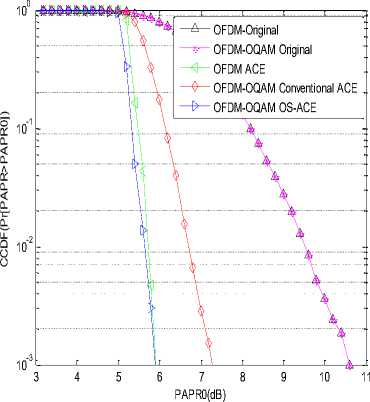
Fig.6. PAPR performance of the OFDM and the OFDM-OQAM system

SNR dB

Fig.7. BER performance of the OS-ACE scheme

• V.    Conclusion

In this paper, a Modified OS-ACE scheme is proposed to reduce the PAPR of the OFDM-OQAM system. Considering the overlapped structure of the OFDM-OQAM signals, the modified OS-ACE scheme divides the filtered signal into a number of segments and each segment is composed of multiple consecutive data blocks. Therefore, the influence of adjacent overlapped data block can be eliminated and the PAPR during a certain time interval can be reduced effectively. In addition, the overlapped structure of the adjacent segments can further improve the PAPR reduction performance. The simulation results showed that the proposed OS-ACE technique provides a better PAPR reduction performance than the OFDM-OQAM system with conventional ACE scheme. Still, the BER performance remained unchanged. Besides, the OFDM-OQAM system with the OS-ACE scheme even outperformed the OFDM system with the conventional ACE scheme.

Acknowledgements

The author is very much thankful to the potential reviewers for their critical comments and suggestions to improve the quality of the manuscript.