P-адическое моделирование динамики индекса РТС в зависимости от таймфреймов

Финансовые рынки как система сложны и неустойчивы, происходящие на них ценовые изменения финансовых активов представляют собой стохастический процесс, что связано с огромным числом сделок между участниками рынка по купле/продаже активов. Кроме ценовых изменений, стохастическими процессами являются броуновское движение и случайные блуждания в физике.

Достижения в физике по изучению неупорядоченных стохастических систем велики, поэтому знания из физики стали применять к исследованию стохастических процессов в экономике. Первые попытки моделирования и анализа финансовых (экономических) систем с использованием физических аналогий относят-

ся к 1936 г. и были сделаны Э. Майораном, итальянским физиком-теоретиком. Но в то время сходства между финансовыми и физическими системами изучались эпизодически, а сама мысль о таком сходстве была неортодоксальной. Позднее, с 1990-х гг., активность исследований экономики с использованием методов физики увеличилась: стали организовываться конференции, издаваться новые междисциплинарные журналы.

Привнесенное изменение из физики в экономику заключается в том, что главным элементом в моделировании процессов является эмпирический анализ экономических данных [12]. Также новшества заключаются в теории и методах моделирования стохастических систем. Наука, которая использует физические методы для изучения экономических (неупорядоченных) систем, называется эконофизикой (данный неологизм был введен профессорами физики Р.Н. Мантенья и Г.Ю. Стенли) [13, с. 12]. Методами исследования экономических систем в эконофизике [11] выступают мультифракталь-ный анализ (показатели Хёрста, R/S-анализ), нелинейная динамика (показатели Ляпунова, аттракторы), статистическая физика (уравнение Фоккера - Планка, уравнение Колмогорова, Леви-распределение [22]), искусственные нейросети (кластеризация), р -адический анализ [17-21].

В настоящей статье в качестве метода моделирования финансовых процессов выбирается р -адический анализ, который наиболее детально разработан и изучен в В.М. Жарковым, старшим научным сотрудником НИЛ ОПП Естественнонаучного института при ПГНИУ. Поэтому целью исследования является применение методики р -адического моделирования и прогнозирования для колебаний цен, индексов фондовых бирж, курсов активов, котировок валют на финансовых рынках. Предметом исследования выступает динамика индекса РТС.

Таким образом, проблема анализа финансовых процессов как неупорядоченных и стохастических явлений представляется актуальной не только для участников финансового рынка, но и для ученых в сфере экономики и физики. Решение данной проблемы заключается в изучении р -адической математики, в определении методики р -адического моделирования и прогнозирования, в построении на основе исследуемого функционала элементарных фигур и наиболее типичных случаев финансового рынка.

Основы р-адической математики

Р -адические числа, впервые введенные К. Гензелем в 1897 г., использовались в решении диофантовых (полиномиальных) уравнений

[19, с. 8]. С 1980-х гг. р-адические числа начали применяться В.С. Владимировым и группой И.В. Воловича в математике и физике: были созданы р-адические модели квантовой меха- ники и теории струн, описывающие изменение геометрии пространства на планковских масштабах [2; 3]. В последнее время в ряде работ было показано, что р-адические числа хорошо приспособлены для описания фракталов [1; 4], в 2000-х гг. В.М. Жарковым разработана методика [5-9; 23] по изучению экономических про цессов с помощью р-адического анализа.

В повседневной жизни и в научных экспериментах мы никогда не имеем дела с бесконечными десятичными дробями, т.е. с иррациональными вещественными числами. Результаты любых практических действий мы можем выражать только в рациональных числах. Итак, примем в качестве нашей отправной точки поле рациональных чисел Q [2, с. 9].

Нормой называется отображение, обозначаемое через ||-Н, поля F в множество неотрицательных вещественных чисел, такое, что:

• 1)   ||х| = 0 тогда и только тогда, когда

х = 0,

• 2)    Нх^уН = НхН • НуН,

• 3)    Ik + уН < Нх| + НуН [10, с. 9].

Пусть p 6 {2, 3, 5, 7, 11, 13, ...} - некоторое простое число. Для произвольного ненулевого целого числа % (% 6 Z - это множество всех целых чисел) положим ordpx равным кратности вхождения р в разложение х на простые сомножители, т.е. наибольшему целому неотрицательному числу т, для которого х = 0(mod рт). Если х = ^, а, b 6 Z, b Ф 0, то ordpX = ordpa — ordpb [10, с. 10].

Определим на Q (поле рациональных чисел) следующее отображение |-|_р [10, с. 11]:

|х|р = |i

рБ^ , если ^хф 0;

0, если х = 0.

Норма называется неархимедовой, если всегда выполнено неравенство ||х + у| <  тах(^н%^н, ИуЮ [10, с. 11] .

Таким образом, р|р является неархимедовой нормой на поле Q .

Поле Q_p р -адических чисел называется пополнение поля Q рациональных чисел по р -адической норме.

Данное определение есть точный аналог конструкции вещественного числа путем по- полнения поля рациональных чисел по норме, определяемой вещественным расстоянием. В Qp можно ввести метрику (р-адическое расстояние), порожденную р-адической нормой:

с1_р(х,у) = \х —у\_р. Q_p является полным метрическим сепарабельным пространством [10, с. 9].

Таким образом, р -адические числа составляют неотъемлемую часть теории чисел, алгебраической геометрии и других разделов современной математики, применяются в теоретической физике, а также для исследований в области экономики.

Р-адическое моделирование: методика и реализация построения типичных случаев

Р -адическая аппроксимация изменений курсов активов позволяет представить ценовые изменения на финансовых рынках в пространстве р- адических чисел, а не вещественных. Такое представление способствует наиболее точному отображению скачков индексов фондовых бирж, курсов активов, котировок валют [23].

Методика построения р -адической аппроксимации заключается в следующем алгоритме действий [6; 8].

• 1.    Выбор р -адического числа (р = 2, р = 3). Р- адическое число используется для описания корректирующих и импульсных волн.

• 2.    Перевод числа в р -адичную систему исчисления. Любое р -адическое число при переводе из целого числа х по основанию р имеет

• 3.    Построение кусочно-линейной ап-

• проксимации волновых паттернов р-адическими отображениями: yt = у(х) = а + b • х(р).

запись: 0. а₀а 1 а₂ ... а ^ ..., где а ^ £ {0,1,..., р — 1} и х(р) = а₀ + а 1 р ^ 1 + а₂р²' ^ ² +—, где ( 1 , (₂,... е[0,2] - размерность р -адического числа.

Таким образом, р-адическая аппроксимация представляет собой кусочно-линейную модель, параметры которой могут быть найде- ны с помощью метода наименьших квадратов. При этом функция yt зависит от значений не только параметров, но и другой функции х(р). Функция х(р), в свою очередь, определяется значением р-адического числа. Задача нахождения уравнения модели является задачей условной оптимизации (1), решение которой заключается в нахождении уравнения модели

• (2)    при соблюдении ограничений (4) и выпол

нении условия (3) [14 - 16].

S² = (y t ^- Kj}^{2 4} min, t = 1,m,    j = 1, n;

• У^ = а + b- х , (р), j = 1,n;

х ] (р) = а о + Т^а • р¹^¹ ), j = 1,n;

( р = 2 или р = 3,

( i £ [0,2],                              (4)

а ^ ^£ {0,1,... р- 1};

где t - количество исходных точек, j - количе- ство аппроксимирующих р-адических точек.

На основе предложенной методики можно построить р -адические кусочнолинейные модели для наблюдаемых на финансовых рынках элементарных фигур.

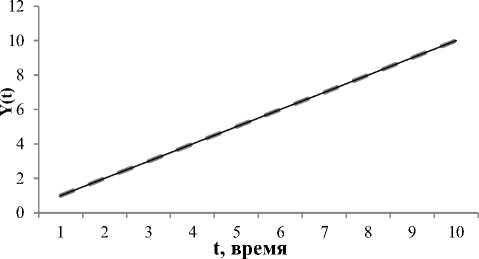
• 1)    Линейная функция, зависящая только от константы y_t j = а + b • х ] (р), где аФ 0, b = 0 (рис. 1). Данная элементарная фигура, для которой погрешность S² = 4,44 • 10^-12 ^ min,    описывается    уравнением

  y tj = 0,998 + 7,36 • 10^{- 7} • (a o, _t + a i, _t + a 2, _t + +a₃ , _t • 2 ³⁰¹⁹⁹ ), t = 1,10, j = 1,10.

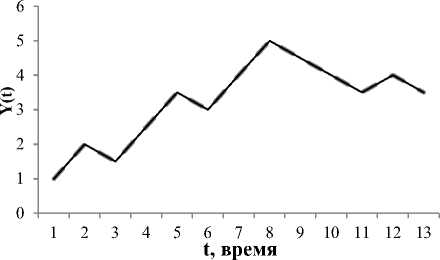
• 2)    Линейная функция, зависящая не только от константы, но и от времени y_t j = а + b • х ] (р), где аФ 0, b Ф 0 (рис. 2). Данная элементарная фигура, для которой погрешность S² = 2,98 • 10^-9 ^ min, описывается уравнением y tj = a o,t + a i,t • 3 ° ⁹" + a 2,t • З ²'⁰⁹⁹⁹ , t = U0,j = ПО.

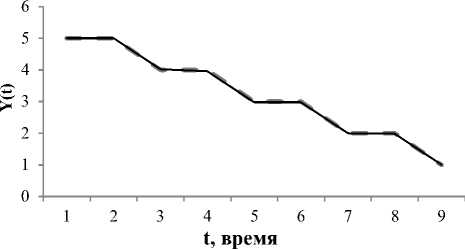
• 3)    Ступенчатая функция (рис. 3). Данная элементарная фигура, для которой погрешность S² = 0,128 ^ min, описывается уравнением y_t j = 5,978 — 0,979 • (a_ot + a_1t • 2⁰ + +a₂ , _t • 2 ²⁰ ,5 ²³ + a₃ , _t • 2³ • ¹ , ⁰¹⁴), t = 19,j = Щ.

• 4)    Волновой цикл Р.Н. Эллиотта (рис. 4). Данная элементарная фигура, для которой погрешность S² = 2,65 • 10^-8 ^ min, описывается двумя уравнениями:

• a)    ft* = 0,999 • ^ + а_и • 3^0,369) , t = 1Ц, к = 111;

• b)    y_til = 9,738 — 0,5 -(O 0,t + а_и • 3 ⁰ + +а₂ ; • 3² • ¹ , ⁰⁶⁹) , t = 9,13, I = 9,13.

Далее, на рис. 1 - 4 приведем графики элементарных фигур (пунктирная линия) и графики моделей (сплошная линия).

1,5

1,3

0,7

0,5 т-------------1-------------1-------------1-------------1-------------1-------------1-------------1-------------1-------------1----------

123456789 10

t, время

“ “ Элементарная фигура -----Модель

Рис. 1. График элементарной фигуры как линейной функции при а = 1 и b = 0

Элементарная фигура          Модель

Рис. 2. График элементарной фигуры как линейной функции при b >0

Элементарная фигура         Модель

Рис. 4. График элементарной фигуры как волнового цикла Р.Н. Эллиотта

Элементарная фигура         Модель

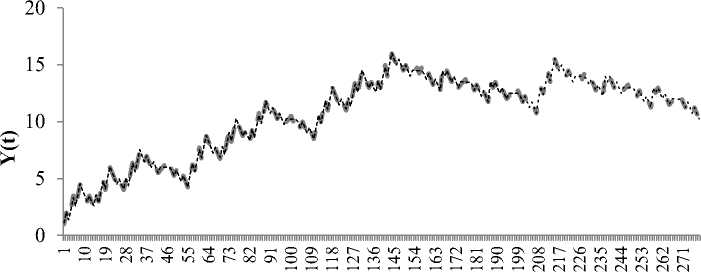
В качестве базисной фигуры изменений курсов активов выступает волновая модель Р.Н. Эллиотта. Данную модель можно представить как фрактал третьего уровня. Если для изучения рыночного цикла Р.Н. Эллиотта взять исходную модель, состоящую из 278 точек, то р -адическая кусочно-линейная аппроксимация будет включать 145 точек и будет записана с использованием четырех функций (рис. 5) [14 - 16].

Рис. 3. График элементарной фигуры как ступенчатой функции

t, время

Исходные данные, фрактал третьего уровня Модель фрактала Рис. 5. Графики фрактала третьего уровня и его модели

Р -адическую кусочно-линейную аппроксимацию фрактала третьего уровня можно представить следующим образом: как решение задачи условной оптимизации – значение целевой функции (5) и уравнение модели при выполнении условий (6).

В математическом пакете Wolfram Mathematica могут быть реализованы команды по построению графиков аппроксимации паттерна р-адическим отображением для финан- сового рынка.

S 2 = 3,472,

• 1)    y^_k = 6,415 + 0,978 • (o o.t + а^ • • 3⁰ , ²⁰⁹), k = 1,8, t = 1. .8,14. .21,27..

  
  
  
  

..34,56..63,69..76,82..89,111..118,124.. . .131,137. .144,208..215;

• 2)    y^i = 48,467 - 0,521 • (a o,t + а_1Л •

• • 3⁰ + a₂ , _t • 3² ' ¹ , ⁹⁶⁹), I = 9,13, t = 9..

..13,22..26,64..68,77..81,119..

..123,132..136;

• 3)    y t, _m = 12,842 - 0,499 • a o,t ,

m = m, t = 35. .42,48..55,90. .97,103. .110,145..

..152,158..165,166..173,179..186,187..

..194,200..207,216..223,229..236,237..

..244,250..257,258..265,271..278;

• 4)    y_t , _n = 14,169 - 0,0267 •

• • (a₀ ,t + a 1, _t • 3 0 + a₂ , _t • 3 2^2 ), n = 9,13, t = 43..47,98. .102,153. .157,174..

. .178,195. .199,224. .228,245. .249,266..

..270.

В пакете Wolfram Mathematica находится функция р- адического числа с использованием стандартных операций: fxp [x_iPp ] := IntegerDigits[x, p]. Table [^{pi ^ ^} \^_ntegerDigits[x, p]] - 1,0, -1}]

Записываются значения р-адического числа, значения параметра р-адического числа и значения коэффициентов в уравнении модели: р = «Значение р-адического числа»;

β = «Значение параметра (показателя степени) р -адического числа»;

• a, b = «Значение коэффициентов в управле-

• нии».

.

Строится график аппроксимации волновых паттернов р -адическими отображениями: у := a + b • fxp[i, p, ^] - линейная зависимость;

ListlinePlot ^Flatten\Table[y, {i, 0,1000}]]].

Результатом выполнения команд явилось построение на основе имеющихся данных (табл. 1) наиболее типичных случаев флуктуаций цен акций на финансовых рынках [14 - 16] с использованием аппроксимации волновых паттернов р -адическим отображением [8]:

• 1)    аппроксимация паттерна «Пила» для изменения цен на акции ПАО «Аэрофлот – российские авиалинии» (рис. 7);

• 2)    аппроксимация паттерна «Флэт» для изменения фьючерса RTSo (рис. 9);

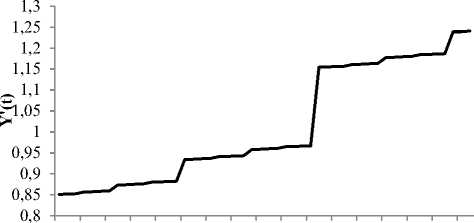
• 3)    аппроксимация паттерна «Лестница» для изменения курсов на ценную бумагу AFKS (рис. 11).

  Таблица 1

  Исходные данные для построения модели изменения курсов активов

  №	Актив	Период моделирования	Таймфрейм
  1	Акция ПАО «Аэрофлот – российские авиалинии» (рис. 6)	01.01.2009 - 27.09.2012	1 неделя
  2	Фьючерс RTSo (рис. 8)	01.01.2014 - 11.02.2014	1 день
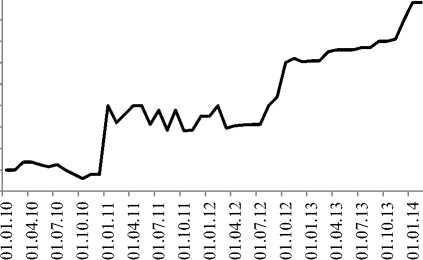
  3	Ценная бумага AFKS (рис. 10)	01.01.2010 - 01.02.2014	1 неделя

  
  
  

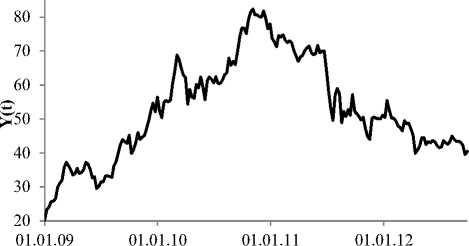
  t, время

  Рис. 6. График реального изменения цен акций ПАО «Аэрофлот – российские авиалинии»

  
  
  

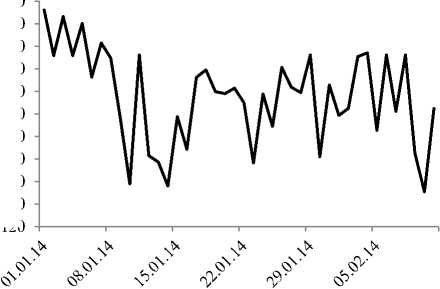
  t, время

  Рис. 8. График реального изменения фьючерса

  
  
  

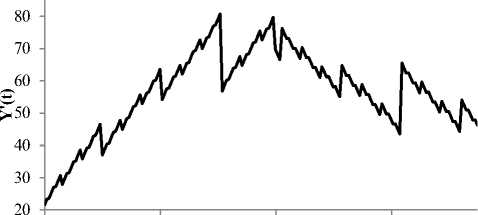
  01.01.09        01.01.10        01.01.11        01.01.12

  t, время

  Рис. 7. Аппроксимация паттерна «Пила» р- адическим отображением

  
  
  

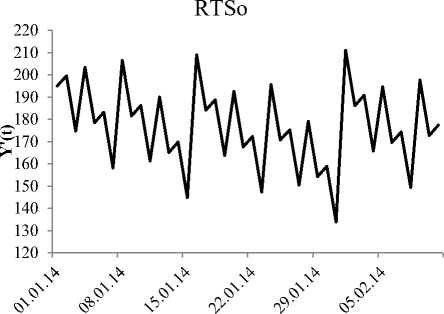
  t, время

  Рис. 9. Аппроксимация паттерна «Флэт» р -адическим отображением

  
  

1,3 1,25

1,2 1,15

1,1 1,05

1 0,95 0,9 0,85 0,8

t, время

Рис. 10. График реального изменения ценной бумаги AFKS

t, время

Рис. 11. Аппроксимация паттерна «Лестница» р -адическим отображением

Таким образом, имеющаяся методика р -адического моделирования сходна с методикой построения регрессионных моделей, а именно: в качестве спецификации модели используются линейные зависимости между параметрами, в качестве оценки модели находится величина погрешности модели от реального графика. Также стоит отметить, что графики моделей ценовых колебаний, полученных на основе применения методики р -адического моделирования, по сравнению с исходными графиками выглядят правдоподобно.

Р-адическая аппроксимация динамики индекса РТС по таймфреймам

Принято считать, что величина доходности индексов фондовых бирж, курсов ак-ций/облигаций, котировок валют масштабноинвариантна [4] и описывается уравнением [1, с. 135] R(At) = lnY(t) — lnY(t — At), где Y - значение курсов активов.

В рамках данной работы авторами исследуется величина доходности индекса РТС (табл. 2), причем интервал времени (At), за которое происходит изменение индекса, выбирается равным месяцу, неделе, дню и часу. Независимо от того, с какой частотой совершаются колебания индекса РТС, все четыре модели состоят из 80 точек, а их прогнозы строятся для 13 точек.

Таблица 2

Исходные данные для построения моделей индекса РТС

" ~—^^^^Индекс РТС Показатель          ——	Индекс РТС (по месяцам)	Индекс РТС (по неделям)	Индекс РТС (по дням)	Индекс РТС (по часам)
Период моделирования	Янв. 2009 – Авг. 2015	15.12.2014 – 20.06.2016	11.05.2016 – 29.07.2016	04.08.2016 (10:00) – 16.08.2016 (17:00)
Период прогнозирования	Сент. 2015 – Сент. 2016	27.06.2016 – 19.09.2016	30.07.2016 – 11.08.2016	16.08.2016 (18:00) – 18.08.2016 (12:00)
Таймфрейм	Месяц	Неделя	День	Час
Количество моделируемых точек	80
Количество прогнозных точек	13

Для моделирования изменения величины доходности с использованием р -адики определяется значение р -адического числа. График доходности представляет собой аппроксимацию паттерна «Флэт», для которого характерны модели с р = 2 [9]. Поэтому в моделях колебания индекса РТС в качестве фактора выбрано р -адическое число, равное двум.

Параметры уравнений (2) и (3) находятся в результате решения задачи условной оптимизации. Минимальным значением погрешности (15, 12) обладает модель индекса РТС, представленная по месяцам. При этом на незначительно большее значение откло- няется модель по дням (значение погрешности равно 22,61).

Для определения корректности модели по полученным уравнениям строятся р -адические прогнозы, которые условно можно разделить на следующие типы:

• 1)    оптимистичный сценарий, когда угол наклона импульсных волн круче, чем у корректирующих. Сценарий представляет собой восходящий («бычий») тренд;

• 2)    пессимистичный сценарий, когда угол наклона корректирующих волн круче, чем у импульсных. Сценарий представляет собой нисходящий («медвежий») тренд;

• 3)    усредненный сценарий, когда прогноз отражает общую (усредненную) тенденцию развития модели на основе исходного количества данных;

• 4)    сценарий продолжающегося развития показывает возможные колебания будущих значений при условии, что динамика последних известных точек не изменится.

Для имеющихся четырех моделей на рис. 12 - 15 построены соответствующие прогнозы.

На основе оценки погрешности построенной модели и минимальной оценки погрешности одного из типов прогнозов можно определить оптимальный торговый период для р -адических исследований. В результате таковым явился таймфрейм, равный дням (табл. 3).

Таблица 3

Оценка погрешности модели и прогнозов для индексов РТС по таймфреймам

—— ^ ^  РТС Показатель	Индекс РТС (по месяцам)	Индекс РТС (по неделям)	Индекс РТС (по дням)	Индекс РТС (по часам)
Погрешность модели	15,12	81,31	22,61	988,67
Погрешность оптимистичного прогноза	1877,32	1092,82	882,60	532,44
Погрешность пессимистичного прогноза	3954,77	4448,54	934,03	585,58
Погрешность усредненного прогноза	1002,25	1026,50	318,25	464,02
Погрешность прогноза продолжающегося развития	2569,66	275,67	310,79	387,25
Минимальная погрешность одного из прогнозов	1002,25	275,67	310,79	387,25

t, время

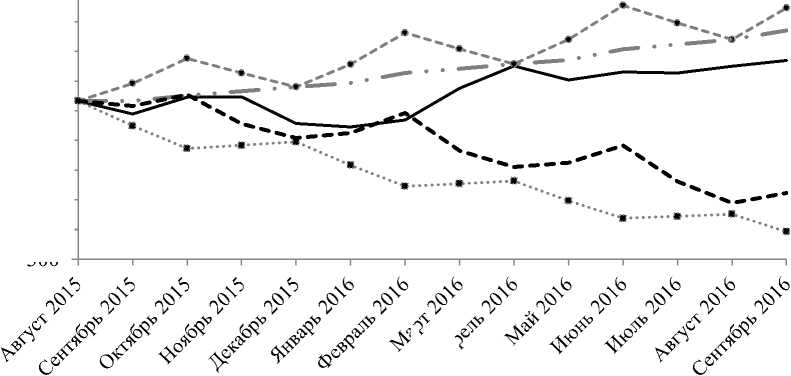
Здесь и далее на рис. 12 - 15:

Исходные данные                                   Р-адический оптимистичный прогноз

Р-адический пессимистичный прогноз                    Р-адический усредненный прогноз

Р-адический прогноз продолжающегося развития

Рис. 12. Графики фактических данных и прогнозов значения индекса РТС по месяцам

^jo X

V V

<о Jo Jo

^ х> ^■

*0 Jo Jo Jo s ^’ t, время

Io Jo Jo Jo Jo Jo

Рис. 13. Графики фактических данных и прогнозов значения индекса РТС по неделям

I© X

V'

J Jo Jo 4

Ф’ ^' ^'

^'

<У

Jo

t, время

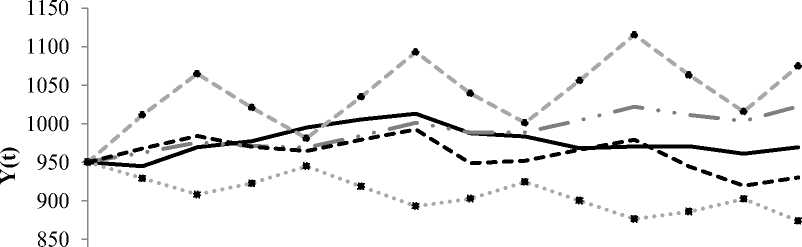
Рис. 14. Графики фактических данных и прогнозов значения индекса РТС по дням

5^

C'

Io kJ kJ t, время

Рис. 15. Графики фактических данных и прогнозов значения индекса РТС по часам

В итоге прогноз колебаний индекса РТС в большинстве случаев (в трех из четырех моделей) наиболее сильно коррелирует со сценарием продолжающегося развития. А пессимистичный сценарий показывает худшие результаты прогнозов.

Заключение

На основании изученных моделей определим преимущества р- адического моделирования. К ним относятся:

• 1.    Упрощенная процедура включения факторов в модель. В качестве факторов

• 2.    В интервал р -адических спрогнозированных значений попадают фактические значения прогноза. Определено, что сценарий продолжающегося развития наиболее точно отражает характер и тенденцию изменений курсов активов.

• 3.    Относительно высокая точность при малом количестве аппроксимирующих точек для небольшого числа значений исходных данных.

р- адической модели выступают р- адические числа, которые не проверяются на мультиколлинеарность, гетероскедастичность и автокорреляцию в остатках.

К недостаткам относятся следующие пункты:

• 1.    Трудоемкий и сложный процесс моделирования паттернов.

• 2.    Прогноз может быть составлен только на краткосрочный период.

Следовательно, р -адическое моделирование позволяет наглядно демонстрировать флуктуации, используя аппроксимацию волновых паттернов р -адических отображений. В свою очередь, р -адическое прогнозирование предоставляет интервал будущих значений и несколько вариантов развития модели.