Параллельное решение упругопластической задачи с применением трехдиагонального алгоритма LU-разложения из библиотеки ScaLAPACK

Упругопластическая задача с большими пластическими деформациями физически и геометрически существенно нелинейна и требует большого количества времени для её решения на персональном компьютере. Например, на решение двумерной задачи методом конечных элементов (МКЭ) на регулярной сетке с одинаковым числом ячеек, равным 200 вдоль каждой из сторон расчетной области, затрачивается несколько часов; для трёхмерной задачи с аналогичной сеткой это время увеличивается до нескольких суток. Существенно сократить время вычислений можно с помощью техники с параллельной архитектурой, в частности, кластерных систем.

Реализация МКЭ в упругопластических задачах осуществляется в условиях пошагового нагружения и на каждом таком шаге состоит из трёх основных этапов [1]: 1) расчёт локальных матриц жёсткости для конечных элементов и формирование матрицы A (глобальной матрицы жёсткости) и вектора b правой части системы линейных алгебраических уравнений (СЛАУ)

Ax = b                                                                      (1)

относительно искомого вектора x обобщённой скорости в узлах конечно-элементной сетки; 2) решение СЛАУ (1);

• 3)    вычисление напряжённо-деформированного состояния конечных элементов в конце шага нагружения.

• 2.    Алгоритмизация параллельного решения СЛАУ

На каждом шаге нагружения этап 1 выполняется один раз, а этапы 2 и 3 — от десяти до пятнадцати раз для удовлетворения итерационно с приемлемой точностью условию пластичности в конце шага нагружения. При этом матрица жёсткости остается постоянной, а изменяется только правая часть системы уравнений. Если этапы 1 и 3 легко распараллеливаются, то алгоритмизация распределённого параллельного решения СЛАУ является сложной задачей.

Матрица A имеет ленточный вид с небольшой относительной шириной ленты. Ширина ленты зависит как от типа аппроксимирующей расчетную область сетки, так и от способа нумерации её узлов и является единственной основной характеристикой матрицы СЛАУ. Для рассматриваемого алгоритма решения системы уравнений в данной работе, с целью упрощения анализа результатов, рассматриваются только регулярные сетки с одинаковым числом ячеек d вдоль каждой из сторон. Для таких сеток отношение полуширины ленты k к размерности n вектора x (к количеству переменных в задаче) для двумерных и трёхмерных задач примерно одинаково и, например, равно 0,01, 0,005 и 0,0033 соответственно для d =100, 200 и 300.

Целью работы является исследование возможностей трёхдиагонального параллельного алгоритма, основанного на LU-разложении матрицы A , при решении СЛАУ в упругопластических задачах на кластерной системе.

Исследуется трёхдиагональный параллельный алгоритм вычисления LU-разложения и решения системы линейных уравнений без выбора ведущего элемента, описанный в работах [2, 3] и реализованный в библиотеке ScaLAPACK [4]. Для решения системы линейных уравнений (1) матрица A разбивается на блоки (см. Рис. 1) и распределяется на p процессоров следующим образом:

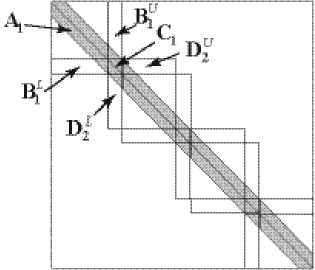
Рис. 1. Разбиение матрицы А на блоки; число блоков p = 4

f A B "

B f C i D "

D LL A ₂ B "

BL

_D L _p

_D U _p

x ₁ ξ 1 x ₂

^ p - i

V x p 7

fb ) в b

e p - 1

V b p 7

где соответственно матрицы A _i и C _i имеют

размерности n x n. и k x k ( i = 1, ..., p ); а векторы

x _i , b _i и ξ _i , β _i — размерности n_i и k ; B ^U _l B _l ^L D ^U _p

D ^L _p — прямоугольные матрицы (соответственно их размерности k x n , n x k , k x n , n_t x k ). Здесь ^ i ,

βi — части вектора, отвечающие i-му блоку матрицы A . Общее число искомых p переменных вычисляется по формуле: ^ ni +(p -1) k = n . Такое трёхдиагональное i=i блочное разбиение возможно только в случае, когда Vi ni > k . Это условие ограничивает предельно возможный уровень параллелизма, а именно максимальное количество процессоров p , которое может быть использовано для параллельного исполнения. При этом должно выполняться условие p < (n + k)/(2k).

Далее матрица подвергается блочно-циклической редукции, то есть переставляются местами строки и столбцы таким образом, что сначала следуют все нечётные из них, а потом все чётные. Получается так называемая чётно-нечётная перестановка

A 2

A

B ₁ ^L D ^U ₂

B 2 ^L

p

LU

(                 p-1 p общей блочной форме fA MUVxL^

( M L C JU) ⁽ в ) .

B 1 ^U

D 2 ^L

C 1

B U ₂

•• B U

_D L _p

C

x ₁

x2

x p x p ξ 1 ξ 2

ξ

)-I

f b , I b ₂

b p b p β 1 β 2

I в p - 1 J

, которую можно записать в более

LU-разложение [5] матрицы системы (2) имеет вид:

AM ^U ( m L C J

₌f L   O lf U L — 1 M U

( m L U ^{- 1} I JI 0 S

,

где L и U — соответственно нижняя и верхняя треугольные матрицы для матрицы A ^ˆ , S = C - M L U - 1 L - 1 M ^U — дополнение Шура [5] для матрицы A , I — единичная матрица.

Дополнение Шура S для матрицы Aˆ представляет собой блочную трёхдиагональную матрицу размерностью ( p -1) х (p -1) с блоками k х к :

S =

f T 1 R 2

V 2 T R 3

^R p - 1

,

R =- d U u ^{- 1} l ^{- 1} b U , V =- B L U ^{- 1} L ^{- 1} D L , i iiii i iiii

T = C- B L U l"b U - d ^ u . , l + , d L , H,..., p Y

Решение системы (2) с учетом разложения (3) распадается на последовательное решение двух систем:

^L . If ^c U^b 1

M ^L U - ¹ I J( Y J ( в J ,

U

L - 1 M ^u S

If ^x

^j( 5 J

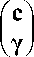
В системах (5) c , и в , — , -е части векторов c и в , вычисляются по формулам c , = L/b ,. , у. = В-В L U 71с. -D U , и-,с ,. I / Г /          /      /     /          / + 1 / + 1 / + , .

Каждый -й процессор независимо от других процессоров вычисляет разложение блока диагонали A , = L , ^. , а также произведения матриц B , ^L U - ¹, L -' B ^u , D U U , - 1 , L -' D ,L , L-'b , и формирует , -ю часть матриц редуцированной системы S^ = y : C , - B ^L U - ¹ L 7¹ B ^u , D U U ^{- 1} L ⁷¹ D L , D^U , 7 ¹ L -¹ B U , B L U ^{- 1} L ⁷¹ D L , в , - B , ^L U , 7 1 c , , D U U , 7 1 c , . Выполнение данных операций не требует межпроцессорных коммуникаций. Для экономии памяти матрицы B ^L U - ¹ , L -' B ^u , D ^U U - ¹ , L-'D ,L и L-'b , помещаются в те же места памяти, которые выделены для матриц B ^L , B ^U , D ^U и D ^L соответственно. Так как в процессе вычислений в матрицах D ^U и D ^L происходит дополнительное заполнение, то требуется дополнительное место в памяти для 2 kn чисел с плавающей точкой. Поэтому общее требование к памяти примерно в два раза больше, чем для последовательного алгоритма. После выполнения локальных вычислений для завершения построения матрицы T согласно (4) процессор с номером i посылает процессору с номером , + 1 матрицу c , - в L u ^{- 1} l⁷¹b U .

Чётно-нечётная перестановка, вычисление разложения и формирование редуцированной системы повторяются до тех пор, пока матрица редуцированной системы не станет заполненной матрицей размерностью k х к . В этом случае получившаяся система может быть решена на одном процессоре. Так как на каждой итерации редукции размерность матрицы уменьшается в два раза, то число шагов, необходимых для достижения желаемого результата, равно целой части от log₂ ( p - 1 ) .

После нахождения векторов ξ _i каждый из процессоров вычисляет свою часть вектора x : x , = I ' ( c , - 1 'B f ^ , ) , x , = U - ¹ ( c , - L'D f $_ - L B % ) , x , = U p '( c , - L D % , - , ) .

• 3.    Результаты вычислительных экспериментов

Все численные эксперименты проводились на решении методом конечных элементов осесимметричной задачи сжатия цилиндра плоскими плитами из упругопластического изотропного и изотропно-упрочняемого материала. В силу симметрии рассматривалась 14 часть продольного сечения цилиндра. Решение основывалось на принципе виртуальной мощности в скоростной форме [1]:

J( о + A t is )**Vh dV + J (P + AtP )*h dZ = 0 V                          Z со следующими определяющими соотношениями, полученными в работе [6]:

i s = X0 1 + 2 ( Х0 + ц ) D -Vv a - о - V v T - J ro S ,

S = о -o ₀ I ,      c ₀ = K 0 ,      K = X + 2/3 ц ,     D = 0,5 ( V v + V v ^T ) ,

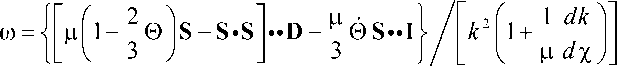
F ( S , к ) = 0,5 S ** S - к ² = 0 — условие текучести Мизеса.                         (6)

Здесь: о — тензор напряжений Коши; P — плотность поверхностных сил; A t — промежуток времени для шага приращения нагрузки; h — вариация кинематически допустимых полей скоростей; V — набла-оператор; V , Z — объем и поверхность цилиндра и их элементы dV , d Z соответственно; X , ц — коэффициенты Ламе; I — единичный тензор; точкой и двумя точками обозначено, соответственно, скалярное и двойное скалярное произведение тензоров; точка над символом обозначает полную производную по времени; V v — градиент скорости перемещений; D — тензор скоростей деформаций; S — девиатор тензора напряжений; а ₀ — среднее нормальное напряжение; K — объёмный модуль упругости; 0 — относительное изменение индивидуального объёма бесконечно малой частицы среды; k — напряжение текучести; J — числовой коэффициент, принимающий значения J = 0 (при F <  0 или при F = 0 , S ** S <  0 ) и J = 1 (при F = 0 , S-S >  0 ); х — параметр упрочнения (в силу малости упругих деформаций X = 2 D •• D ); го — пластический модуль, который вычисляется итерационно для удовлетворения равенства (6) в конце каждого шага нагружения. Опыт вычислений показал, что данное условие с приемлемой точностью выполняется после 10–15 итераций.

На контакте с плитой предполагалось выполнение закона трения Кулона T = -у |P„ |i, где T и Pn — соответственно касательная составляющая и модуль нормальной составляющей вектора напряжений на контактной поверхности цилиндра; i — единичный касательный вектор к контактной поверхности цилиндра, направленный вдоль его радиуса; у — коэффициент трения (в расчетах считался равным у = 0,1, чтобы исключить, с целью упрощения алгоритма решения задачи, переход свободной поверхности на контакт с плитой). Нагружение в виде перемещения плиты осуществлялось ступенчато с шагом Ah . Шаг Ah выбирался так, чтобы отношение Ah/h (h — высота цилиндра) не превышало предел упругости по деформации, в нашем случае — 0,002, что обеспечивало устойчивость вычислительной процедуры. Величина относительного сжатия цилиндра принималась равной 0,5.

Вычисления проводились на кластере um64 Института математики и механики УрО РАН, состоящем из 32 двухпроцессорных двухъядерных модулей на базе процессоров AMD Operton с тактовой частотой 2,6 ГГц. Использовался интерфейс передачи сообщений из библиотеки OpenMPI версии 1.3.3 на сети InfiniBand. Параллельное решение СЛАУ по описанному выше алгоритму было осуществлено с помощью библиотеки ScaLAPACK, реализованной в Intel MKL [] версии 10.0.010. Конечно-элементные сетки имели параметры, представленные в таблице 1.

Таблица 1. Параметры сеток в вычислительных экспериментах

Число ячеек по высоте цилиндра d	Полуширина ленты матрицы СЛАУ k	Число неизвестных n	kn
70	145	10082	0,0144
100	205	20402	0,0100
120	245	29282	0,0084
150	305	45602	0,0067
200	405	80802	0,0050
300	605	181202	0,0033

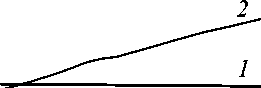
На рисунке 2 приведены доли времени T , приходящиеся на вычисления отдельного этапа в пределах одного шага нагружения при решении задачи на одном процессоре с использованием метода LU-разложения для решения СЛАУ. Видно, что доля времени на решение СЛАУ увеличивается с ростом параметра разбиения d и на мелких сетках занимает почти половину общего времени расчётов на шаге нагружения.

T 0,8

0,6

0,4

0,2

020406080100 d

Рис. 2. Доли времени Т осуществления этапов решения на одном шаге нагружения в задаче сжатия цилиндра: формирование матрицы жёсткости А (кривая 1 ), решение СЛАУ ( 2 ), вычисление напряжённо-деформированного состояния в конечных элементах в конце шага нагружения ( 3 )

Рисунок 3 демонстрирует характер поведения и величину коэффициента ускорения a_p при распараллеливании различных этапов решения упругопластической задачи сжатия цилиндра. Здесь и далее коэффициент ускорения есть a p = t 1 j t p , где t 1 и t p — соответственно время выполнения последовательного алгоритма на одном процессоре и параллельного алгоритма на многопроцессорной вычислительной системе с числом процессоров p >  1.

Значения ap при распараллеливании этапа формирования матрицы жёсткости A представлены на рисунке 3, а. На сетке с параметром разбиения d = 300 время формирования матрицы жёсткости с использованием только одного процессора получено путём экстраполяции результатов, так как для осуществления вычислений на одном узле вычислительной системы не хватало оперативной памяти процессора. Приведённые данные свидетельствуют об эффективности распараллеливания этого этапа. Видно, что ускорение при увеличении количества процессоров практически не зависит от размера сетки .

Рисунок 3, б содержит зависимости коэффициента ускорения a_p от числа задействованных процессоров при распараллеливании этапа вычисления напряжённо-деформированного состояния конечных элементов в конце шага нагружения на p процессорах. Графики показывают хорошую эффективность распараллеливания данного этапа вычислений. Она выше, чем на этапе формирования матрицы жёсткости. Так же, как и на этапе формирования матрицы жёсткости, зависимость коэффициента ускорения от размеров сетки не наблюдается.

Коэффициент ускорения a_p , соответствующий этапу параллельных вычислений LU-разложения (5) матрицы A системы (1), представлен на рисунке 3, в . Видно, что ускорение вычислений при распараллеливании появляется на сетках с параметром разбиения d >  100. При меньшем d происходит замедление вычислений за счёт того, что время на передачу данных превышает время, непосредственно затрачиваемое на вычисление на процессорах. Излом кривых при переходе на число процессоров больше двух получается из-за того, что объём вычислений в параллельном алгоритме примерно в 2 раза больше, чем в последовательном, а также прибавляются дополнительные затраты на передачу данных по сети. С увеличением количества разбиений уменьшается относительная ширина ленты матрицы А , и коэффициент ускорения становится больше 1. Его величина тем больше, чем больше количество разбиений сетки, однако для сравнительно небольших сеток рост коэффициента ускорения замедляется с увеличением количества процессоров.

На рисунке 3, г приведены значения коэффициента ускорения a_p при распараллеливании решения системы (5). Видно, что при всех рассматриваемых значениях параметра разбиения сетки происходит замедление решения данной системы с ростом числа процессоров, и чем больше значение параметра сетки d , тем меньше скорость замедления.

В таблице 2 представлены значения времени, затрачиваемого на одно решение системы (5). Несмотря на то, что ускорение расчетов не наблюдается даже на сетках с параметром разбиения d = 200, время, затрачиваемое на решение системы при одном и том же числе процессоров, мало меняется с увеличением размера задачи (параметра разбиения сетки d ). Это свидетельствует о том, что практически всё время, которое тратится на решение системы уравнений (5), определяется задержкой сети.

Таблица 2. Время, затрачиваемое на однократное решение системы (5)

Параметр разбиения d	Количество процессоров p
	1	2	4	8	16	32	64
	Время, мс
70	12,6	264,7	494,5	757,3	1112,1	1475,4
100	33,8	281,4	539,3	762,2	1083,2	1526,5
120	57,0	273,3	557,0	786,6	1138,3	2076,8
150	127,3	331,2	569,4	787,6	1108,4	1495,1	1886,6
200	250,3	418,6	664,3	874,4	1183,7	1549,2	1919,9
300		832,7	1076,7	1231,2	1471,0	1794,2	2117,1

Рисунок 3, д демонстрирует зависимости коэффициента ускорения решения СЛАУ (1) при распараллеливании на шаге нагружения, когда используется LU-разложение матрицы системы A и решение системы (5). До тех пор, пока не выполнилось условие пластичности, система (5) в рамках упругопластической задачи, решалась 15 раз. При этом матрицы L и U оставались постоянными, а изменялась только правая часть матрицы B .

Видно, что при наличии ускорения для LU-разложения матрицы A (см. Рис.3, в ) и его отсутствии при решении системы (5) (см. Рис. 3, г ) в сумме ускорение проявляется на сетках с параметром разбиения d = 200 . Это объясняется тем, что время решения системы (5) даже при большом количестве уравнений на несколько порядков меньше, чем время, затрачиваемое на LU-разложение матрицы, поэтому в итоге при распараллеливании вычислений выигрыш во времени наблюдается. Поскольку объём арифметических операций для LU-разложения есть асимптотически самая большая величина в решаемой задаче, то при дальнейшем увеличении количества разбиений сетки ускорение будет иметь место.

Полученные значения коэффициента ускорения a_p при распараллеливании решения всей упругопластической задачи в зависимости от количества используемых процессоров p и параметра разбиения сетки d показаны на рисунке 4. Видно, что для сеток с параметром d >  150 при количестве процессоров больше 4 коэффициент ускорения больше 1.

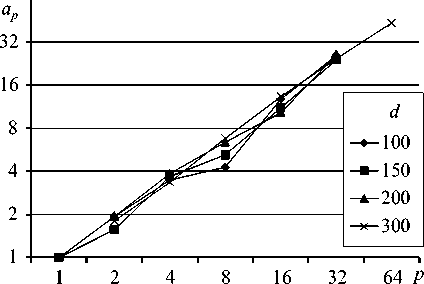
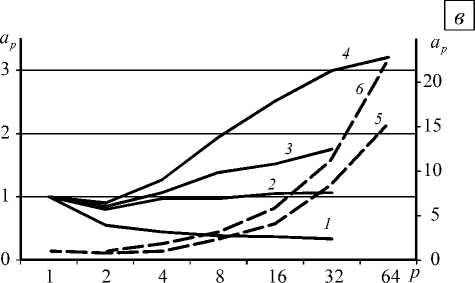
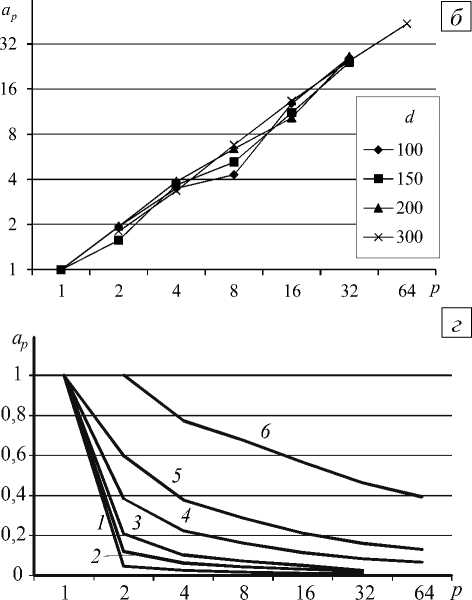
Рис. 3. Зависимости коэффициента ускорения a_p при распараллеливании этапа построения матрицы жёсткости ( а ), вычисления напряжённо-деформированного состояния конечных элементов ( б ), выполнения LU-разложения матрицы СЛАУ ( в ), решения системы (5) ( г ), решения СЛАУ (1) ( д ) от числа процессоров p при различных значениях параметра разбиения сетки d : 70 (кривая 1 ), 100 ( 2 ), 120 ( 3 ), 150 ( 4 ), 200 ( 5 ), 300 ( 6 ); на фрагментах ( в ) и ( д ) кривым 5 и 6 отвечает шкала справа

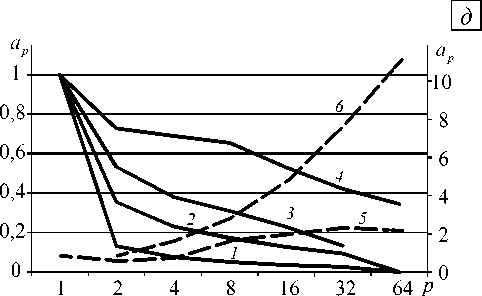
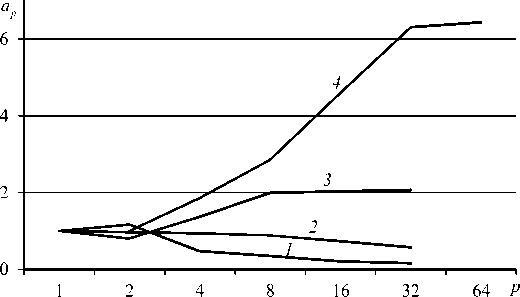
Рис. 4. Зависимости коэффициента ускорения a_p при распараллеливании всего решения упругопластической задачи от количества используемых процессоров p при различных значениях параметра разбиения сетки d : 100 (кривая 1 ), 150 ( 2 ), 200 ( 3 ), 300 ( 4 )

Ускорение на двух процессорах для сетки с параметром разбиения d = 100 объясняется тем, что проигрыш во времени, связанный с вычислениями при использовании параллельного алгоритма LU-разложения, компенсируется выигрышем, полученным в результате распараллеливания расчёта напряженно-деформированного состояния. На сетке с параметром разбиения d = 150 эти значения компенсируют друг друга, поэтому ускорения не происходит. Затухание роста коэффициента ускорения, наблюдаемое на больших сетках, имеет место тогда, когда время, затрачиваемое на вычисление LU-разложения, становится одного порядка со временем, затрачиваемым на нахождение решения СЛАУ.

• 4.    Заключение

  При решении упругопластической задачи методом конечных элементов основное время затрачивается на решение СЛАУ. Так как матрица системы ленточная, и относительная ширина ленты уменьшается при увеличении количества разбиений конечно-элементной сетки, то рассмотренный в работе параллельный алгоритм решения СЛАУ можно использовать для решения упругопластических задач с параметрами регулярной сетки k[n <  0,0067.

Работа выполнена в рамках программы Президиума РАН «Интеллектуальные информационные технологии, математическое моделирование, системный анализ и автоматизация».