Параметрическая идентификация квазилинейного разностного уравнения

Проблема идентификации является в настоящее время одной из основных проблем системного анализа и его приложений в различных областях [1]. При идентификации предполагается экспериментальное изучение и сопоставление входных и выходных процессов, а задача идентификации состоит в выборе соответствующей математической модели. Модель должна быть такой, что ее реакция и реакция объекта на один и тот же входной сигнал должны быть, в известном смысле, близкими. Поиск модели, как правило, ведется в параметризованных классах, полученных «на основе физических закономерностей и представлений о процессах». Одним из таких классов является класс квазилинейных разностных уравнений. В качестве примеров можно привести:

• •    модели делового цикла [2]:

Y ^- Y - 1 = u t + ^S ( Y - 1 ^- Y - 2 ^{) +} v ( Y - 1 ^- Y - 2 ) , где Y - доход в момент времени t, u_t - налоги (экзогенная переменная), v , s - параметры модели;

• •    модели оценки влияния различных факторов рыночной среды на процессы переноса (трансфера) и освоения инновационных (в том числе информационных) технологий [3]:

dy

— = u (t) + ay (t) + by , dt где y(t) - объём распространения инновации к моменту t; экзогенная функция u(t) и параметры а, b модели отражают суммарное число потенциальных потребителей инновационного продукта на рынке, степень внешних (влияние СМИ, рекламы, публикаций) и внутренних воздействий (непосредственное общение людей) на скорость адаптации;

• •    и др. [4].

Как правило, все подобные модели имеют параметры, являющиеся коэффициентами систем интегро-дифференциальных уравнений. В данном случае исходная проблема идентификации может быть сведена к задаче идентификации коэффициентов разностного уравнения, т. е. к оценке их значений по наблюдаемым возмущенным траекториям. Такой подход правомерен при наличии большого объема априорной информации об искомых параметрах и при несоответствии реальных параметров принятой модели приводит к потере сходимости алгоритма.

В данной работе показано, что идентификация квазилинейного разностного уравнения сводится к задаче регрессионного анализа с взаимно зависимыми наблюдаемыми переменными. В первом разделе задача идентификации квазилинейного уравнения представлена в виде задачи ОМНМ-оценивания [5, 6], которая в соответствии с [7] может быть решена с помощью решения последовательности задач ВМНМ-оценивания, представляющих задачи кусочно-линейного программирования. В третьем разделе подробно рассмотрена задача ВМНМ-оценивания. Показано, что ее решение сводится к задаче линейного программирования (ЛП) простой структуры. Простота структуры допустимого множества используемой задачи ЛП: пересечение линейного подпространства с параллелепипедом, – позволяет предложить эффективный алгоритм ее решения, основанный на методе проекции градиента [8, 9]. Описание алгоритма и доказательство его результативности приведено в разделе 4.

Постановка задачи

Пусть {yt е R}M_m+i - значения переменных состояния (т. е. эндогенных переменных) в моменты времени t еM . Пусть {xtрxt2,.,xtn еR}M=x - значения переменных управления (т. е. экзогенных переменных) в моменты времени t е M . Пусть g^: Rm ^ R, j = 1,2,. m - заданные функции, {^ е R}M=x - случайные ошибки. В статье рассматривается проблема определения неизвестных коэффициентов ax, а2, а3., ат е R, Ъх,Ъ2,b.,Ьп е R квазилинейной модели авторегрессии y. =Еajgj{у.-k}m=i +Zbjxtj + et, t=1»2».»M.

j=1

Введем новые обозначения с целью уменьшения громоздкости математических выражений

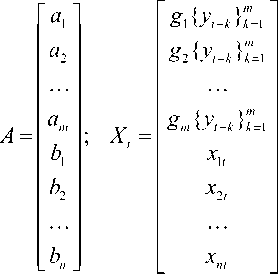
; t = 1,2, . , M ; N = n + m.

В новых терминах задача (1) примет вид yt = ATXt + 6t, t = 1,2,.,M.(2)

Наиболее известным методом определения коэффициентов уравнения регрессии является метод наименьших квадратов (МНК)

T

A= argmiN Я AX. - y.) , который является параметрическим методом, требующим выполнения ряда строгих ограничений: детерминированности переменных, независимости и нормальности распределения погрешностей измерений [10–12]. Даже незначительные нарушения этих предпосылок резко снижают эффективность оценок МНК [13, 14].

Если допустить погрешности в измеренных значениях эндогенных переменных yt, t = 1,2,.,T), то их наличие в значениях функций gy{yt_^}^=1 очевидно. Кроме того, эти ошибки будут взаимно коррелированы и иметь распределения вероятностей, отличные от нормального распределения. Это делает неэффективными классические схемы решения, основанные на методе наименьших квадратов и его вариациях.

Нахождение оценок коэффициентов уравнения авторегрессии существенно осложняется плохой обусловленностью системы уравнений, представляющих собой необходимые условия минимума суммы квадратов отклонений, при этом оценки становятся несостоятельными.

Альтернативой МНК является метод наименьших модулей (МНМ) [15, 16].

M

A = ^mn Я A ^T X- - у- I                         ⁽⁴⁾

Возможными обобщениями МНМ являются взвешенный МНМ (ВМНМ)

А* = arg¹^ Я ( P - A T X, - У - |), P - е^R,   - = 1,2, . M

и обобщенный МНМ (ОМНМ)

M

A=argm"in Я p(l AT X-- у-1), где р(*) - выпуклая вверх дифференцируемая функция.

Основной проблемой при применении ВМНМ является отсутствие общих формальных правил выбора весовых коэффициентов. Идентификация квазилинейного уравнения (1) авторегрессии возможна применением ОМНМ с использованием установленной связи между ОМНМ- и ВМНМ-моделями [7], позволяющей решить проблему определения ОМНМ-оценок посредством итеративной процедуры ОМНМ-оценивания с ВМНМ-оценками [5, 6].

Проблема ВМНМ оценивания

Алгоритм ВМНМ-оценивания для задачи (5) приводит к решению задачи кусочно-линейного программирования

M

Я P - A ^T X - ^- y - | ^ mill,                                  ⁽⁷⁾

i = 1

для заданных X_t е R N , у , p_t е R, - = 1,2, . M . Задача (7) эквивалентна задаче линейного программирования

M

Ep,z, ^ min ,(8)

‘     AeRN, z■M

ATX- + z- >у-,   - = 1,2,.,M,(9)

• -    AT X + z >- у,  - = 1,2,., M.(10)

Двойственной задаче (8)-(10) является задача

M

Я( u- V)у- ^ max, и, ve<

M

ЯХДu- -v-) = 0,  j = 1,2,.,N,(12)

i=- u- + V- = P-, i = 1,2,_, M,(13)

ut,v >0,   i = 1,2,...,M.(14)

Введем переменные w_t = u_t - v_t , - = 1,2, . , M . Из условий (13)-(14) следует

Pt + W       Pt - Wt u =  ----L, v =  ----L,  - = 1,2,.,M.

• -        2         -2

• - p - <  w - < p - , - = 1,2, . , M .

Поэтому оптимальное значение задачи (11)-(14) равно оптимальному значению задачи

M

E w • у ^ max, w eR ^M

^Х^ = 0,   j = 1,2,..., N ,                            (16)

t = 1

- p_t <  W t < Pt ,    t = 1,2,..., M.                                 (17)

Если w* является оптимальным решением задачи (15)-(17), то оптимальное решение задачи (11)-(14) равно

*   P, + W*    * р, - w*

• и, = ^---- ^L,   v, = t^ ----^L, t = 1,2,..., M .

t        2         t2

Из условия комплементарности для пары взаимно двойственных задач (8)-(10) и (11)-(14) следует

(A*)T X, = у,,   t: - pt < w* < p,,(18)

z;=| .     °. ,           =c™ |w^

^w* (y_t - (A ) X), в противном случае ,

Фактически (A, z*) является оптимальным двойственным решением задачи (15)-(17).

Повышение эффективности алгоритма ВМНМ-оценивания

Известен точный алгоритм МНМ-оценивания [17]. Этот алгоритм имеет вычислительную сложность O(M²N²+ M⁴Nlog N + M²Nlog²N) . Кусочно-линейная форма целевой функции и простая структура допустимого множества задачи (15)-(17) дает основание полагаться на возможность ее более эффективного решения задачи. Решения таких задач, как (15)-(17), возможны с помощью алгоритма, основанного на методе проекции градиента [8, 9]. В рассматриваемом здесь случае, благодаря простоте структуры допустимого множества, вычислительная сложность алгоритма не превышает величины O(M²N²) .

Алгоритм PrGrad

Вход:     X е RN хRM, р e(R⁺)M , y е RM.

M

Выход:   w* = arg max V w. • y..

welm “ i г =1

Шаг 1. /* Инициализация*/

Шаг 1.1. k = 0 /* Счетчик итераций */

Шаг 1.2. w⁽⁰⁾ = {^и/° = 0}_z=i ₂м /* Координаты начальной точки */

Шаг 2. /* Текущая итерация к */

Шаг 2.1. Вычислить набор индексов ненасыщенных переменных:

5^(k) = {i: - p_t< w(^k) < pj = 1,2,_, M}.

Шаг 2.2. Вычислить подматрицы ненасыщенных переменных:

X^(k) = {X_jV: i е 5^(k), j = 1,2,_N},  y^(k) = {y; i e 5^(k)}.

Шаг 2.3. Вычислить матрицу проектирования

р⁽k) = e _ x⁽k^)T^x⁽k) x⁽k^)T^ ¹x⁽k)

и проекцию градиента целевой функции g^(k) = P^(k)y^(k).

Шаг 2.4. Проверить необходимое и достаточное условие максимума:

если g^(k) = 0, то перейти на Шаг 3.

Шаг 2.5. Вычислить максимально допустимую длину шага в направлении g^(k): а = argmax {а:-p_t< w^(k) + ag^(k) <p_t,ie5^(k)}. a

Шаг 2.6. Вычислить следующую точку

(k+1) _ _Л.1 k)           (k)       .    _Q(k)

wi    = wi  + a* gi , г e 5   .

Шаг 2.7. Положить k = k +1 и перейти на Шаг 2.1.

Шаг 3. Завершение алгоритма: w* = w^(k).

Конец описания алгоритма PrGrad

Теорема. Алгоритм PrGrad корректно решает проблему (15)–(17). Его вычислительная сложность не превышает величины O(M²N²).

Доказательство. Каждая k-я итерация алгоритма состоит из допустимого перемещения из текущей точки w⁽k) в следующую точку w⁽k⁺¹⁾ (см. Шаг 2.6) в направлении проекции g⁽k) градиента y целевой функции (15) на пересечение множества решений системы уравнений (16) и множества решения системы активных ограничений из (17), которые могут быть определены множеством r^(k) = {I: |W⁽K)| = p_t} насыщенных переменных.

Более того, если выполнено необходимое условие для экстремума, т. е. из g^(k) = 0, то для всех i е R^(k) выполняются условия w"^k)y > 0 . Поэтому градиент у не может быть представлен как неотрицательная линейная комбинация градиентов (т. е. внутренних нормалей) активных ограничений. Поэтому в нашем случае в соответствии с теоремой Куна–Такера необходимое условие экстремума также является достаточным, и тело шага 2 будет выполнено не более чем N раз.

Вычислительная сложность шагов 2.1, 2.4–2.6 не превышает величины O(M).

Матрица X^(k) имеет N строк и не более M столбцов. Поэтому вычислительная сложность шага 2.2 не будет превышать O (MN).

Опишем более подробно оценку вычислительной сложности шага 2.3. Вычислительная сложность умножения (N х M) -матрицы на (M х N) -матрицу, т. е. вычисление матрицы в квадратных скобках, не превышает величины O(MN²). Сложность полученной обратной (N х N) -матрицы не превышает значения O(N³).

Вычислительная сложность умножения (M х N) -матрицы на (N х N) -матрицу не превышает O(MN²). Вычислительная сложность умножения (M х N) -матрицы на (N х M) -матрицу также не превышает значения O(MN²).

Таким образом, вычислительная сложность тела цикла не превышает O(MN²+ N³), а вычислительная сложность алгоритма не превышает O(M²N²), поскольку M > N.

Теорема доказана.

Заключение

Идентификация квазилинейного уравнения (1) авторегрессии порядка m, имеющего n экзогенных переменных, по M отсчетам траектории возможна применением ОМНМ на основе связи между ОМНМ- и ВМНМ-моделями, позволяющей решить проблему определения ОМНМ-оценок посредством итеративной процедуры ОМНМ-оценивания с ВМНМ-оценками. При этом задача ВМНМ-оценивания представляет задачу линейного программирования, содержащую N = n + m переменных и 2M ограничений. С помощью предложенного алгоритма PrGrad данная задача решается за время не превосходящее O(M²N²).