Параметрическая идентификация модели механизма с параллельными кинематическими цепями

Построение технологического оборудования на основе механизмов с параллельными кинематическими цепями (МПКЦ) и управление таким оборудованием предполагает использование кинематических моделей МПКЦ [1, 2]. Идеализированная кинематическая модель МПКЦ не в полной мере будет отражать кинематические свойства построенного на его основе оборудования. В частности, это связано с несоответствием геометрических размеров элементов модели МПКЦ и соответствующих элементов реального оборудования. Следовательно, возникает необходимость в экспериментальном уточнении геометрических параметров модели МПКЦ, т. е. требуется выполнить параметрическую идентификацию модели.

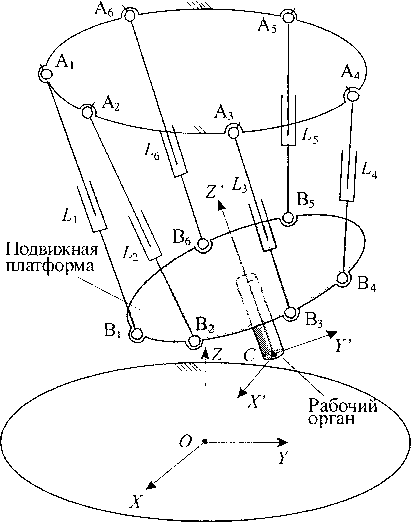
Рассмотрим МПКЦ (рис. 1). Данный механизм включает в себя подвижную платформу, связанную с основанием шестью штангами, имеющими длины Lj , у = 1,6 . Длины штанг могут меняться; примем величины Z_y в качестве входных координат МПКЦ. Выходным звеном МПКЦ является подвижная платформа; в качестве выходных координат механизма целесообразно принять величины, определяющие пространственную ориентацию подвижной платформы как твердого тела.

Свяжем с подвижной платформой некоторый рабочий орган. Пространственная ориентация рабочего органа, а значит, и подвижной платформы, определяется тремя линейными координатами некоторой характерной точки (например, точки С ) в связанной с основанием системе координат (СК) OXYZ и тремя угловыми координатами, определяющими разворот осей связанной с рабочим органом СК CX’Y'Z' относительно СК OXYZ.

Рассматриваемый механизм относится к классу гексаподов и имеет шесть степеней подвижности.

Кинематическая модель МПКЦ, показанного на рис. 1, сводится к следующей системе нелинейных уравнений [3]:

^L?⁼ ^А, ~ ^Ву - ЧУ By - 4^Z\ -^_C)²+ C^Ay - "Vfiy -"VBy ""^By -Ус)²+                _i

+ (% - "l^By -«2 J^By -»3ZBy "^T Л = Ч 6, где (xA ,yA^, zA ) - координаты карданового шарнира, связывающего/-ю штангу с основанием, в

Расчет и конструирование

СК OXYZ; (У_в^ ,Ув₇ ’^zb₇) “ координаты сферического шарнира, связывающего у-ю штангу с подвижной платформой, в СК CX'Y'Z'; (x_c,y_c,z_c) - координаты характерной точки С в СК OXYZ.

\Xx\X

Рис. 1. МКПЦ, имеющий 6 степеней подвижности

Направляющие косинусы 1_к, т_к, п_к. к = 1,3 , входящие в уравнения (1), определяют разворот осей связанной с рабочим органом СК CX'Y'Z' относительно СК OXYZ. Данные направляющие косинусы целесообразно выразить через три угла, описывающих переход от СК OXYZ к СК CX'Y'Z’ путем последовательных поворотов. В качестве этих углов могут выступать углы Крылова ^ , S, у [4]. В этом случае

I_x = cos у/ cos/ + sinSsin^ sin/ ; Z₂ = sin у/ cos 9 ; Z₃ = -cos^sin/ + sin^sinScos/ ;

m_x-- sin у/ cos / + sin <9 cos ^ sin / ; m₂ - cos ^ cos 9 ; m₃ = sin у/ sin / + cos у/ sin 9 cos / ;    (2)

nx = cos S sin/; n^ = -sinS ; n3 = cos Seos/ и кинематическая модель (1) может быть переписана в следующем виде [3]:

С = А, + У% + ^'в, + Uc -% )² + (Ус -У^ )² + <²с -² к, )² +

+2^(Сх|/ Су+ S\|/ S3 Sy)x'B^ + 8\|/СЗ^'в^ + (Sx|/S3Cy-C\|/Sy)z'B^ ^хс -хА^ ) +

+2^(С\|/ S3 Sy-Siy Су)*'^ + СхуСЗу^ + (S\|/Sy + Cv|/S3Cy)z'B, ^j^c ) +

+2^C3 Sy%'B,-S3/B, + C3Cyz'B^zc -zAJ,/ = l, 6, где для сокращения записи введены обозначения: S ^ = sin^/, Су/ - cos^ и т. д.

В качестве параметров кинематической модели, требующих уточнения применительно к реальному МПКЦ, лежащему в основе технологического оборудования, выступают:

• -    координаты кардановых шарниров (т_А^, y_Kj ^^z^^ j ™V^ в неподвижной СК OXYZ;

• -    координаты сферических шарниров (х’_в,, y'_Bj, z'_B^ ) , у = 1,6 в связанной с подвижной платформой СК CX'Y'Z';

• -    длины штанг L^ , у = 1, 6, соответствующих некоторому произвольному положению подвижной платформы, принятому за начальное (нулевое).

Смирнов В.А.                           Параметрическая идентификация модели механизмас параллельными кинематическими цепями

Общее количество подлежащих уточнению параметров - 42. Следовательно, определение этих параметров возможно из 42 независимых уравнений.

Точное знание этих величин позволит определять текущие значения входных и выходных координат МПКЦ. Текущие входные координаты определяются через М^, формируемые при управлении оборудованием:

известные приращения

^=^0>+^;

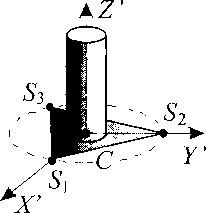
Рис. 2. Метрологическая оснастка

текущие выходные координаты рассчитываются с использованием уравнений (2) - решается прямая задача кинематики о положениях.

Для определения указанных параметров воспользуемся метрологической оснасткой (рис. 2), имеющей элемент крепления к подвижной платформе и тонкую пластину, выполненную в форме равностороннего треугольника. После установки метрологической оснастки на подвижную платформу связанная с оснасткой СК CX'Y’Z' будет полностью определять пространственную ориентацию подвижной платформы.

Пусть МПКЦ находится в начальном (нулевом) состоянии. При этом состоянии механизма могут быть измерены координаты (xs ,ys , zs ), £ = 1,3 вершин Sk треугольной пластины метрологической оснастки, что позволит определить координаты характерной точки С как точки пересечения высот треугольной пластины:

^хс = |щ ^{+ x}s₂ + ^xs₃L Ус ⁼ ^Щ ⁺У$2 ⁺ У$У ^zc =|(^ZS, ^{+ z}s₂^{+ z}s₃)-                (4)

Так как координаты (Xs^y’s^ z’_Sk) точек S_k в СК CX'Y'Z' известны, а пересчет этих координат в СК OXYZ осуществляется с использованием матричного преобразования

=№₇’^V%,*'b₇ ,у\ >^z’_Bj ,x^\y^\z^\y^<0\S^<0\y^          (5)

в качестве неизвестных будут присутствовать только перечисленные выше подлежащие уточнению параметры.

Изменим длину одной из штанг (для определенности первой) на известную величину АД^Х> . В этом случае можно записать следующую систему уравнения:

^ = /1 (^А, > J%, ² А, > ^В, ’ Уб] > ^В, ^ >  У С ^> > ^ZC ^> ^ ^<Ь >                J

Lj<0> = fj (xAj,yKj, z^,x'B?,yBj, z’Bj,x^,y^, z^A>,y,S4>,y\j = ^.,6, где функции /7 определяются уравнениями (3) кинематической модели.

Измерение для данного состояния МПКЦ координат (x_Sk,y_Sk, z_Sk), k-\3 и определение по результатам этих измерений значений выходных координат х^^у^. Zq\\ij^\-9 ,у^<х> позволит использовать шесть уравнений (4) при расчете подлежащих уточнению параметров.

Так как для определения 42 подлежащих уточнению параметров модели МПКЦ требуется 42 уравнения, то системы уравнений (4) и (5) должны быть дополнены еще 30 уравнениями. Требуемые уравнения могут быть получены при последовательном изменении длин штанг:

• -    на величину ХЕ^ изменяется длина второй штанги, тогда

Расчет и конструирование

bL^ = fAxAx,yAx,zAx,x'Bx,VBx,z'^^^

ЬЬ^ = МхАг,уАг,2Аг,х'Вг,УВг,^^

L_J^<°^>=/'_J(x_Aj,y_Aj,z_Aj,x'_Bj ,У_Ву ,^ ,^²\^,.с^2>^^<2>^^<2\у^<2>),7=^;

• -    на величину А^з^3> изменяется длина третьей штанги, тогда

M^f^y^z^x’^y^z’^x^^^

^2   ⁼ /2(^2 'Ук_г ’^za₂ ’^'вг ’Ув₂ ’ ^z'b₂ ’^хс ’Ус ’^zc ’V ^ ’У )~ ^2 ’

\ЬУ3> = МхА ,уА ,zA ,х' ,у' ,z' ,x>3>,y"3>,z>3>,V<3>,9<3>,y<3>)-Lt0>;

U^0> ^/^Уа^а^'в, >Ув, ^\ ^’Г ^с" ’V^<3>’S^<3>,₇^<3>\ j = 4,6

ИТ. д.

В результате будут получены 42 нелинейных уравнения, которые можно сгруппировать в шесть систем по семь уравнений:

J\ ^Ai ^^ZX_x ’^X Bj ⁹ У B! ^{9 Z} B_} ^C ^Ус ^^ZC 4У        ^Y ) Ц

• ^<    Ш_А ,y_A ,z_A ,x' ,У_В ,z' ,х>^к\у>^к>,г>^к>,и/^<к>,£^<к\г^<к>)-Ь^ =^^^ k = l^,

• _<    /2(^A₂ >Уа₂,^za₂>*'b₂ ,У b₂ >²'b₂ ,У"^;УЛ-'У У^^^^{\7^)" A^^^^       z = 0J;}

^x^y^z^x^y^z^y^z^^^         k^

Уб^х_Аб,у_Аб,г_Аб,х'_Вб ,У_Вб ,^в₆ ’X^^^^^,^,^^}-^ =0, z = 0,5;

[/6(хАб,уАб,;Аб,х'Вб,УВб,г^^

Численное решение каждой из сформированных систем нелинейных уравнений позволит определить 7 подлежащих уточнению параметров модели МПКЦ: длину одной штанги и координаты соединяемых ею шарниров.

Необходимость в многократном измерении координат (x_Sk,y_s , z_Sk), к = 1,3 с целью определения значений текущих выходных координат требует внесения в этот процесс элементов автоматизации. В частности, в метрологическую оснастку могут быть встроены датчики, способные регистрировать изменения ее пространственной ориентации относительно начального состояния. В этом случае возможно существенное ускорение процесса получения информации, необходимой для проведения идентификации модели МПКЦ.