Параметрическая идентификация нелинейно вязких свойств жидкостей вибрационным методом затухающих колебаний

Неньютоновские жидкости являются основными рабочими средами в разнообразных технологических процессах. Сложные реологические свойства смазок, масел и других нефтепродуктов зачастую существенно влияют на их поведение в условиях эксплуатации, а корректные физически обоснованные оценки свойств позволяют обеспечивать нормальные и надежные режимы функционирования. Большинство экспериментов по изучению реологических свойств таких труднодоступных для исследования сред как, например, высокотемпературные и химически агрессивные жидкости, интерпретировано в предположении о ньютоновском характере их течения, что может приводить к противоречиям в величине вязкости и характере ее зависимости от термодинамических параметров. Ранее авторами [1] были изучены возможности наблюдения неньютоновских свойств в экспериментах с крутильным вискозиметром. Другим таким методом является вибрационный [2], в котором о реологических свойствах жидкости судят по параметрам вынужденных колебаний погруженной в эту среду пластины.

Помимо возможности работы с агрессивными средами, указанные выше нестационарные методы объединяют реализуемые в них условия, позволяющие сделать наблюдаемыми отдельные неньютоновские эффекты у жидкостей, обычно считающихся ньютоновскими, и решить задачу о реологической принадлежности среды. Так, для этих методов характерно изменение во времени приращений напряжений и деформаций, что делает возможным обнаружение, например, упругих свойств жидких сред или свойств текучих систем с переменным отношением между напряжением и скоростью сдвига. В режиме затухающих колебаний можно реализовать как предельно малые полные деформации, так и малые скорости деформаций, и обнаружить, в частности, слабопластичные свойства. К тому же, здесь вывод о реологической принадлежности среды делается на основе измерений параметров колебаний, которые могут быть выполнены с высокой точностью, недоступной для наблюдаемых параметров в других методиках.

Течения, возбуждаемые в неньютоновских средах осциллирующей в своей плоскости пластиной, уже давно привлекают внимание исследователей. Все эти работы, однако, посвящены решению несопряженной задачи, когда закон движения пластины задан, например, гармонической функцией времени, и относятся главным образом к вязкоупругим жидкостям: средам Олд-ройда-Б, Джонсона-Сигельмана, а также средам Ривлина-Эриксона 2-го, 3-го порядков и пр. (см., например, [3-5]). Методики же оценивания свойств неньютоновских сред вибрационным методом отсутствуют. К настоящему времени известны результаты, касающиеся, помимо ньютоновской, только простейших типов вязкоупругих сред, например, линейных, т.е. когда можно достаточно легко получить аналитическое выражение для закона колебаний пластины в регулярном установившемся режимах. Для неньютоновских сред этот закон в общем случае отличен от гармонического.

К тому же вибрационный метод развит для режима вынужденных колебаний. Возможность его использования в режиме свободных затухающих колебаний отмечена, в частности, в [2] в связи с измерением свойств ньютоновских сред с малыми вязкостями, но корректное обоснование расчетных соотношений отсутствует. В настоящей работе исследуем зависимость параметров колебаний от свойств среды для ньютоновских жидкостей, а также возможности метода затухающих колебаний по идентификации реологической принадлежности и свойств неньютоновских сред на примере нелинейно вязких со степенным реологическим законом.

Математическая формулировка задачи

Математическую модель вискозиметрических экспериментов представим в виде:

• 1)    уравнение движения пластины

dx

+ x =- F тр ,                                (1)

dT ²

• 2)    уравнение движения жидкости

  где

  
  

  ∂ U ₌ ∂ σ zx ∂ T    ∂ z ^,

  
  

  • 3)    начально-краевые условия для (1, 2)

  dx / dT_{T = 0} = 0, x (0) = x 0 , U ( z ,0) = 0, U (0, T ) = dx / dT , U ( ∞ , T ) = 0,

  • 4)    реологическое уравнение состояния

    • 4.1)    для ньютоновской среды

  
  

  σ zx ⁼

  
  

  • 4.2)    для нелинейно вязкой среды (по модели Оствальда–Вейля) m - 1

  
  

  σ zx ⁼

  
  

  ^,

  
  

  b = ω ₀ ^{m - 1} K_v /( v ρ ) , x = x / d , T = ω ₀ t , λ = ω ₀ / ω , ω ₀ ² = k / m ₀, z = z / d , d = v / ω ₀ , A = Sd ρ / m ₀, U = V /( d ω ₀),

  
  
  
  

σzx – zx-я компонента тензора напряжений, Fтр =-2Aσzx   – действующая на пластину сила z=0

трения, V= Vx – скорость колеблющейся пластины, d – толщина пограничного слоя, m и Kv – показатель и постоянная степенного реологического закона, S – площадь поверхности пластины, m0 – масса подвесной системы, t – время, ν – кинематическая вязкость, ρ – плотность, x – линейное смещение пластины, x0 – начальное смещение, k – жесткость пружины; ось Z ортогональна плоскости пластины, z = 0 – на пластине; система (1)–(3), (5) решается численно; затуханием колебаний в отсутствие среды и краевыми эффектами пренебрегаем.

Результаты и обсуждение

Ньютоновские среды

Сначала рассмотрим частный случай ньютоновской среды, когда b=m=1. Разыскивая закон колебаний пластины в виде x =x0 exp[-iT(θ- ∆i)] ,                                     (7)

из решения системы (1)–(4) найдем зависимость для определения параметров колебаний

[ 1 - ( 0 -A i )² ] - 2 A^fi ( 0 -A i )³ / ² = 0,                             (8)

где θ = ω / ω ₀ = 1/ λ , ∆ = ( δ /(2 π )) ⋅ ω / ω ₀ – коэффициент затухания, δ – логарифмический декремент затухания колебаний, ω = 2 π / τ и ω ₀ = 2 π / τ ₀ – частоты колебаний пластины с жидкостью и без нее, τ и τ ₀ – соответствующие периоды колебаний, i =- 1 .

Расчет и конструирование

Для ньютоновской среды параметры колебаний 6 и А не зависят от начальной амплитуды колебаний x о и определяются одним параметром A (рис. 1). Высокие значения 5 ограничивают интервал целесообразных значений A , например, до A <  0.1.

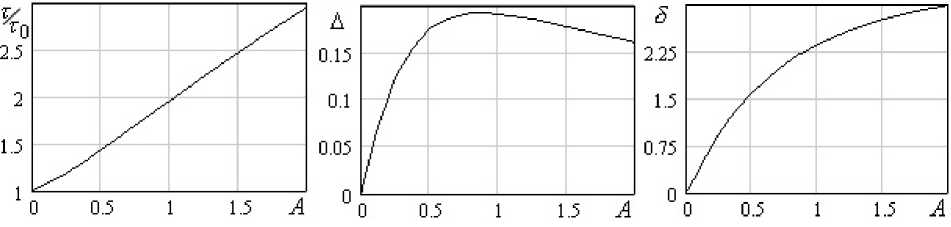
Рис. 1. Зависимость параметров колебаний от условий эксперимента для ньютоновских сред

Нелинейно вязкие среды

Установившиеся колебания пластины, погруженной в ньютоновскую жидкость, являются изосинхронными. Для неньютоновских сред возможно нарушение подобного асимптотического режима. В дальнейшем под периодом колебаний будем понимать величину т = 2 А Т _т , где А Т _т -разность между двумя соседними моментами времени, когда x обращается в нуль, а декремент затухания определим как 5 = 2ln| x i / x 2] , где x i , x 2 - соседние экстремальные значения x ⁽| ^x 1| > | ^x 2| )-

Зависимость поведения параметров колебаний от времени, т.е. от номера колебания N , при различных условиях эксперимента и свойствах среды продемонстрирована на рис. 2, 3 при x 0 = 1. Видно, что для жидкостей с m >  1 значения периода и декремента затухания падают в процессе колебаний, а для жидкостей с m <  1 - растут. Эти качественные особенности можно пояснить следующим образом. Согласно вискозиметрическому уравнению (8) для m = 1 значения X и 5 растут с ростом A . Для нелинейно вязкой среды в качестве параметра A может принять А _нв = A^bD m ^{- 1} , где D = |д U /д z | — второй инвариант тензора скоростей деформации. В процессе колебаний усредненное по полупериоду значение D падает, и кажущаяся вязкость bD^{m - 1} уменьшается, т.е. значение A _нв для дилатантных сред ( m >  1) падает, а для псевдопластичных ( m <  1) - растет. Соответствующим образом с течением времени изменяются и параметры коле-

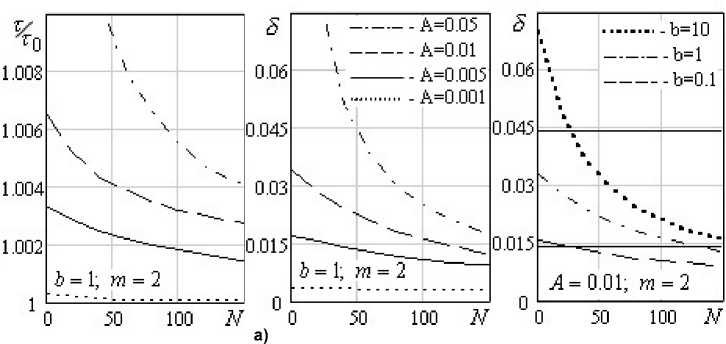
Рис. 2. Изменение параметров колебаний в процессе их затухания при различных значениях параметров А (а) и b (б)

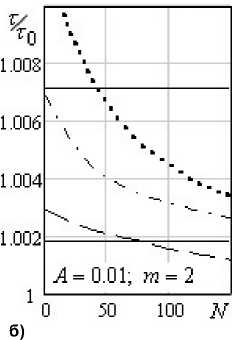
баний т и 5 . Для m = 1 значение A _нв, а, следовательно, и значения т , 5 , остаются постоянными в процессе колебаний. Напомним, что зависимость (8) не учитывает переходные процессы, описывая регулярный режим колебаний. Для ньютоновской жидкости при b ^ 1 параметры колебаний определялись из (8) с учетом соотношений для b и A (6).

Горизонтальные линии на рис. 2б, 3 соответствуют аналитическому решению для ньютоновской среды (при b = 1 - верхняя линия и при b = 0.1 - нижняя линия на рис. 2б). При b = 1 кривые т = т ( N ) при одном и том же т ₀ и различных m стремятся при N ^ 1 к одному значению т . Это позволяет определить A из зависимости (8) как при m = 1 и оценить K v в предположении b = 1. При b <  1 значения параметров колебаний при N ^ 1 для нелинейно вязких сред выше,

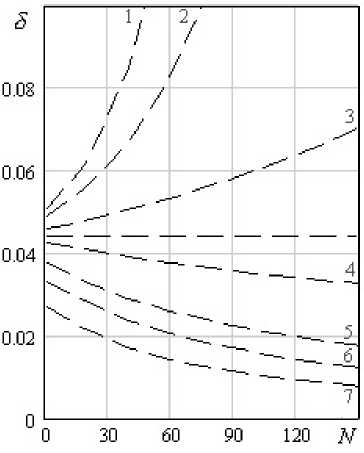
Рис. 3. Изменение параметров колебаний в процессе их затухания при различных показателях степенного реологического закона b = 1, A = 0,01;

1 – m = 2/3; 2 – m = 3/4; 3 – m = 0,9; 4 – m = 1,1;

5 – m = 3/2; 6 – m = 2; 7 – m = 3

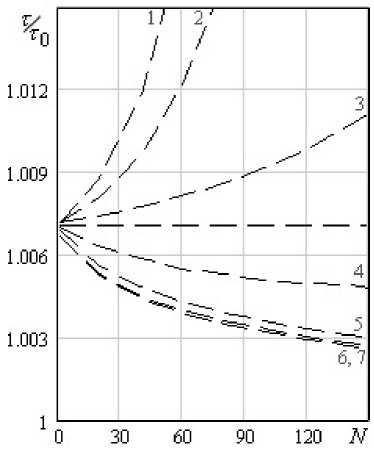
чем для ньютоновской жидкости, а при b >  1 - ниже (для параметров рис. 2б при b = 10 из (8) для ньютоновской среды получаем 5 ~ 0,137 и т / т ₀ ~ 1,0225).

Показатель степенного реологического закона можно найти из исследования асимптотических значений 5 и т / т ₀ при N ^^ (в частности, можно принять N = 150), когда изменение параметров колебаний во времени уже мало и не вносит значительной ошибки ввиду недостаточной точности измерения их на практике для отдельного колебания. Этот способ подробнее был обсужден на примере крутильно-колебательного вискозиметра (см., например, [6]). Дополнительный способ оценивания реологических свойств среды вибрационным методом по сравнению, например, с аналогичным в этом отношении крутильно-колебательным методом, основан на изучении зависимости поведения параметров колебаний от времени при различных начальных амплитудах колебаний x 0 . Повторим, что для ньютоновской среды 6 и 5 в установившемся регулярном режиме колебаний при различных x 0 и заданном A одинаковы.

Ниже подробнее остановимся на одном из способов предварительной оценки b и m по значениям 2 1 = у 6 n ^ 1 и 5 1 = 5 n ^ 1 для сред с m >  1. Кривые, демонстрирующие изменение 2 1 и 5 1 в зависимости от свойств среды, приведены на рис. 4 и построены с учетом переходных процессов, реализуемых при начальных условиях (3). Характер поведения параметров колебаний в зависимости от m при различных x 0 определяется типом среды при этих условиях, и, в частности, величиной эффективной вязкости, зависящей от модуля скорости сдвига. Выполняя эксперименты при фиксированном значении A = 0.01, по рис. 4 можно оценить b и m .

Расчет и конструирование

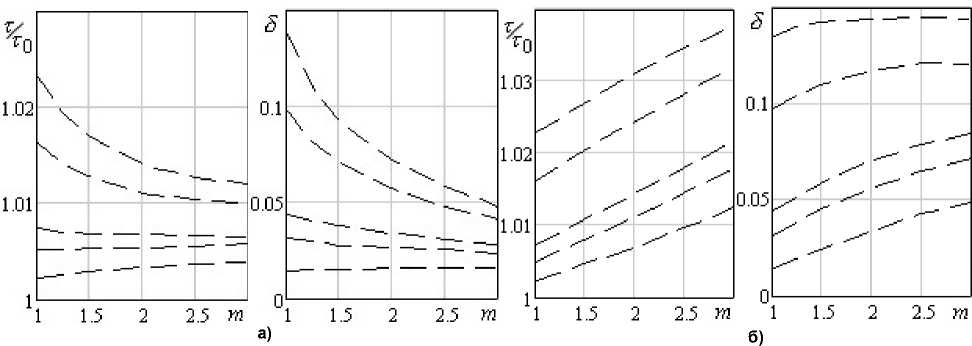
Рис. 4. Параметры колебаний X 1 и 8 1 при различных свойствах среды А = 0,01; X ₀ = 1 (а) и X ₀ = 10 (б); кривые: сверху вниз b = 10; 5; 1; 0,5; 0,1

Полученные значения b и m необходимо уточнить путем сравнения полных зависимостей параметров колебаний от времени в процессе колебаний 8 = 8 (N ) и X = X (N ), т.е. путем минимизации функции качества, являющейся критерием соответствия экспериментальных и расчетных данных, построенной, например, по методу наименьших квадратов:

N

f ⁽ m , b ) = Е⁽ y pi ^- У э1 ^{) 2 ,                                   (9)}

i = 1

где y_pl и y_эl – расчетные и экспериментальные значения измеряемых в эксперименте величин (т.е. 8 и т / т ₀), l - номера экспериментальных точек. Функция (9) имеет криволинейный овраг на плоскости ( m , b ), и поэтому необходимо использовать овражные методы поиска, имеющие нелокальный характер. В общем случае можно принять вектор y = x , т.е. рассматривать соответствие экспериментального и расчетного закона колебаний. Для повышения точности измерения нелинейных свойств выбор оптимальных параметров колебаний (и установки) определяется из условия

N

Е \( d y i / d b ) + ( д y i / д m ) ^ max,                        (10)

l = 1

и при равенстве дисперсий в различных экспериментальных точках берется максимально возможное число точек замера.

Заключение

Итак, в настоящей работе

• 1)    для ньютоновских сред для режима установившихся колебаний построено вискозиметри-ческое уравнение, связывающее вязкость жидкости с измеряемыми в эксперименте параметрами: периодом и декрементом затухания колебаний;

• 2)    обсуждено решение проблемы идентификации реологической принадлежности жидкостей как нелинейно вязких со степенным реологическим законом на примере модели Оствальда– Вейля. В условиях, свойственных вибрационному методу затухающих колебаний, выявлены эффекты, связанные с таким поведением среды;

• 3)    предложен один из возможных способов оценивания неизвестных реологических свойств нелинейно вязких сред по наблюдаемым в эксперименте периоду и декременту затухания колебаний.